Axiomes de la théorie des ensembles

Pour quoi faire ?

Quiconque a eu un jour affaire à un enfant en âge de formuler des questions commençant par "Pourquoi ?" le sait: au bout d'un moment, la seule réponse valide est "Parce que c'est comme ça". Si on espère faire quelque chose de sa journée, certaines choses doivent être acceptées comme vraies, l'aternative étant la descente dans la spirale infernale de la régression infinie. Les mathématiciens, en particulier, passent leurs journées à faire des déductions; mais on déduit quelque chose de quelque chose d'autre, et pas de rien ! Il faut donc se mettre d'accord sur un certain nombre, aussi faible que possible, de choses vraies sans discussion. Afin de mieux faire passer la pilule, on essaie de les choisir aussi évidentes que possible; par exemple, non(non($A)) \Rightarrow A$ est un axiome de la logique propositionnelle classique (encore que certains y trouvent quelque chose à redire !) Un exemple de système d'axiomes est celui des Éléments d'Euclide: cinq propriétés "évidentes" des droites, points et cercles servent de base au reste de cet édifice de la géométrie.

Au XIXème siècle, une série de percées dans tous les domaines des mathématiques ont mis en évidence une autre raison de formaliser les axiomes d'un domaine: cela permet d'isoler les propriétés que l'on veut étudier, et d'obtenir des résultats d'une grande généralité. Par exemple, il existe plusieurs façons de mesurer des distances: la distance sur un plan, qu'on utilise à "petite" échelle, ne sera pas la même que la distance sur une sphère utilisée par les avions (illustation ici et là); la distance "à vol d'oiseau" n'est pas la même que celle qui suit la route. Qu'entend-on alors par "la distance" ? On peut tenter d'extraire les propriétés communes: une distance est une fonction $d$ qui mange deux points de l'espace $p$ et $q$ et renvoie un nombre positif. En jargon: $$d: E \times E \rightarrow \mathbb R^+, (p,q) \mapsto d(p,q) \geq 0$$ Si $p$ et $q$ sont le même point, alors ils sont certainement à distance zéro. Et réciproquement: si on peut passer de $p$ à $q$ en parcourant une distance de zéro, c'est qu'ils sont au même endroit! $$d(p,q)=0 \Leftrightarrow p=q$$ De plus, même si on n'en a pas l'impression, le trajet retour nous fait parcourir la même distance que l'aller: $$d(p,q) = d(q,p)$$ Enfin, un détour par la poste (disons, par un troisième point $e$) rallonge le trajet, ou au mieux ne le change pas (si c'est sur la route!) mais n'a aucune chance de le raccourcir: $$d(p,q) \leq d(p,e) + d(e,q).$$ En mathématiques, on appellera distance toute fonction $d$ ayant ces trois propriétés (ou axiomes), et tout ce qu'on prouvera sur une telle fonction s'appliquera aussi bien au trajet des piétons qu'à ceux des navettes spatiales.

Les ensembles sont parmi les objets les plus simples et fondamentaux qui soient en mathématiques. Ce post décrit le système d'axiomes le plus commun pour jouer avec: l'axiomatique de Zermelo-Fraenkel avec axiome du Choix, ou ZFC. Elle inclut:

• L'axiome d'extensionnalité
• Le schéma d'axiome de compréhension
• L'axiome d'existence
• L'axiome de la paire
• L'axiome de l'union
• L'axiome de l'ensemble des parties
• L'axiome de l'infini
• Les axiomes de fondation et de remplacement
• L'axiome du choix

Avant de les détailler, parlons un peu du contexte qui les a rendus indispensables.

La (douloureuse) naissance de la théorie des ensembles

Les ensembles sont considérés comme les briques de base des mathématiques; on peut tout reconstruire à partir d'eux seuls. A la fin du XIX siècle, dans un effort pour trouver le fondements ultime des mathématiques, Cantor (entre autres) développe la théorie des ensembles; ou plutôt, ce que l'on appelle avec le recul et non sans un certain mépris, la théorie naïve des ensembles. Cette première version, exprimée en langage courant, et basée sur d'apparentes évidences, permit de grandes avancées notamment dans la compréhension de l'infini...avant de se casser les dents sur des paradoxes, laissant entendre que la théorie était contradictoire (la pire insulte mathématique!). Par exemple, le paradoxe du plus grand cardinal, le paradoxe de Berry, ou encore le fameux paradoxe du barbier dont on reparlera plus loin.

Il y eut deux réactions à ces paradoxes: le rejet, par les intuitionnistes menés par Brouwer, qui militaient pour le retour des maths à des constructions finies ("Il n'y a pas d'infini; les Cantoriens l'ont oublié, et sont tombés dans la contradiction" - Poincaré); et le déni ("Nul ne nous chassera du paradis que Cantor a créé pour nous." - Hilbert). Pour dépasser la controverse, en tout cas, il apparut nécessaire de formaliser la théorie des ensembles, et d'en assurer la cohérence: c'est le rôle des systèmes axiomatiques. Il en existe plusieurs, mais le plus connu est le système de Zermelo-Fraenkel, et c'est celui dont on va discuter.

Essayons donc le même raisonnement qui marche si bien pour les distances. Qu'est-ce qu'un ensemble, et que nous sentons-nous en droit d'exiger ?

Un ensemble, pour le dire sans détour, c'est "un tas de trucs", sans propriété particulière, ce que l'on souligne en dessinant les ensembles comme des patatoïdes informes. Pour faire plus distingué, nous dirons que les "trucs" sont les éléments de l'ensemble. Un élément $a$ peut appartenir à un ensemble $A$, et on notera alors $$a\in A.$$ Deux ensembles $A$ et $B$ peuvent être égaux: $$A=B$$.

Et c'est tout.

Cela peut sembler un peu sec, mais on va voir que cela suffit. Que peut-on tirer de tout ceci ?

Premier jour: l'axiome d'extensionnalité

Au commencement, ce que l'on sait sur un ensemble, c'est qu'il contient des éléments, on s'attend à ce qu'un ensemble soit caractérisé par ses éléments; autrement dit, deux ensembles sont égaux si, et seulement si, ils contiennent les mêmes éléments. En jargon:

$$\color{blue}{\forall A \forall B (\forall x(x \in A \Leftrightarrow x \in B) \Leftrightarrow A=B)}$$

Ceci permet d'enfoncer quelques portes ouvertes; par exemple, les ensembles $\{a,a,b\}$ et $\{a,b\}$ sont les mêmes.

Une autre remarque porte sur l'utilisation du quantificateur $\forall$. On est plus habitué à ce qu'il soit utilisé sous la forme $\forall x \in E$, où $E$ est un ensemble donné (par exemple, $]0,1[$). Mais justement, ici, aucun ensemble n'est donné, puisqu'on ne les a pas encore reconstruits! On a donc des $\forall$ qui flottent dans le vide. Et, même si l'usage de majuscules et de minuscules enfume l'intuition avec succès, le "même" $\forall$ s'applique à $A$, $B$ et $x$: ils sont tous de la même nature, ce sont tous des ensembles. Oui, même $x$! Tous les objets que l'on s'autorise ici sont des ensembles, et donc, les éléments des ensembles sont eux-même des ensembles.

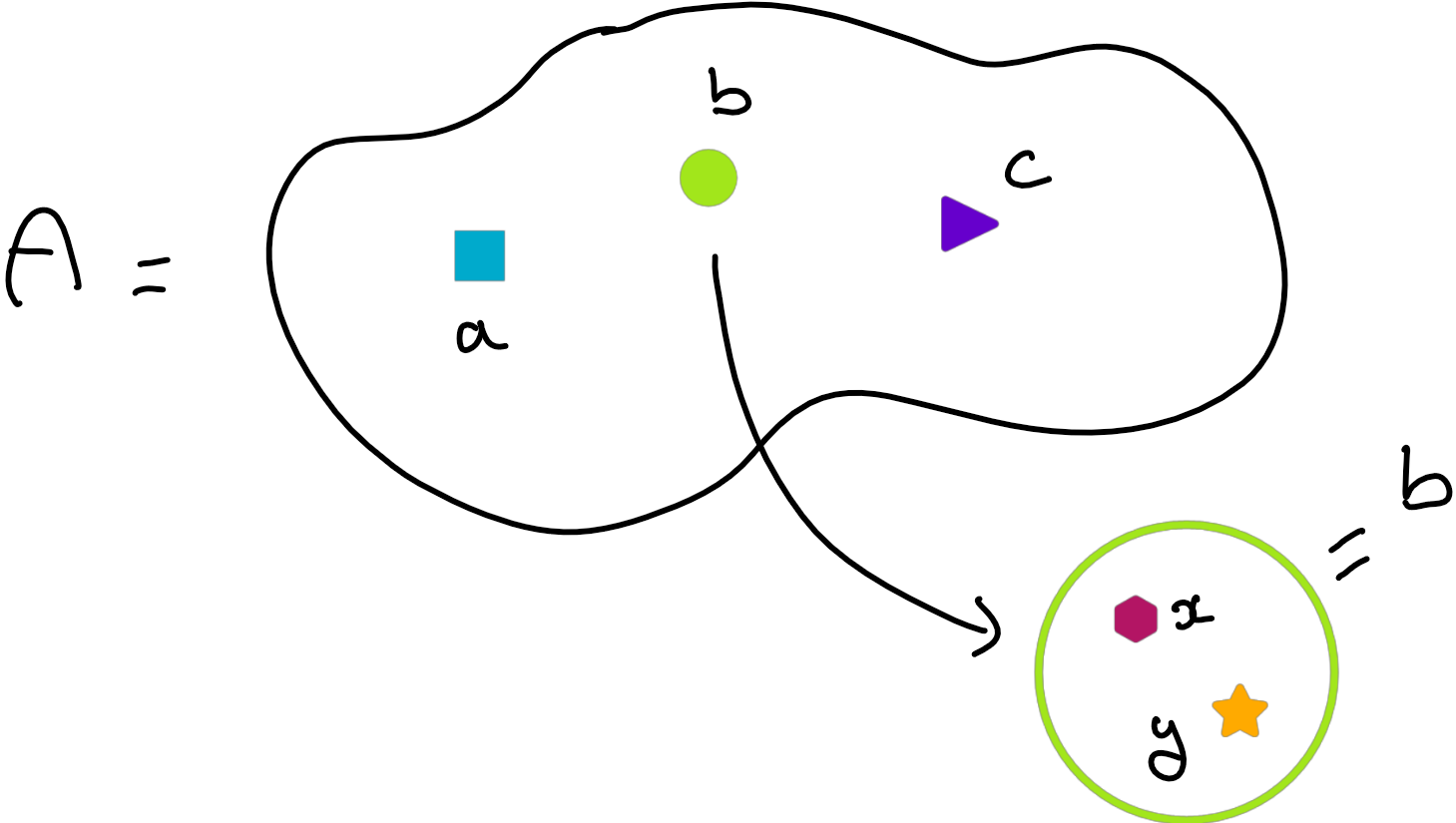
Il faut donc être attentif à la différence entre $x\in A$ ("l'ensemble $x$ est un élément de l'ensemble $A$") et la relation plus habituelle $x \subset A$ ("l'ensemble $x$ est un sous-ensemble de l'ensemble A"); la première relation est la brique de base de notre théorie; la deuxième est définie par "tout élément de $x$ est aussi un élément de A":

$$x\subset A \Leftrightarrow \forall y\,(y\in x \Rightarrow y \in A).$$

Ainsi la définition de l'égalité entre deux ensembles fut clarifiée par l'axiome d'extensionnalité, et Dieu vit que cela était bon. Il y eut un soir et il y eut un matin: ce fut le premier axiome.

Deuxième jour: Axiome de compréhension

Pour beaucoup d'ensembles plus intéressants que $\{a,b,c\}$ ou $\{$Papaye, Motörhead, Matrix Reloaded$\}$, par exemple l'ensemble des entiers pairs, ou des réels non rationnels, énumérer tous les éléments est chronophage et peu écologique. On les présente donc plutôt comme ceci:

$$\{n\in \mathbb{N},\ \exists p \in \mathbb N,\, n=2p\},\ \{x \in \mathbb{R}, x \notin \mathbb Q\}$$

En d'autre termes, on caractérise ces ensembles via une propriété que vérifient leurs éléments. L'axiome de compréhension a pour rôle de nous autoriser à faire ça: si $\phi$ est une formule du langage de la théorie des ensembles (c'est à dire une phrase raisonnable formée à partir de $\in$, $=$ et des connecteurs logiques comme et, ou, non, $\forall$...), et si $A$ est un ensemble, alors il existe un ensemble formé des éléments de $A$ qui vérifient $\phi$. En hiéroglyphes:

$$\color{blue}{\forall A\, \exists B\,(x \in B \Leftrightarrow ((x\in A)\,\text{ et } \phi))}$$

On parle en fait de schéma d'axiomes: pour chaque formule $\phi$, on a un axiome qui nous donne le droit de construire le sous-ensemble correspondant. Pour en savoir plus sur les formules, consulter par exemple la première partie de ce document.

Mais au fait, pourquoi un sous-ensemble ? Pourquoi ne pas simplement se donner le droit, somme toute assez naturel, de construire l'ensemble de tout ce qui vérifie une certaine propriété ?

C'est en fait ce que Cantor a fait: sa théorie incluait un axiome de compréhension non restreint, où l'on se dispense de l'ensemble $A$.

$$\exists B\,(x \in B \Leftrightarrow \phi)$$

C'est alors que Russell arrive avec son rasoir et égorge la théorie. En effet, la théorie de Cantor l'autorise à définir (accrochez-vous) l'ensemble $V$ de nous les ensembles qui ne se contiennent pas eux-mêmes (rappelons que les éléments des ensembles sont aussi des ensembles, donc un ensemble pourrait, a priori, être un élément de lui-même):

$$V = \{x,\ x\notin x\}$$

Ensuite, Russell porte sa pipe à sa bouche d'un air suffisant et demande: est-ce que $V$ se contient lui-même ? Une façon classique de présenter le problème est:

Dans cette ville, le barbier ne rase que les hommes qui ne se rasent pas eux-mêmes. Est-ce que le barbier se rase lui-même ?

Et là, c'est le paradoxe: $V$ se contient lui-même si, et seulement si, $V$ ne se contient pas lui-même: la théorie est contradictoire.

Comment l'ensemble $A$ nous sauve-t-il de l'apocalypse ? Notre axiome restreint de compréhension nous permet de former l'ensemble

$$V = \{x\in A,\, x\notin x\}$$

En particulier, $V\in V$ si et seulement si $V \in A$ et $V\notin V$. Donc, soit $V\in A$ et on retombe sur une contradiction, ou alors $V \notin A$ et tout va bien; donc $V\notin A$.

Une conséquence intéressante de ce sauvetage est que, quel que soit l'ensemble $A$, il y a un ensemble $V$ qui existe d'après l'axiome de compréhension, mais qui n'est pas dans $A$. Donc, il n'y a pas d'"ensemble de tous les ensembles", ou, pour le dire de façon spectaculaire: Il n'y a pas d'univers (où l'on entend "univers" au sens d'univers du discours, comme expliqué dans la troisième partie de ce document).

L'axiome restreint n'est pas la seule façon de contourner le redoutable paradoxe du barbier: Russell et Whitehead, dans Principia Mathematica, mettent sur pied la théorie des types, qui hiérarchise les objets: il existe des éléments primitifs, dits de type 0; les objets qui contiennent des objets de type 0 sont de type 1, ceux qui contiennent des objets de type 1 sont de typer 2, etc. Ce système interdit le type d'autoréférence qui donne lieu au paradoxe. Le concept de classe du système d'axiomes NGB (Neumann-Gödel-Bernays) permet aussi d'éviter le désastre.

Ainsi le schéma d'axiomes de compréhension nous permet de définir des ensembles sans avoir à spécifier chaque élément et sans être assassinés par un barbier fou; et Dieu, soulagé, vit que cela était bon. Il y eut un soir et il y eut un matin: ce fut le deuxième axiome.

Troisième jour: Axiome d'existence

Le troisième jour, Dieu s'éveilla avec un doute affreux: existe-t-il ne serait-ce qu'un ensemble ? Les deux axiomes précédents permettent, respectivement, de spécifier quand deux ensembles sont égaux, et de construire des sous-ensembles à partir d'un ensemble donné, mais tout ceci perd de son intérêt s'il n'y a pas d'ensembles du tout. Ainsi, le troisième axiome garantit qu'on ne construit pas une théorie de rien: il dit qu'il existe un ensemble, disons $O$.

Muni de l'axiome de compréhension, on peut alors construire un ensemble en apparence peu intéressant, mais en fait d'une importance cruciale (un peu comme zéro): l'ensemble vide

$$\emptyset = \{x\in O; x \neq x\}$$

L'ensemble vide est un sous-ensemble de tout ensemble $A$; si ce n'était pas le cas, il y aurait un élément $x$ de $\emptyset$ tel que $x\notin A$. Mais pour ça, encore faudrait-il qu'il y ait un élément dans $\emptyset$ !

Plus généralement, comme le disait un de mes professeurs de deuxième année, toute phrase qui commence par "Pour tout point de l'ensemble vide" est vraie. En effet, pour que "pour tout point de l'ensemble vide, truc" soit fausse, il faudrait qu'il y ait un élément de l'ensemble vide tel que truc soit faux. Mais justement, il n'y a rien dans $\emptyset$! Cela dit, j'ai essayé "Pour tout point de l'ensemble vide, j'ai un milliard d'euros", mais ça n'a pas marché.

Ainsi, la théorie des ensembles, non seulement ne parle pas dans le vide, mais permet de parler du vide. Après s'être fait une telle frayeur, Dieu décida de prendre le reste de la journée, et il vit que cela était bon. Il y eut un soir et il y eut un matin: ce fut le troisième axiome.

Quatrième jour: Axiome de la paire

Le quatrième jour, Dieu considéra sa théorie et la trouva un peu tristoune: un seul ensemble, probablement vide, et un moyen d'en sortir des sous-ensembles. Il décida donc de se donner quelques axiomes de construction, à commencer par cette idée simple: si j'ai un ensemble $A$, je peux trouver un deuxième ensemble dont $A$ est un élément. Non, mieux: si j'ai deux ensembles $A$ et $B$, je peux trouver un troisième ensemble $C$ dont les éléments sont exactement $A$ et $B$:

$$\color{blue}{\forall A\, \forall B\, \exists\, C(x \in C \Leftrightarrow (x=A \text{ ou } x=B))}$$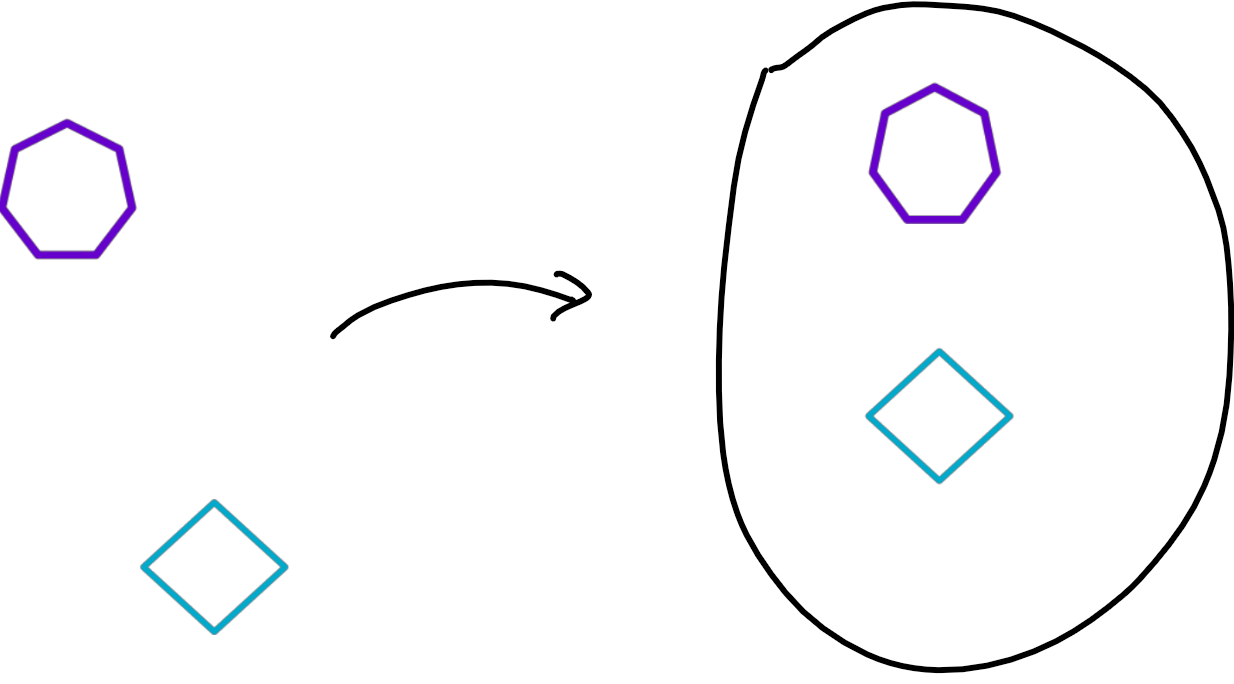

Attention, l'ensemble $C$ ainsi obtenu n'est pas l'union de $A$ et $B$ (ce sera l'objet de l'axiome suivant), mais l'ensemble à deux éléments $C=\{A, B\}$. $A$ et $B$ sont des éléments, et non des sous-ensembles de $C$ (toujours le même problème des ensembles qui sont des éléments d'autres ensembles!).

Avec cet axiome, si les ensembles $A$ et $B$ sont égaux, alors $C$ est le singleton $\{A\}$ (qui est différent de l'ensemble A, par la remarque ci-dessus). Donc, à partir de notre pauvre ensemble vide $\emptyset$, on obtient ainsi toute sortes de nouveaux ensembles:

$$\{\emptyset\}, \{\{\emptyset\}\}, \{\{\{\emptyset\}\}\}, \text{ mais aussi } \{\emptyset, \{\emptyset\}\}...$$

Cela n'a l'air de rien (c'est le cas de le dire), mais c'est ce qui nous permettra de reconstruire les entiers naturels.

On a ainsi obtenu toute une panoplie de nouveaux ensembles, et Dieu vit que cela était bon. Il y eut un soir et il y eut un matin: ce fut le quatrième axiome.

Cinquième jour: axiome de réunion

L'axiome de la paire nous permet, entre autres, de rajouter autant d'accolades que l'on souhaite autour d'ensembles, et de les transfomer en élément d'un ensemble plus gros. Mais, puisque les éléments des ensembles sont eux-même des ensembles, il paraîtrait naturel de réaliser l'opération inverse: prendre un ensemble A, et pour chaque élément $a$ de $A$, extraire les éléments de $a$ et les déverser dans un nouvel ensemble $D$, que l'on notera $\bigcup A$. Il nous faudrait un axiome de "dépaquetage", en somme. En sumérien archaïque:

$$\color{blue}{\forall A\, \exists D\, \forall x\,(x\in D \Leftrightarrow \exists a(x\in a \text{ et } a\in A))}$$

En particulier, si l'on applique ça à la paire $\{A,B\}$ obtenue par l'axiome...de la paire, on obtient un ensemble qui contient les éléments de $A$ et ceux de $B$: autrement dit, la réunion de $A$ et $B$ (d'où le nom axiome de la réunion, qui sonne plus professionnel que axiome de dépaquetage). On notera ce nouvel ensemble $A \cup B$.

On récupère alors les propriétés intuitives de l'union de deux ensembles, et le jargon qui les accompagne:

$$A \cup A = A \text{ (idempotence)}$$ $$A \cup B = B \cup A \text{ (commutativité)}$$ $$A \cup(B \cup C) = (A \cup B) \cup C \text{ (associativité)}$$ $$A \cup \emptyset = A \text{ (élément neutre)}$$

On pourrait s'attendre à ce que l'étape suivante soit un axiome d'intersection; mais en fait, on n'en a pas besoin. L'intersection de deux ensembles s'obtient directement à partir de l'axiome de compréhension:

$$A \cap B := \{x \in A,\, x\in B\}$$

où la formule $\phi$ est $x\in B$. On vérifie alors qu'on a toutes les propriétés usuelles

$$A \cap A = A$$ $$A \cap B = B \cap A $$ $$A \cap(B \cap C) = (A \cap B) \cap C $$ $$A \cap \emptyset = \emptyset$$

ainsi que les lois de distributivité

$$A \cap (B \cup C) = (A \cap B) \cup (A\cap C)$$ $$A \cup (B \cap C) = (A \cup B) \cap (A\cup C)$$

De manière générale, on a besoin d'axiomes quand on veut définir quelque chose de plus "gros" que le ou les ensembles dont on part: la paire, la réunion, etc. Les ensembles plus "petits" s'obtiennent en général à coup de compréhension. L'idée est que pour éviter le bazar lié à des monstres comme l'ensemble de tous les ensembles, on procède avec circonspection quand on veut s'agrandir.

Ainsi la théorie des ensembles commence à avoir la tête qu'on lui connaît, et Dieu vit que cela était bon. Il y eut un soir et il y eut un matin: ce fut le cinquième axiome.

Sixième jour: Axiome de l'ensemble des parties

Grâce à Russell, on a vu que l'ensemble de tous les ensembles n'existe pas dans notre théorie. Mais, avec plus de prudence, c'est-à-dire étant donné un ensemble $A$, qu'en est-il de l'ensemble des sous-ensembles de $A$, dont on ne cesse de parler ? L'axiome de l'ensemble des parties (mieux en anglais: "axiom of powers") garantit que cet ensemble existe, et on le note $\mathcal{P}(A)$. En hébreu traditionnel:

$$\color{blue}{\forall A\, \exists P\, \forall x\,(x\in P \Leftrightarrow x\subset A)}$$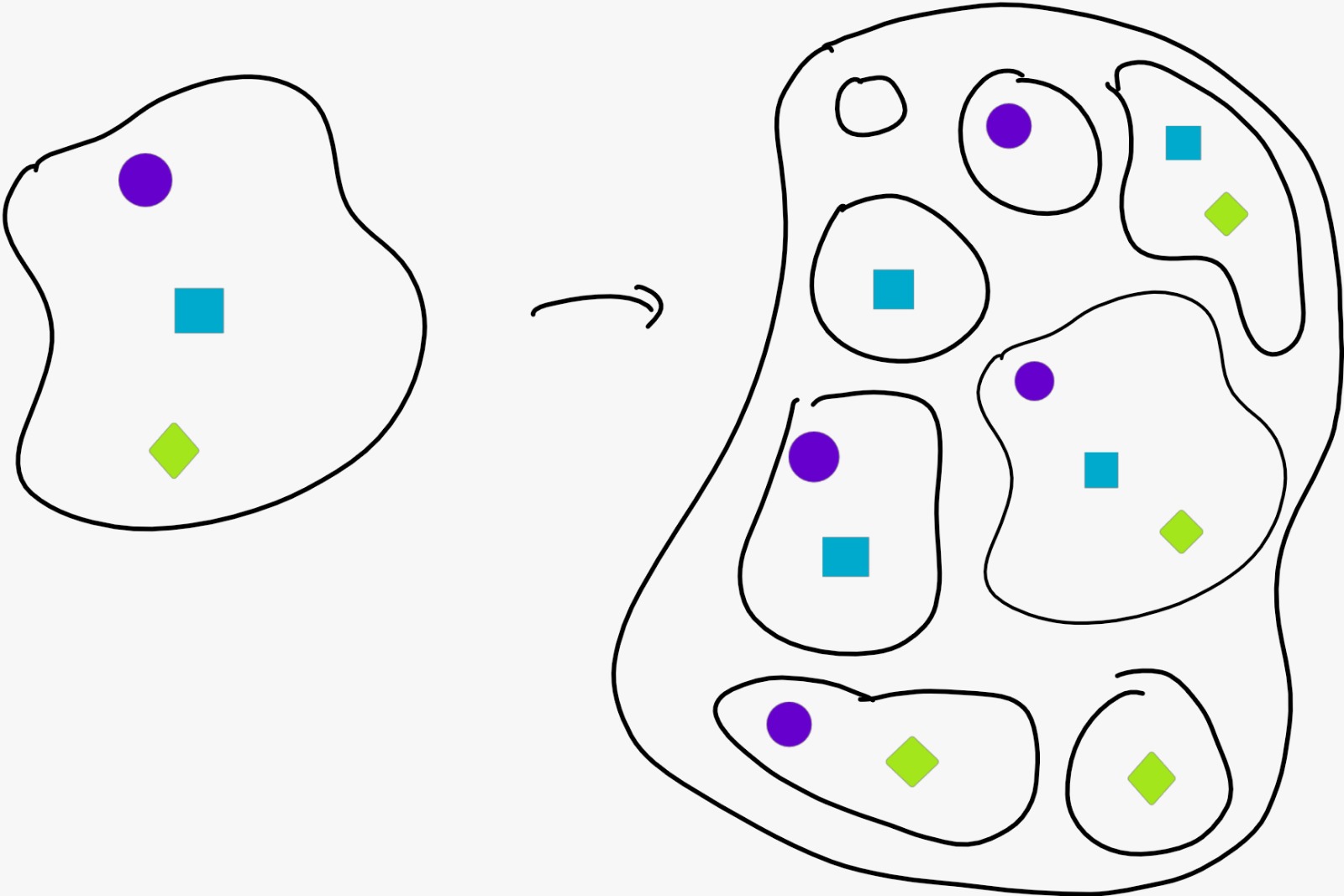

Ainsi,

$$\mathcal{P}(\emptyset)=\{\emptyset\},$$ $$\mathcal{P}(\{a\})=\{\emptyset, \{a\}\},$$ $$\mathcal{P}(\{a,b\})=\{\emptyset, \{a\}, \{b\}, \{a,b\}\}.$$

Nous n'avons pas encore discuté du nombre d'éléments d'un ensemble (ce que l'on appelle son cardinal), mais, en prenant un peu d'avance, on peut montrer que si $A$ a $n$ éléments, $\mathcal{P}(A)$ en a $2^n$ (d'où le nom "power set" pour $\mathcal P(A)$ en anglais, et la notation alternative $2^A$), et est donc beaucoup plus gros. Comme on le verra, ce commentaire devient particulièrement ébouriffant quand on parle d'ensembles infinis. Tiens, d'ailleurs...

Mais il se faisait tard, et on peut d'ores et déjà parler de tous les sous-ensembles d'un ensemble donné; et Dieu vit que cela était bon. Il y eut un soir et il y eut un matin: ce fut le sixième axiome.

Septième jour: Axiome de l'infini

Le septième jour, Dieu ne se reposa pas, car il avait le sentiment qu'il manquait quelque chose. Jusque-là, avec la seule brique de base de l'ensemble vide, en ajoutant moult accolades, on a vu qu'on pouvait construire toutes sortes de nouveaux ensembles. Mais si l'on veut qu'il reste un peu de temps dans la soirée, ce procédé doit finir un jour; en d'autre termes, et encore une fois, en anticipant sur notre discussion des cardinaux, on ne peut pour le moment parler que d'ensembles finis. Les mathématiciens ont tendance à se débarasser de ce genre de problème avec le très commode "..."; mais si l'on souhaite se donner une base solide pour les mathématiques, on ne peut se permettre ce genre d'artifice. Il nous faudrait donc, pour parler par exemple de $\mathbb{N}$ ou $\mathbb{R}$, un axiome garantissant l'existence d'au moins un ensemble infini.

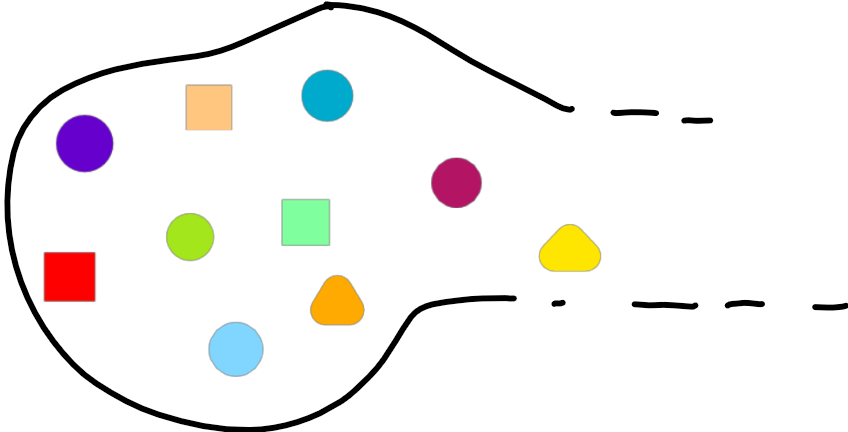
Mais encore faudrait-il savoir ce que l'on entend par là! Partons de cette idée des "...", ou encore "et ainsi de suite". Quelle est la "suite" ?

Partant d'un ensemble $x$, on va définir le successeur de $x$ par $x^+:= x \cup \{x\}$. (Devinette: quels axiomes a-t-on utilisés ?) Ainsi, en partant de notre brique de base $\emptyset$,

$$\emptyset^+ = \{\emptyset\}$$ $$ \{\emptyset\}^+=\{\emptyset, \{\emptyset\}\}$$ $$\{\emptyset, \{\emptyset\}\}^+= \{\emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\}\}\}$$

...et ainsi de suite (!). (Devinette: pourquoi sont-ils tous différents ?) On décrète alors qu'il existe un ensemble $I$ qui les contienne tous; c'est à dire qui contienne $\emptyset$ et tel que si $x\in I$ alors $x^+ \in I$. En patagonien appliqué:

$$\color{blue}{\exists I\, (\emptyset \in I \text{ et }\forall x\,(x\in I \Rightarrow x^+\in I))}$$

En fait, on vient, en douce, de décréter l'existence de $\mathbb{N}$. Mais on en reparlera.

Ainsi se termine la liste des axiomes de Zermelo, et Dieu vit que cela était bon. Il y eut un soir et il y eut un matin: ce fut le septième axiome.

Axiomes de Fraenkel

Ainsi, on est sur le point de pouvoir parler de nombres entiers: il semble qu'on soit parvenus à constuire les fondations de la maison des mathématiques (ou de l'hôtel de Hilbert), et que l'on peut entamer la construction du rez-de-chaussée avec sérénité. D'ailleurs, c'est exactement ce qu'a fait Zermelo.

Mais dans ZFC, il y a F, et c'est le F de Fraenkel, qui fit remarquer que la théorie de Zermelo ne permettait pas de traiter certaines questions ayant trait aux ensembles infinis (plus précisément, aux ordinaux, dont on reparlera quand on parlera d'infini). Il proposa donc l'ajout de deux axiomes supplémentaires: le schéma d'axiomes de remplacement et l'axiome de fondation (avec un nom pareil, comment s'en passer ?)

Le schéma d'axiomes de remplacement autorise une opération dont on n'a pas encore parlé, car on n'a pas encore construit les notions de relations et de fonction sur des ensembles, mais qui semble assez naturelle. Si on dispose d'une façon de transformer les éléments d'un ensemble en autre chose (par exemple, transformer $x$ en son successeur $x^+$), alors on souhaiterait pouvoir parler de l'ensemble de ces éléments "transformés". Encore plus généralement, si on a une formule $P(x,y)$ qui lie un unique objet $y$ à chaque élément $x$ d'un ensemble $A$, on aimerait que la collection de tous ces $y$ (en jargon: $\{y, \exists x(x\in A \text{ et } P(x,y)\}$) soit un ensemble. C'est ce que dit l'axiome de remplacement:

$$\color{blue}{\forall A\, \exists B\, \forall y\, (y\in B \Leftrightarrow (\exists x(x\in A \text{ et } P(x,y)))}$$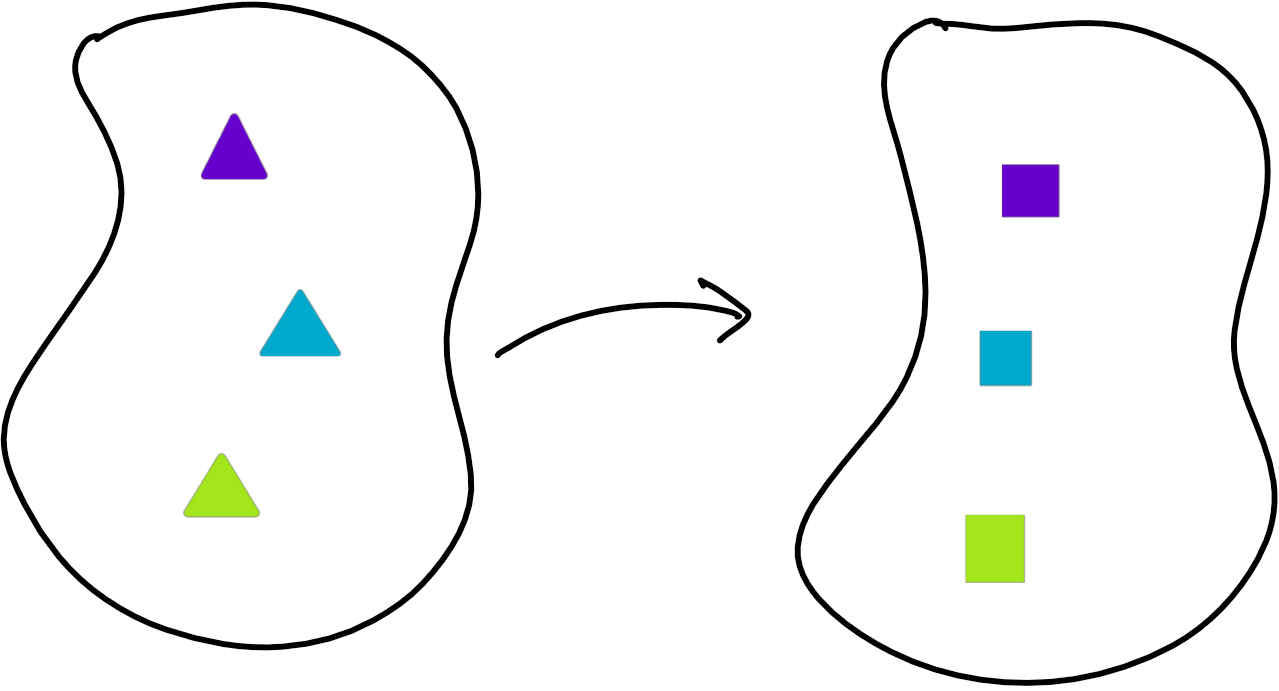

L'axiome de fondation, ou encore axiome de régularité, assure que si l'on prend un ensemble $A$, et que l'on prend un élément de $A$, et que l'on prend un élément de cet élément de $A$, et ainsi de suite...et bien justement, pas "et ainsi de suite": on veut qu'au bout d'un moment, ce procédé s'arrête. Autrement dit, on veut qu'il y ait un élément minimal pour l'appartenance sur $A$. Pour garantir cela, on demande que dans chaque ensemble non vide $A$, il y ait un élément $B$ qui ne contienne aucun élément de $A$; ainsi, si on "dépaquette" $B$, on ne risque pas de tourner en rond. En eldarin primitif:

$$\color{blue}{\forall A\, [A \neq \emptyset \Rightarrow \exists B\, (B\in A \text{ et }B \cap A = \emptyset)]}$$

Alors, on ne peut pas avoir de suite infinie $x_0 \ni x_1 \ni x_2\dots$; sinon, l'image de la transformation qui à $n$ associe $x_n$, qui est un ensemble par l'axiome de remplacement, contredirait l'axiome de fondation. Cet axiome permet aussi de tirer une deuxième fois dans le cadavre du paradoxe de Russell pour vérifier qu'il est bien mort: en effet, il interdit purement et simplement la relation $x\in x$, ce qui, franchement, épargne quantité de maux de crânes.

L'axiome du choix

Les plus observateurs remarqueront que dans ZFC, il y a aussi C: ce C vient de l'axiome du choix, un axiome d'apparence inoffensive mais dont les conséquences sont si étranges qu'elles méritent leur propre discussion (on parlera notamment de la façon de découper une orange pour en obtenir deux de même taille que la première, ou de comment utiliser l'axiome du choix pour commettre le crime parfait).

Cet axiome semble pourtant tout ce qu'il y a de raisonnable: si on a un ensemble $A$, ses éléments sont eux aussi des ensembles, et, s'ils sont tous non vides, l'axiome du choix donne le droit d'extraire un élément de chacun d'eux. On obtient ainsi une fonction de choix $C: A \rightarrow \bigcup A$. En Adûnaic occidental:

$$\color{blue}{\forall A\,[\emptyset\notin A \Rightarrow (\exists C: A \rightarrow \bigcup A, f(A)\in A)]}$$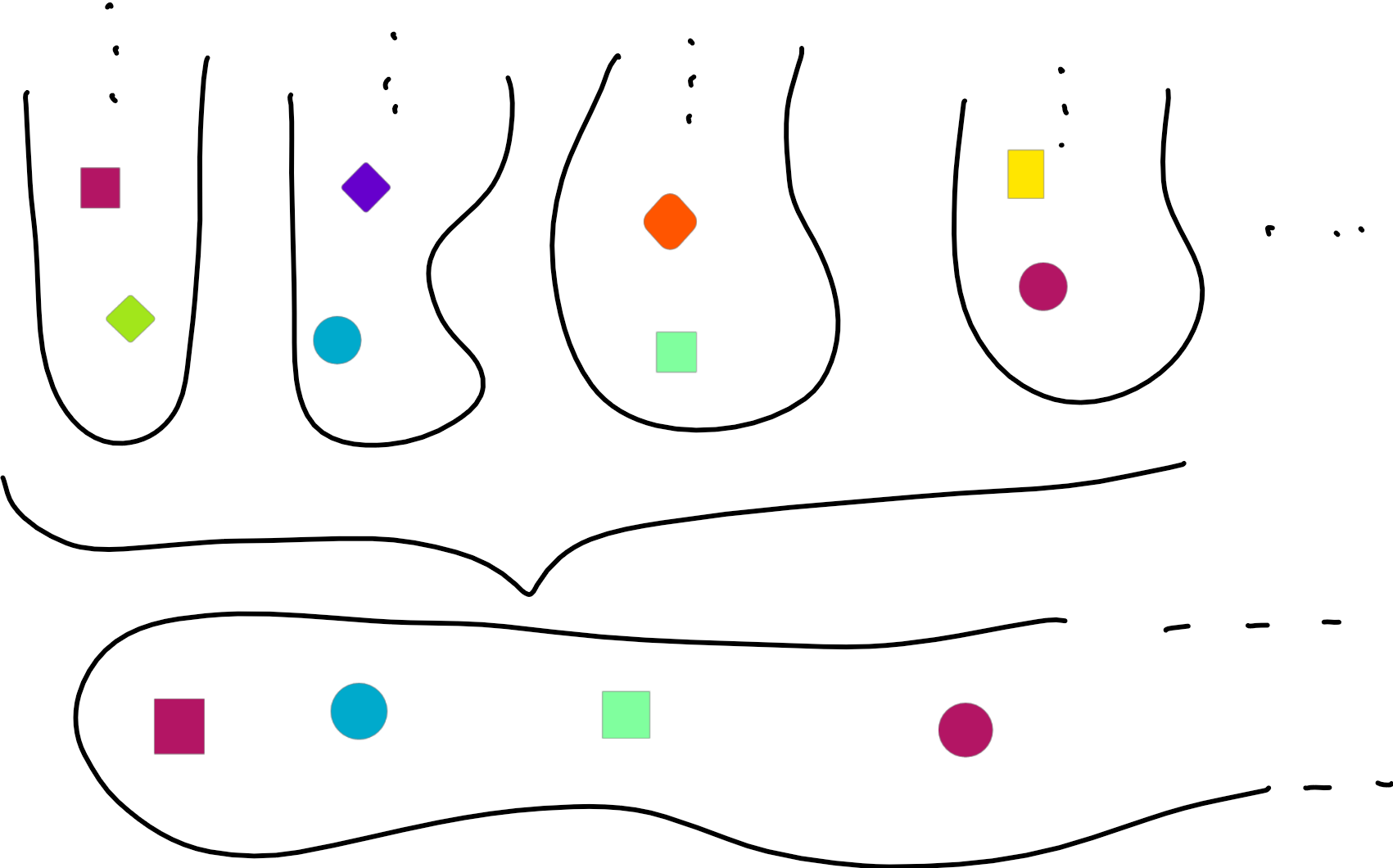

Conclusion

Avec les axiomes de ZFC, on arrive ainsi à traiter toutes les maths qu'on aurait raisonnablement envie de faire. De plus, les paradoxes qui pourrissaient la vie de Cantor ne se produisent pas dans ZFC: on l'a vu pour le paradoxe de Russell, et c'est aussi le cas pour les autres. On pourrait s'inquiéter de l'existence d'autres paradoxes, plus difficile à trouver; et en fait, Gödel a alimenté cette angoisse en montrant qu'on ne peut pas démontrer la cohérence d'un système d'axiome à l'intérieur de lui-même: autrement dit, on ne peut pas utiliser ZFC pour montrer ue ZFC est cohérent. Cependant, les experts pensent que s'il y avait des contradictions dans ZFC, on les aurait vu depuis, que diable; et des résultats encourageants sur l'indépendance des différents axiomes entre eux ont été obtenus, garantissant qu'ils ne se contredisent pas entre eux (cela dit, comme le montre l'axiome de compréhension non restreint de Cantor, un seul axiome peut suffire à déclencher le chaos).