Construire le temps
Continuum constructif et physique fondamentale.
Dans un épisode précédent, on a discuté des mathématiques constructives, mises au point par l'irascible Brouwer pour éliminer les contradictions des mathématiques "classiques", dues, selon lui, à l'infâme loi du Tiers Exclus.
Plus récemment (en fait, très récemment), le physicien suisse Nicolas Gisin a avancé l'idée que les maths constructives de Brouwer seraient plus adaptées que les maths habituelles pour représenter la réalité en physique fondamentale. Notamment, le passage du temps, et le déterminisme.
Relativité et univers-bloc
Commençons par le temps. Depuis Einstein (un type qui a souvent eu raison), on considère généralement que le bon cadre pour faire de la physique est, non pas juste l'espace, mais l'espace-temps, que l'on peut représenter comme ceci:
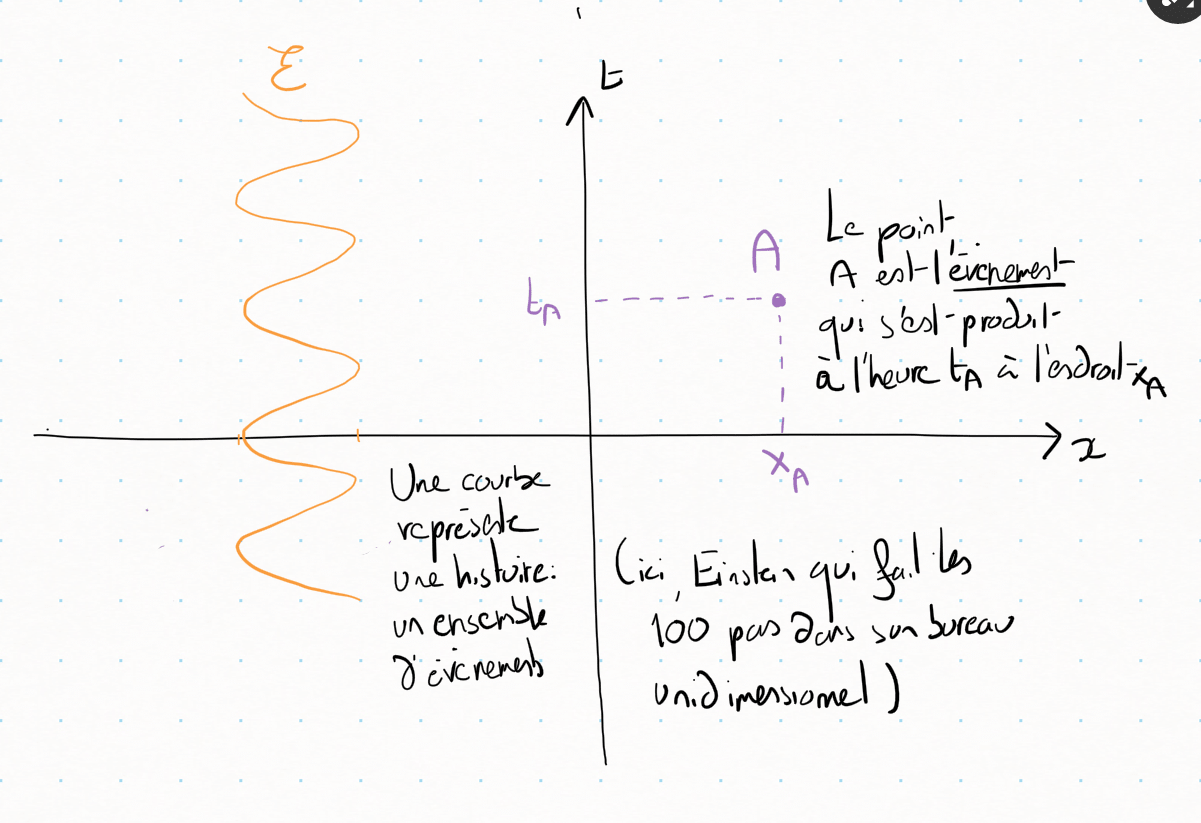
Dans cet exemple, il n'y a qu'une dimension d'espace: on ne peut se déplacer que dans une direction (c'est un espace-temps un peu limité), et avancer dans le temps. Chaque point $(x,t)$ représente un évènement (ce qui se passe à l'endroit $x$ à l'instant $t$), et non une position dans un plan. Une ligne horizontale tracée à $t=$ 28 mai 2020, 17h, représente ainsi l'entièreté de l'espace à l'heure du thé aujourd'hui.
La courbe orange représente l'histoire d'Albert (sa ligne d'univers, en plus classe), qui fait des allers-retour de gauche à droite tout en avançant dans le temps, ce qui nous donne cette forme en S.

Ci-dessus, un espace-temps à deux dimensions d'espace: il se présente comme une miche de pain, dont chaque tranche représente la totalité de l'espace à un instant donné $t$ (cette analogie est plagiée sans vergogne sur Brian Greene, dont je ne saurais trop recommander les livres).
L'espace-temps dans lequel nous vivons a 4 dimensions (d'où la difficulté à le dessiner): trois d'espace, et une de temps. (Enfin, certains, dont justement Brian Greene, pensent qu'il y a en fait 10 dimensions, voire 26, mais laissons ça de côté pour le moment (apparemment, on a plus de côtés où laisser ça que prévu)).
En fait, même si la relativité d'Einstein a consacré l'usage de ces diagrammes d'espace-temps, le point qui nous intéresse ici, à savoir la nature du temps en physique, était déjà d'actualité lorsque Newton a mis au point la mécanique classique: le temps, c'est une dimension, un axe supplémentaire dans la description du monde.

By Hermann Minkowski, died 1909 - Space and Time: Minkowski's Papers on Relativity, published by the Minkowski Institute. The image had appeared on the cover of The Mathematical Intelligencer, Volume 31, Number 2 (2009)., Public Domain, Link
Dans ce modèle, l'univers est donc un bloc, contenant tous les endroits et tous les instants dans un seul objet. Le "présent" n'est qu'une tranche (d'épaisseur nulle) parmi d'autres de ce bloc, et n'a aucun statut particulier. Le futur "existe" déjà: il est entièrement déterminé, via les équations de la mécanique, à partir des conditions initiales de l'univers. Autrement dit, si on connaît parfaitement la position et la vitesse des particules à l'instant initial $t=0$, on peut calculer leur position à n'importe quel instant futur. C'est ce que l'on appelle le déterminisme.
Depuis sa première vérification expérimentale en 1919, la théorie de la relativité générale d'Einstein n'a fait qu'accumuler les succès. L'univers-bloc contenant passé, présent et futur est donc, naturellement, le cadre de travail de la majorité des chercheurs en physique.
Pourtant, si la relativité générale est en mesure de prédire les phénomènes les plus étranges au voisinage des trous noirs avec une précision saisissante, il est un phénomène qu'elle n'explique pas: le passage du temps. Comment passe-t-on d'une tranche à la "suivante" ? Einstein lui-même, en 1955 a (peut-être) dit "Pour les physiciens, la distinction entre le passé, le présent et l'avenir n'est qu'une illusion, même si elle est têtue. "
Et cette illusion est, de fait, très têtue. Et tenter de déterminer qui, des équations de la relativité ou de 8 milliards de tas de gelée grise contenus dans nos crânes, détient la meilleure représentation de la vraie réalité, est une question qui nous emmène vers les sommets de la philosophie (les livres d'Etienne Klein sont une excellente façon de ressentir quelques vertiges à ce sujet).
Physique quantique: la némésis de la relativité générale
La relativité générale d'Einstein est l'une des deux théories qui ont révolutionné la phhysique du XXème siècle. L'autre, c'est la physique quantique (celle qui implique un chat mort-vivant dans une boîte). Ses succès expérimentaux sont tout aussi innombrables que ceux de la relativité générale, malgré des prédictions pour le moins contre-intuitives. C'est une histoire passionnante, mais qui nous emmènerait bien trop loin. L'excellente chaîne Looking Glass Universe le fait déjà très bien:
Le point qui nous intéresse particulièrement ici est le rôle du passage du temps en physique quantique. En effet, dans ce cadre, une particule donnée existe dans une superposition de tous ses états possibles, jusqu'à ce qu'on la mesure: à ce moment, elle adopte un de ces états, et c'est ce que l'on mesure. Chaque état a une certaine probabilité d'être mesuré, et au moment de la mesure, la particule "choisit" un de ces états au hasard, en suivant cette loi de probablité.
Ainsi, supposons que l'une des propriétés de la particule est sa couleur, mettons soit bleue soit rouge, et que les deux couleurs ont la même probabilité 1/2. Alors, dans le cadre de la physique quantique (plus précisément, dans son interprétation la plus commune), tant qu'on ne la regarde pas, la particule est à la fois bleue et rouge. Plus précisément, elle est dans un "état superposé", que l'on note $\frac12|bleue\rangle + \frac12|rouge\rangle$. Une fois qu'on la regarde (autrement dit, au moment où on la "mesure"), il faut bien que la particule ait une couleur et une seule; elle passe alors dans l'état $|bleue\rangle$ avec une probabilité $\frac 12$, ou dans l'état $|rouge\rangle$ avec une probabilité $\frac 12$.
Cet état superposé est extrêmement bizarre: il semblerait beaucoup plus raisonnable de supposer que, si on a mesuré que la particule était bleue, alors elle était déjà bleue avant, et qu'il se trouve simplement que la moitié des particules sont bleues et l'autre moitié rouge. Or, ce n'est en fait pas le cas, et on peut le démontrer expérimentalement:
(Pour encore plus de bizarreries, voir ici et là).
Ne perdons pas le fil: on voulait parler de temps. Dans l'univers-bloc qui sert de cadre à la relativité, tous les instants ont le même statut, et tous les changements sont réversibles. Mais en physique quantique, ce n'est pas le cas: au moment de la mesure, quelque chose d'irréversible se produit, quand la particule passe d'un état superposé à un état "défini" (ou "pur"). Et cet évènement est fondamentalement aléatoire: rien ne permet de prédire le résultat avant d'avoir effectué la mesure. Autrement dit, la mécanique quantique est une description indéterministe de l'univers.
C'est l'une des nombreuses divergences d'opinions entre la mécanique quantique et la théorie de la relativité.
Construire le temps: la proposition de Nicolas Gisin
C'est là que Nicolas Gisin entre en scène, et la solution qu'il propose est de nature mathématique, et non physique. Pour lui, tous nos malheurs viennent des outils mathématiques classiques qu'on utilise pour modéliser la réalité, et les principaux coupables sont les nombres, eh bien, réels.
Reprenons notre univers-bloc. Il contient le futur, car c'est un univers déterministe: si on connaît parfaitement les conditions initiales, on peut en déduire l'état futur du système à tout instant ultérieur. La seule raison pour laquelle on n'y arrive pas (par exemple, la raison pour laquelle on a tant de mal à prévoir la météo), c'est tout simplement parce qu'on ne peut pas connaître les conditions initiales avec une précision infinie: nos outils de mesure ne nous le permettent pas. Et quand bien même, elles représentent une quantité monstrueuse d'information, qu'on serait bien en peine de traiter !
Mais elles existent bel et bien, ces conditions initiales: on a juste de trop gros doigts pour les attraper.
C'est là que Nicolas Gisin n'est pas d'accord. Ces conditions initiales représentent de l'information; or, selon la recherche récente, l'information n'est pas une substance éthérée qui vit dans un espace abstrait: c'est une quantité physique, qui prend de la place. En fait, on peut montrer qu'il existe une densité maximale d'énergie dans un volume d'espace donné: c'est la limite de Bekenstein.
Pour donner un sens physique à l'information, on considère que si un système $S$ a $N$ états possibles, alors son information est $I(S)=\log(N)$ (si on prend un logarithme de base 2, l'information est alors comptée en bits). L'avantage de cette façon de faire, c'est qu'alors, deux systèmes indépendants $S_1$ et $S_2$, ayant respectivement $N_1$ et $N_2$ états possibles, ont conjointement $N_1N_2$ états possibles; donc l'information que le système total $S$ contient est $$I(S)=\log(N_1N_2)=\log(N_1)+\log(N_2)=I(S_1)+I(S_2),$$ ce qui correspond à l'intuition.
La limite de Bekenstein majore l'information contenue dans une région d'espace de volume et de masse finis. Plus précisément, considérons un système $S$ de masse $M$ contenu dans une sphère de rayon $R$, alors $$I(S)\leq \dfrac{2\pi RMc}{\hbar \ln(2)}\simeq 2,6.10^{43} RM,$$ où $\hbar$ est la constante de Planck et $c$ la vitesse de la lumière. Autrement dit, la densité maximale d'information est de l'ordre de $10^{43}$ bits par kilo et par mètre cube: c'est beaucoup, certes (plus que ma clé USB, en tout cas. Remboursez), mais ce n'est pas une infinité.
Cette limite a été obtenue en étudiant l'application de la thermodynamique aux trous noirs: c'est une histoire passionnante (dont le protagoniste, Stephen Hawking, vous est peut-être familier), qui sera contée une autre fois. Il faut tout de même noter que, si l'existence d'une limite fait à peu près consensus, la formulation exacte est encore débattue.
Mais les conditions initiales de l'univers sont des réels, qui représentent l'état de chaque particule avec une précision infinie: c'est, selon Gisin, beaucoup trop d'information à faire rentrer dans trop peu d'espace. Pour contourner ce problème, il faudrait abandonner les nombres réels "classiques", et se tourner vers les mathématiques constructives de Brouwer.
Comme on l'avait vu ici, en analyse constructive, un réel $x$ est représenté par une suite de rationnels $(x_n)_n$ telle que $ |x_n - x_p| < \frac 1n + \frac 1p.$ Deux suites régulières $(x_n)$ et $(y_n)$ définissent le même réel si, pour tout $n$, $ |x_n - y_n| < \frac 2n$.
Par exemple, on peut imaginer représenter un réel en ajoutant des décimales. Ainsi, $\pi$ peut être représenté par la suite $x_1=3,x_2=3.1, x_3=3.14....$ mais aussi par la suite $y_1=3.1, y_2=3.11, y_3=3.141....$.
Attention, j'ai triché: les "..." ne sont pas autorisés en mathématiques constructives. Comme le nom l'indique, pour utiliser un objet en mathématiques constructives, il faut disposer d'un procédé qui construit cet objet. Pour une suite, il s'agit, soit d'une "loi" qui décrit qui est le premier terme et comment on passe d'un terme au suivant, par exemple "ajouter 1", mais aussi, éventuellement, "jeter un dé et ajouter le résultat comme décimale".
De cette manière, les nombres eux-mêmes dépendent du passage du temps, et se construisent au fur et à mesure. Et cela empêche de connaître toutes leurs propriétés. Par exemple, prenons un réel $x=0.4999????$ où les ? sont remplacés progressivement par des décimales suivant un certain procédé. On veut savoir si $x<\frac12$. Eh bien.... on ne peut pas encore. Si la suite de $9$ se poursuit indéfiniment, alors $x=\frac12$. Mais si, à un moment, apparaît une décimale plus petite que 9 (par exemple $x=0.499999999999997???$), alors on sera certains que $x<\frac12$. En attendant, la proposition $"x<\frac 12"$ n'est ni vraie ni fausse.
Ainsi, on ne peut pas non plus séparer proprement nos réels entre ceux qui sont plus petits que $\frac12$ et ceux qui sont plus grands. A chaque instant, il reste des réels différents de $\frac12$ dont on ne sait pas encore qu'ils sont différents: ils "collent au couteau" quand on essaie de couper notre miche de pain cosmique en $t=\frac12$.
En utilisant ce type de mathématiques, Gisin et son collaborateur Flavio Del Santo ont obtenu une version constructive de la mécanique classique, qui devient donc fondamentalement indéterministe. Cela ne signifie pas qu'on ne peut faire aucune prédiction: on peut rapprocher cette construction des systèmes chaotiques (cette théorie avec une histoire de papillon au Brésil qui provoque des tempêtes pendant mon weekend. Que quelqu'un l'écrase.) pour lesquels on peut faire des prédictions à court terme, mais pas à long terme car ils dépendent de la précision de mesure des conditions initiales.
Il s'agit là de toutes nouvelles idées, qui n'ont pas encore été entièrement développées. Gisin projette maintenant de s'atteler à la reformulation de la relativité et de la mécanique quantique en mathématiques "floues". Ces travaux, qui font miroiter un rapprochement entre les deux théories ennemies, suscitent déjà un vif intérêt. Et, sur ce cliffhanger, il ne nous reste plus qu'à attendre la saison 2.