Matrices

Motivation.

Les matrices sont des tableaux de nombres, munis de règles de calcul qui facilitent la résolution opératoire d'un certain nombre de problèmes:

• Les systèmes linéaires, dont on a déjà pas mal parlé au chapitre précédent:

  On a mentionné, par exemple, que le système

  \begin{equation*} \begin{cases} \begin{array}{rcrcrc} x \amp +\amp 2y \amp =\amp m \cr \amp \amp 3y \amp =\amp p\cr \end{array} \end{cases} \end{equation*}

  peut se représenter "matriciellement" comme ceci:

  \begin{equation*} \begin{pmatrix} 1 \amp 2\\0 \amp 3 \end{pmatrix}\cdot \begin{pmatrix} x\\y \end{pmatrix}= \begin{pmatrix} m\\p \end{pmatrix} \end{equation*}

  et "résoudre le système" revient à trouver des coefficients réels \(\alpha,\beta,\gamma,\delta\) tels quequi permettent d'écrire \(x\)et \(y\) en fonction de \(m\) et \(p\text{:}\)

  \begin{equation*} \begin{cases} \begin{array}{crcrcr} x \amp =\amp \alpha m \amp + \amp \beta p \cr y \amp =\amp \gamma m \amp + \amp \delta p\cr \end{array} \end{cases} \end{equation*}

  ou encore, "matriciellement",

  \begin{equation*} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} \alpha\amp \beta\\\gamma\amp \delta \end{pmatrix} \cdot \begin{pmatrix} m\\p \end{pmatrix} \end{equation*}

  Le but de ce chapitre, entre autres,, va être d'expliquer à quoi correspond cette opération \(\cdot\) et la matrice \(\begin{pmatrix} \alpha\amp \beta\\\gamma\amp \delta \end{pmatrix}\text{.}\)

• Bases d'espaces vectoriels ¹

• Représentation des applications linéaires: on verra que les matrices représentent aussi des transformations du plan, de l'espace ².

  Par exemple, notre matrice \(\begin{pmatrix} 1 \amp 2\\0 \amp 3 \end{pmatrix}\) peut être vue comme une opération qui transforme \((x,y)\in\R^2\) en \((m,p)\in\R^2\text{,}\) ce qui ressemble à ça:

  

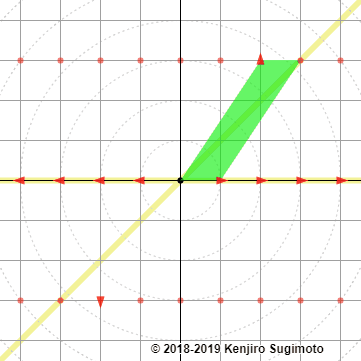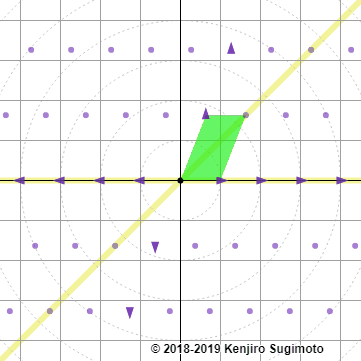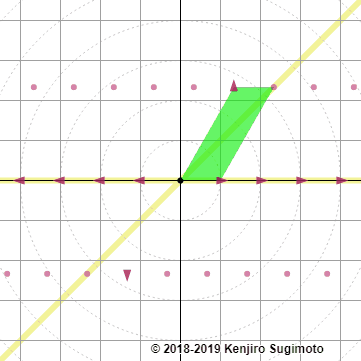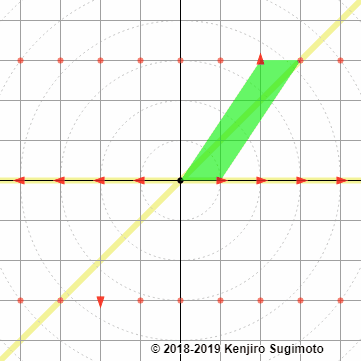
Introduisons donc sans plus attendre les règles de calcul qui nous permettront de rendre tout ça sensé.

Notation: Dans ce chapitre, on note \(\K=\R\) ou \(\C\text{,}\) et on l'appelle l'ensemble des scalaires.