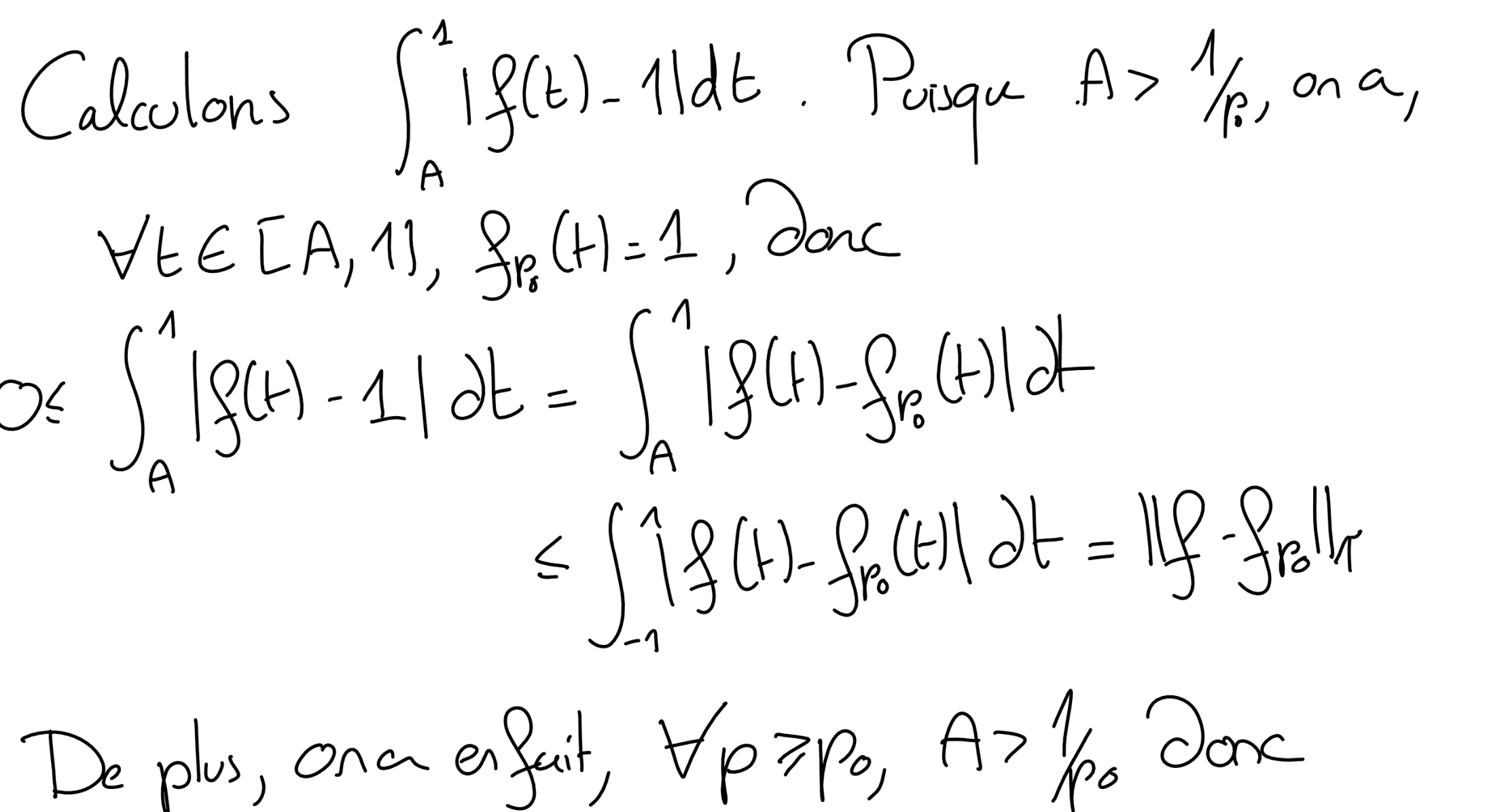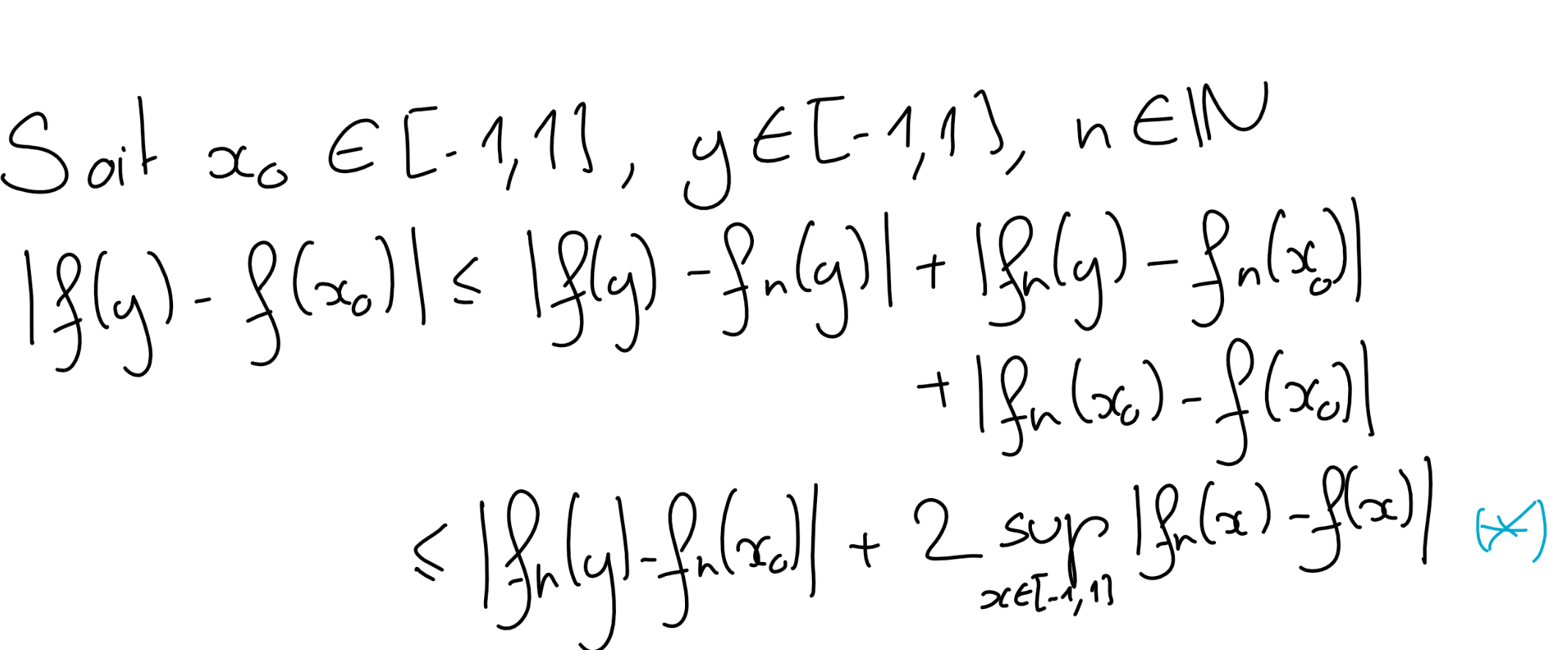\(C^0([-1,1],\mathbb R)\) est complet pour \(\|.\|_\infty\) mais pas pour \(\|.\|

Section 2 \(C^0([-1,1],\mathbb R)\) est complet pour \(\|.\|_\infty\) mais pas pour \(\|.\|_1\text{.}\)

Notons \(E=C^0([-1,1],\mathbb R)\) l'espace vectoriel des fonctions réelles continues sur \([-1,1]\text{.}\) On le munit des deux normes suivantes: pour \(f\in E\text{,}\)

\begin{gather*} \|f\|_\infty = \max_{x\in[-1,1]}|f(x)|\\ \|f\|_1=\int_{-1}^1 |f(t)|dt \end{gather*}

Project 2.1. Comparaison des normes.

(a)

Ces deux normes sont-elles équivalentes ?

Hint

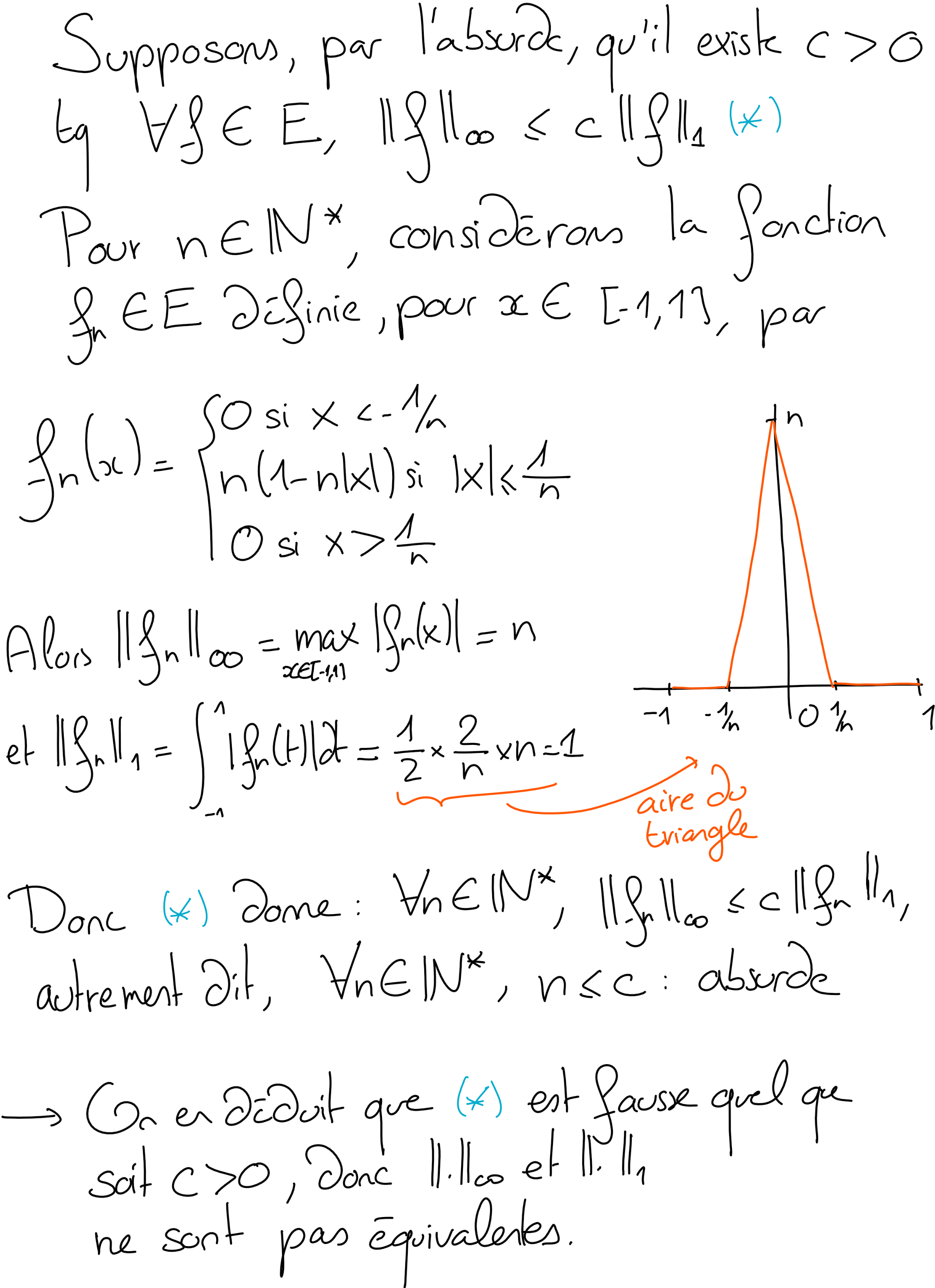
Supposer par l'absurde qu'il existe \(c\gt 0\) tel que pour toute \(f\in E\text{,}\) \(\|f\|_\infty \leq c\|f\|_1\text{,}\) puis trouver une suite \((f_n)_n\in E^{\mathbb N}\) telle que

\begin{equation*} \begin{cases} \|f_n\|_\infty \xrightarrow[n\rightarrow \infty]{} +\infty\\ \|f_n\|_1=1 \end{cases} \end{equation*}

pour obtenir une contradiction.

Indice: Les \((f_n)\) sont des fonctions "pointues".

Solution

(b)

Montrer que si une suite \((f_n)_n \in E^{\mathbb N} \) converge dans \((E,\|.\|_\infty)\) alors elle converge vers la même limite dans \((E,\|.\|_1)\text{,}\) mais que la réciproque est fausse.

Hint

Utiliser la question précédente et l'exercice 3 du TD6

Solution

Project 2.2. \((E,\|.\|_1)\) n'est pas complet.

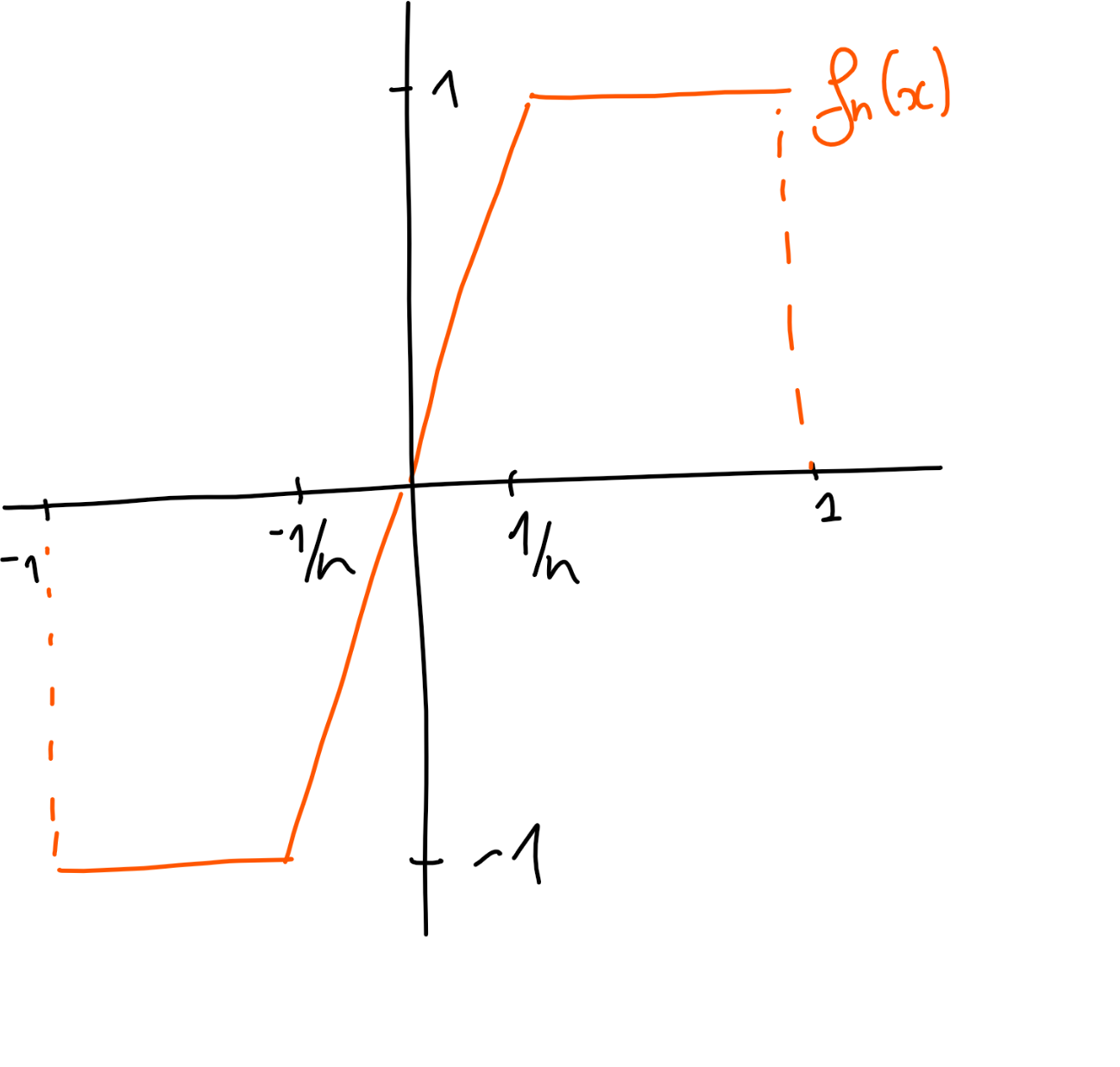
On considère la suite de fonctions \((f_n)_n \in E^{\mathbb N} \) définie par

\begin{equation*} f_n: x \in [-1,1]\mapsto \begin{cases} -1 \amp\text{ si } x \lt -1/n\\ nx \amp\text{ si } -1/n \lt x \lt 1/n\\ 1 \amp\text{ si } x \gt 1/n\\ \end{cases} \end{equation*}

(a)

Dessiner une allure des fonctions \(f_n\text{.}\)

Solution

(b)

Montrer que \((f_n)_n\) est de Cauchy dans \((E,\|.\|_1)\text{.}\)

Hint

Pour \(p,q\in \mathbb N\text{,}\) on commence par calculer

\begin{equation*} f_{p+q}(t)-f_p(t) = \begin{cases} 0 \amp\text{ si } x \lt -1/p\\ -1-px \amp\text{ si } -1/p \lt x \lt -1/(p+q)\\ qx \amp\text{ si } -1/(p+q) \lt x \lt 1/(p+q)\\ 1-px \amp\text{ si } 1/(p+q) \lt x \lt 1/p\\ 0 \amp\text{ si } x \gt 1/p\\ \end{cases} \end{equation*}

Graphiquement, on a:

Solution

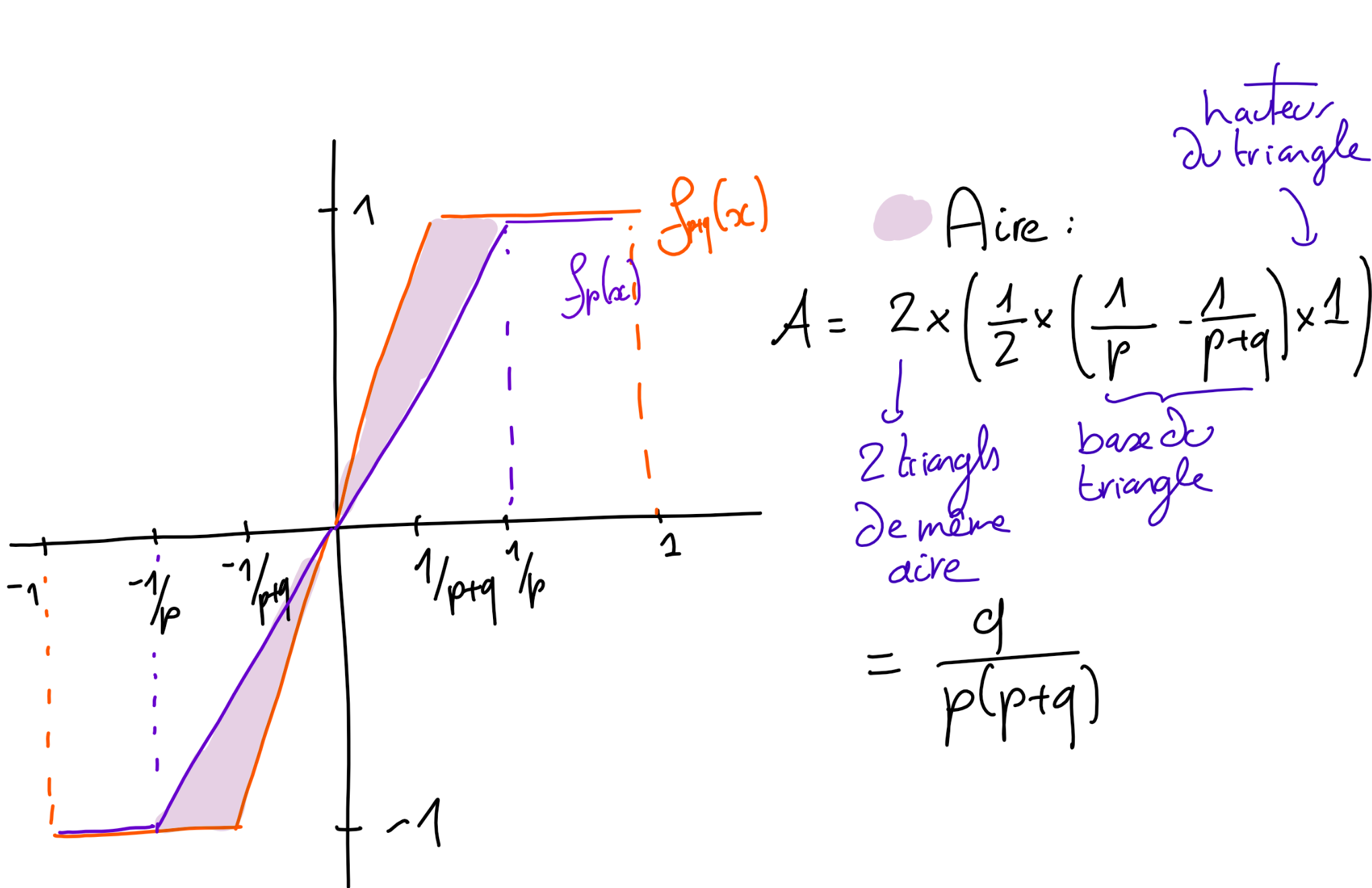
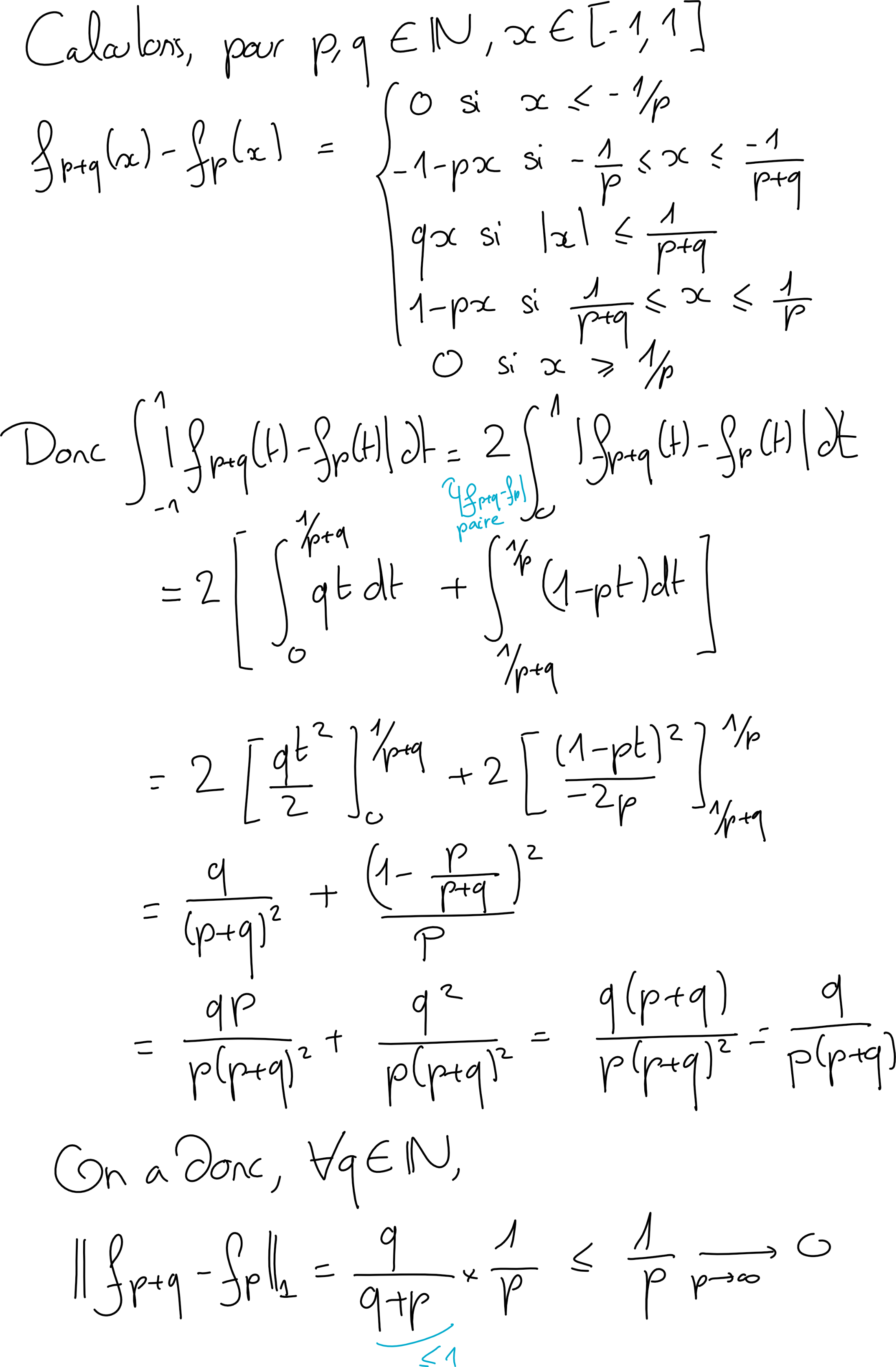
(c)

Supposons, par l'absurde, que \((f_n)_n\) converge dans \((E,\|.\|_1)\) vers une fonction \(f\in E\text{.}\) Soit \(A\gt 0\) et \(p_0\in \mathbb N^*\) tel que \(\frac 1{p_0} \lt A\text{.}\) Montrer que

\begin{equation*} \int_A^1 |f(t)-1|dt =0 \end{equation*}

et, de là, que \(f\) n'est pas continue en 0, ce qui contredit \(f\in E\text{.}\)

Hint

Pour la dernière partie, utiliser la négation de la continuité en 0 avec \(\varepsilon = 1\text{:}\) montrer que pour tout \(\delta \gt 0\text{,}\) il existe \(x\in [-1,1]\) tel que \(|x-0|\lt \delta\) mais \(|f(x)-f(0)|\geq 1\text{.}\)

Solution

(d)

Conclure que \((E,\|.\|_1)\) n'est pas complet.

Solution

Project 2.3. \((E,\|.\|_\infty)\) est complet.

Soit \((f_n)_n \in E^{\mathbb N} \) une suite de Cauchy dans \((E,\|.\|_\infty)\)

(a)

Soit \(x\in [-1,1]\text{.}\) Montrer que la suite \((f_n(x))_n \in \mathbb R^{\mathbb N}\) est de Cauchy dans \(\mathbb R\text{.}\) En déduire qu'elle converge vers un réel \(f(x)\text{.}\) Ceci définit une fonction \(f:[-1,1]\rightarrow \mathbb R\text{.}\)

Solution

(b)

Montrer que, pour tout \(x\in [-1,1]\text{,}\)

\begin{equation*} |f_{p+q}(x)-f_p(x)|\leq \sup_{s\in \mathbb N}\|f_{p+s}-f_p\|_\infty \end{equation*}

et en déduire que \(\sup_{x\in [-1,1]}|f_n(x) - f(x)|\rightarrow 0\text{.}\)

Solution

(c)

Soit \(x_0\in [-1,1]\text{.}\) Montrer que pour tout \(y\in [-1,1]\) et pour tout \(n\in \mathbb N\text{,}\) on a:

\begin{equation*} |f(y)-f(x_0)|\leq |f_n(y)-f_n(x_0)|+2\sup_{x\in [-1,1]}|f_n(x) - f(x)| \end{equation*}

En déduire que \(f\in E\text{.}\)

Solution

(d)

Conclure que \((E,\|.\|_\infty)\) est complet.

Solution