Des ensembles aux ensembles de nombres

Comme on en a discuté ici, la théorie axiomatique des ensembles de Zermelo et Fraenkel est la façon la plus couramment utilisée de "fonder" les mathématiques, c'est-à-dire de baser toutes les preuves et tous les objets mathématiques sur une poignées d'affirmations (les axiomes) portant sur des ensembles.

Cependant, telle que présentée dans mon précédent post, la théorie ZFC peut sembler quelque peu...aride: il n'y vit que des ensembles, justement, et encore, seul l'ensemble vide et un étrange ensemble infini ont réellement été observés.

Il semble qu'il y ait un peu de terraformation à faire avant de pouvoir faire des maths confortablement. Déjà, si on avait les nombres, allez, les nombres entiers, on se sentirait un peu plus en terrain connu. Peut-être aussi des fonctions pour agir dessus, si possible ?

Cette page a pour but de rendre la théorie ZFC un peu plus viable pour les êtres humains.

Paires ordonnées

Commençons pas quelque chose de si modeste qu'il est facile d'oublier qu'on ne l'a pas encore: les paires ordonnées, ou couples $(a,b)$. SI $a$ et $b$ sont deux ensembles, on a vu que l'axiome de la paire nous permet de former l'ensemble $\{a,b\}$, mais celui ci est égal à $\{b,a\}$ et si $a$ et $b$ sont égaux, au singleton $\{a\}$.

D'un autre côté, comment donner un statut à l'ordre dans lequel arrivent les éléments de la paire ? On a envie de dire que "a arrive avant b" dans $(a,b)$, ce que l'on pourrait noter $a \preccurlyeq b$. Quel sens donner à ce $\preccurlyeq$ avec ce qu'on a déjà ?

Lao-Tzeu (et Baloo) a dit

Celui qui sait se satisfaire aura toujours le nécessaire.

Le seul semblant d'ordre que l'on ait, c'est l'inclusion. On pourrait donc isoler le premier élément du couple dans un singleton $\{a\}$, et l'inclure dans quelque chose...par exemple, dans $\{a,b\}$. Un candidat pour notre paire ordonnée est donc:

$$(a,b):= \{\{a\}, \{a,b\}\}$$

Comment vérifier que cette écriture, bien peu naturelle, a bien les propriétés qu'on attribue habituellement à une paire ordonnée ? On voit assez vite qu'avec cette définition, $(a,b)=(b,a)$ si et seulement si $a=b$. En effet, si $a=b$, alors $(a,b) = \{\{a\}, \{a,b\}\} = \{\{a\}, \{a\}\} = \{\{a\}\} = (b,a)$. Réciproquement, si $a\neq b$, alors $\{a\} \neq \{b\}$ et $\{a\}\neq \{a,b\}$, donc $\{a\} \in (a,b)$ mais $\{a\} \notin (b,a)$, donc $(a,b) \neq (b,a)$. Mais est-ce que cela suffit ?

La propriété qui caractérise complètement les paires ordonnées s'écrit en fait

$$(a,b) = (x,y) \text{ ssi } a=x \text{ et } b=y \tag{1}$$

Et notre définition fait bien le travail: si $(a,b)=(x,y)$, alors

• soit $a=b$, donc $(a,b)$ est un singleton, donc $(x,y)$ aussi, et on déduit que $x=y=a$;
• soit $a\neq b$, et en séparant les deux cas possibles $\{a\} = \{x\}$ ou $\{a\}= \{x,y\}$, on voit assez vite que la seule option viable est $\{a\} = \{x\}$ et $\{a,b\} = \{x,y\}$, d'où $a=x$ et $b=y$.

ZFC nous permet donc de récupérer, quoique sous une forme assez laide, les paires ordonnées: à partir de maintenant, on les notera de la façon usuelle $(a,b)$ et on peut oublier leur sombre origine.

La prochaine étape consiste à se demander si on est autorisé à parler de l'ensemble de toutes les paires ordonnées. Cela peu sembler immédiat, mais ce genre de raccourci a causé la perte de la théorie naïve des ensembles ! ZFC permet de créer facilement des sous-ensembles, mais se méfie des ensembles trop gros. On va donc commencer par trouver un gros ensemble licite dans lequel vivent tous les $(a,b)$ pour $a\in A$ et $b\in B$, puis le restreindre.

D'après l'axiome de l'union, $\{a,b\}\subset A\cup B$, et $\{a\}\subset A\cup B$, donc (axiome de l'ensemble des parties) $\{a\}$ et $\{a,b\}$ sont des éléments de $\mathcal P(A\cup B)$, donc $(a,b)= \{\{a\}, \{a,b\}\}$ est un sous-ensemble de $\mathcal P(A\cup B)$, donc un élément de $\mathcal P(\mathcal P(A\cup B))$. On peut maintenant utiliser l'axiome de compréhension pour définir le produit cartésien:

$$A \times B := \{x \in \mathcal P(\mathcal P(A\cup B)),\, \exists a \in A,\, \exists b \in B,\,x=(a,b)\}$$

A partir de là, obtenir des triplets ordonnés, puis des quadruplets ordonnés ne coûte pas cher: on itère le procédé qui a si bien marché pour les paires. Ainsi,

$$(a,b,c):=\{\{(a,b)\}, \{(a,b),c\}\} $$ $$(a_1,\dots,a_n):= \{\{(a_1,\dots,a_{n-1})\}, \{(a_1,\dots,a_{n-1}),a_n\}\} $$

Remarquons que ce n'est pas la seule façon de faire: on peut aussi décider que $(a,b,c)= \{\{a\},\{a,b\},\{a,b,c\}\}$, et cette définition fait aussi le café. Ce n'est pas alarmant: toute l'idée de la méthode axiomatique est de trouver les propriétés qui nous intéressent, et disposer d'objets qui les vérifient; pour les $n$-uplets, du moment qu'ils vérifient (1), on pourra les utiliser, où que soient les accolades, parenthèses, et autres symboles cabalistiques permettant de les invoquer.

Relations

On va maintenant s'essayer à donner un sens à la notion de relation en mathématiques. Des relations, il y en a partout, de toutes les formes, couleurs et convictions:

• Sur n'importe quel ensemble $A$, la relation d'égalité $x=y$ pour $x,y\in A$
• La relation d'ordre $x< y$ est une relation binaire sur $\mathbb R$
• La relation "$M, P,Q$ sont alignés" est une relation ternaire sur les points du plan
• La relation "$M$ est le milieu de $[P,Q]$" est soit une relation ternaire sur les points du plan, soit une relation binaire sur les points du plan d'une part, et les segments d'autre part
• La relation "sont les parents de" est une relation binaire sur les couples de personnes d'une part et sur les personnes individuelles d'autre part: "(Lily, James) sont les parents de Harry"

Si disparates qu'elles soient, toutes ces relations ont une chose en commun: elles n'ont pas une tête d'ensemble ! Et pourtant, il va bien falloir. Quel ensemble pourrait exprimer une relation ?

C'est ici que le produit cartésien revient à la charge: une relation binaire $R$ sur deux ensembles $A$ et $B$ sera un sous-ensemble du produit cartésien $A\times B$. On dira alors, pour $a \in A$ et $b\in B$, que $a$ est en relation $\mathcal R$ avec $b$ (noté $a \mathcal Rb$) si $(a,b)\in R$.

Par exemple, la relation d'égalité sur $A$ est définie par $\{(x,y) \in A \times A, x=y\}$. Un autre exemple est la relation d'appartenance à un sous-ensemble, définie par $\{(x,B) \in A \times \mathcal P(A), x\in B\}$.

Munis de cette définition, on peut attribuer aux relations toutes sortes de qualificatifs: réflexive, symétrique, anti-symétrique, transitive... On reviendra sur quelques-uns de ces termes.

Et, plus généralement, une relation $n$-aire sur $A_1,\dots,A_n$ correspondra à un sous-ensemble du produit cartésien $A_1\times\dots\times A_n$.

Relations d'équivalence

Une certain type de relation, les relations d'équivalences servent à "imiter" l'égalité, en en extrayant les propriétés essentielles. Que doit vérifier une relation $\mathcal R$ pour être "une sorte d'égalité" ? Tout d'abord, $R$ doit être une relation binaire sur $A\times A$ pour un certain ensemble $A$. De plus,

• on veut que $x$ soit en relation avec lui-même: $x\mathcal R x$ (réflexivité)
• On veut que, si $x\mathcal R y$, alors $y \mathcal R x$ (symétrie)
• enfin, on veut que, si $x\mathcal R y$ et $y\mathcal R z$, alors $x\mathcal R z$ (transitivité)

L'égalité sur $A$ vérifie ces axiomes. Si $A$ est l'ensemble des évènements, alors "se produire à la même date" (par exemple le 3 décembre) est une relation d'équivalence qui n'est pas l'égalité.

La relation d'ordre $x\leq y$ sur $\mathbb R$ n'est pas une relation d'équivalence: elle est réflexive et transitive, mais pas symétrique. La relation sur les points du plan, "$P \mathcal R Q$ si $Q$ est dans le disque de centre $P$ et de rayon 2" n'en est pas une non plus: elle est réflexive et symétrique, mais pas transitive. Idem pour la relation sur les réels donnée par $x\mathcal R y$ si l'écriture décimale de $x$ et $y$ diffère d'au plus un chiffre. (Devinette: y a-t-il des relations symétriques, transitives, mais pas réflexives ?)

Au vu de ces exemples et contre exemples, cette définition semble bien capturer la notion d'équivalence. Mais pour quoi faire ?

Un des intérêts des relations d'équivalence est de permettre de parler de catégories d'objets; par exemple, la relation d'équivalence "appartenir à la même espèce" sur l'ensemble des animaux permet de parler des girafes en général plutôt que de devoir donner des noms à chaque individu. De ce point de vue, on voit aussi que les relations d'équivalences sont liées à la notion de partition: une partition d'un ensemble $X$, c'est une collection de sous-ensembles de $X$, non vides, disjoints, et dont l'union est égale à $X$. Dans l'exemple ci-dessous, $X$ est l'ensemble des livres (les objets avec des pages), et la relation d'équivalence est "avoir le même ISBN". On obtient ainsi des catégories qui contiennent tous les exemplaires de la même édition d'un livre donné.

Par Nuvola apps bookcase.svg: Peter Kemp derivative work: Stephan Kulla (User:Stephan Kulla) — Nuvola apps bookcase.svg, LGPL, Lien

Par Nuvola apps bookcase.svg: Peter Kemp derivative work: Stephan Kulla (User:Stephan Kulla) — Nuvola apps bookcase.svg, LGPL, Lien

Si $\mathcal R$ est une relation d'équivalence sur $A$, alors les ensembles de la forme

$$[x]:=\{y\in A, x\mathcal R y\}$$

forment une partition de $A$ (on appelle $[x]$ la classe d'équivalence de $x$). Inversement, si les $(A_i)$, où $A_i \in \mathcal P(A) \setminus \{\emptyset\}$, forment une partition de $A$, alors ils définissent la relation d'équivalence "$x\mathcal R y$ ssi il existe $i$ tel que $x,y \in A_i$.

L'ensemble des classes d'équivalences pour une relation d'équivalence $\mathcal R$, $\{[x], x \in A\}$ est un sous-ensemble de $\mathcal P(A)$, on peut donc légalement lui donner un permis de séjour dans ZFC. On l'appelle l'ensemble quotient de $A$ par $\mathcal R$, noté $X/\mathcal R$. Ce type d'ensemble est omniprésent en mathématiques: dès que l'on veut mettre des choses différentes dans la même boîte, on fait un quotient. C'est aussi ce que font les pendules: tous les moments espacés de 12h correspondent au même point sur le cadran.

Fonctions

Tout comme que les relations, les fonctions sont omniprésentes en mathématiques, encore plus diverses que les espèces sous-marines, et, tout comme les relations, elles n'ont pas du tout une tête d'ensemble. On voit habituellement les fonctions comme des machines à transformer un objet, disons $x$, en un nouvel objet $f(x)$:

By Wvbailey (talk) - Own work, Public Domain, Link

Comme toujours, la clé va être d'utiliser ce qu'on a construit avant: on va envisager les fonctions comme un type particulier de relation. Plus précisément, on va vouloir mettre en relation chaque $x$ de l'ensemble de départ avec son image $f(x)$ dans l'ensemble d'arrivée. La question est donc: à quelles conditions une relation binaire, c'est à dire un sous ensemble de $X\times Y$, correspond-elle à l'idée qu'on se fait d'une fonction $f: X \rightarrow Y$?

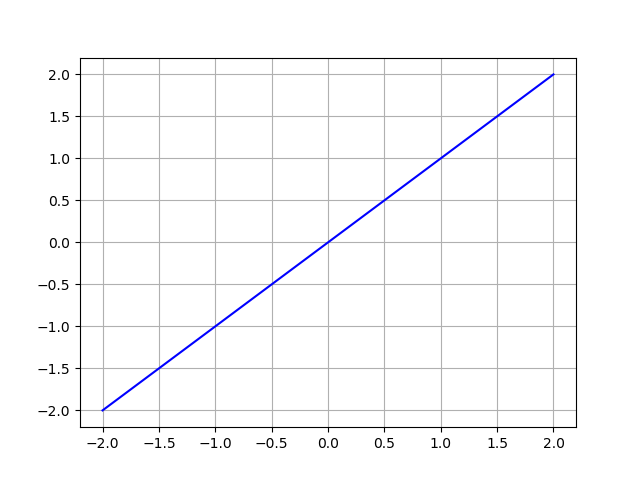
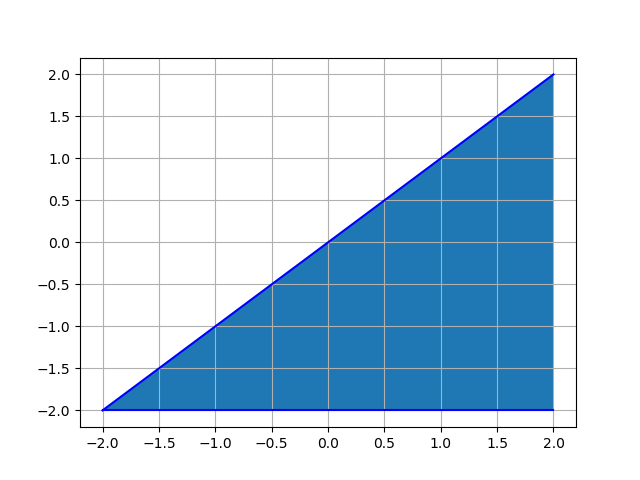
Parmi les exemple qu'on a déjà croisé, la relation d'égalité sur $\mathbb R$ (par exemple) peut être vue comme la fonction $ \mathbb R \rightarrow \mathbb R, x \mapsto x$. Par contre, la relation d'ordre $x\leq y$ sur $\mathbb R$ ne correspond pas à une fonction $f: \mathbb R \rightarrow \mathbb R$. Vues comme sous ensemble de $\mathbb R^2$, ces relations correspondent à:

Relation d'égalité

Relation d'ordre

Ce qui semble différencier ces deux cas, c'est que dans le premier, pour chaque $x \in \mathbb R$, on a un seul $y$ (en l'occurrence, égal à $x$) qui lui correspond; tandis que dans le deuxième, à chaque $x$, une infinité de $y$ sont en relation avec $x$. C'est précisément cette notion d'unité qui caractérise les fonctions, et qui, dans le cas de fonctions sur $\mathbb R$, donne à la région correspondante de $\mathbb R \times \mathbb R$ l'aspect d'une ligne, plutôt que d'une surface.

Formalisons cette idée: une fonction $f:A\rightarrow B$ sera donc une relation binaire $f\subset A\times B$, telle que si $(x,y)$ et $(x,z)$ sont deux éléments de $f$, alors $y=z$. Autrement dit, un même "antécédent" $x$ ne peut avoir deux "images" différentes $y$ et $z$. Comme l'image d'un $x$ est unique, cela fait sens de lui donner un nom, qui fait intervenir $x$, par exemple, au hasard, $f(x)$.

Les fonctions de $A$ dans $B$ étant des cas particuliers de sous-ensembles de $A\times B$, autrement dit des éléments de $\mathcal P(A\times B)$, l'ensemble de toutes les fonctions est bien légal dans ZFC, comme sous ensemble de $\mathcal P(A\times B)$. On le note $B^A$.

Quelques exemples: On a déjà parlé de la fonction correspondant à la relation d'égalité sur $A$; on l'appelle identité. Un autre cas, lié au précédent, est celui où $A \subset B$ et $f=\{(x,y)\in A \times B, x=y\}$: $f$ est alors la fonction d'inclusion de $A$ dans $B$. Dans le cas où $A$ est un produit cartésien $X\times Y$, on peut définir les projections $f_X$ sur $X$ et $f_Y$ sur $Y$:

$$f_X= \{(a=(x,y),z)\in A\times X, x=z\}$$ $$f_Y= \{(a=(x,y),t)\in A\times Y, y=t\}$$

Un autre exemple provient de la construction des ensembles quotients dans la section précédente: si $\mathcal R$ est une relation d'équivalence sur $A$, on peut définir la fonction de $A$ dans $A/\mathcal R$ qui à chaque élément associe sa classe d'équivalence:

$$f = \{(x,E) \in A \times \mathcal P(A), E=[x]\}$$

Anticipons un peu et supposons qu'on a déjà construit les nombres, ou au moins qu'on a déjà construit 0, 1 et donné un sens à l'ensemble $\{0,1\}$ (présomptueux, je sais). Soit maintenant $E$ un sous-ensemble de $A$; on peut définir la fonction $f_E$ de $A$ dans $\{0,1\}$, définie par:

$$x\in A \mapsto \begin{cases} 1 \text{ si } x \in E,\\ 0 \text{ si } x \notin E \end{cases} $$

(Devinette: comment l'écrire sous forme d'un ensemble ? Ou peut-être de l'union de deux ensembles ?). On l'appelle la fonction indicatrice de $E$. Remarquons que, réciproquement, à chaque fonction $g:A \rightarrow \{0,1\}$ correspond un unique sous ensemble $E_g=\{a, \in A, g(a) = 1\}$. Il y a donc une correspondance parfaite entre l'ensemble $\{0,1\}^A$ et l'ensemble $\mathcal P(A)$ qui d'ailleurs est parfois noté $2^A$. Coïncidence...? Dans ce monde étrange où tout, même les girafes, est un ensemble, 2 serait-il égal à ${0,1}$ ?

Entiers naturels

Enfin nous y voilà: les nombres dans ZFC.

A ce stade, vous ne serez pas surpris outre mesure d'apprendre que:

1. Ce sont des ensembles;
2. On peut les définir de plusieurs manières,
3. On trouve les bonnes descriptions en extrayant des entiers leur huile essentielle.

Quelles sont donc les propriétés essentielles des nombres ? En tout premier lieu, ils servent à compter. Ainsi, en -4000 av. J.-C., à Suse, pour comptabiliser un troupeau de 10 moutons, on plaçait 10 boules d'argile dans une enveloppe scellée: le nombre 10, c'est le point commun entre le troupeau de moutons et le contenu de l'enveloppe.

Ainsi, la 2-itude, c'est le point commun entre tous les ensembles de la forme $\{a,b\}$ avec $a\neq b$. Mais comment manier cette définition ? On ne peut pas parler de l'ensemble de toutes les paires dans ZFC (Russell et son barbier sanguinaire, tapis dans l'ombre, n'attendent que ça). On pourrait alors utiliser la prudente méthode habituelle: se donner un ensemble $X$ et regarder toutes les paires $\{a,b\}$ avec $a\neq b$, $a,b\in X$. Mais comment exporter notre notion de 2-itude en dehors de $X$ ?

Une solution serait de voir 2 comme une sorte d'unité de mesure, comme le mètre ou le kilogramme. Il s'agit alors de définir un 2 "standard", puis de trouver un moyen de le comparer avec d'autres ensembles pour vérifier leur 2-itude.

Tout à coup, cela semble beaucoup plus facile ! Il suffit de définir un 2 standard. Et un 3 standard. Et un 132247729394766 standard...

...ce qui pourrait prendre un moment. Mais a-t-on besoin de définir tous les nombres séparément ? Ne sont-ils pas, quand même, liés entre eux ? N'est-ce pas la raison pour laquelle "$\dots$" marche si bien ?

Supposons qu'on ait pris notre courage à deux mains et défini des standards jusqu'à 132247729394766 avant qu l'épuisement ne se fasse sentir. Comment passer au suivant ? Il faut ajouter un élément à l'ensemble 132247729394766. Puisque les éléments des ensembles sont eux-mêmes des ensembles, on peut tout simplement ajouter 132247729394766 lui-même.

Avant de sombrer dans un sommeil agité peuplé de nombres qui contiennent d'autres nombres, on définit ainsi le "successeur" $Sx$ d'un ensemble $x$ par

$$Sx = x \cup \{x\}$$

Et maintenant, on a réellement simplifié la tâche: il suffit de se donner un ensemble qui sera le standard pour zéro, et pour chaque entier, on sait maintenant passer au suivant. L'opération de passage au suivant est une opération tout à fait licite dans ZFC d'après les axiomes de la paire et de l'union. Or, il y a un candidat tout naturel pour 0: l'ensemble vide. On a donc:

$$0 =\emptyset$$ $$1 = S0= \emptyset \cup \{\emptyset\} = \{\emptyset\} = \{0\}$$ $$2 = S1 = \{\emptyset\} \cup \{\{\emptyset\}\}=\{\emptyset, \{\emptyset\}\} = \{0,1\} \text{ (Tiens donc})$$

...et ainsi de suite. Chaque entier $n$, en particulier, est égal à l'ensemble de ses prédecesseurs.

Comme précédemment, on peut aussi s'inquiéter de savoir si l'ensemble de tous les nombres est bien défini: fort commodément, il y a un axiome pour ça: l'axiome de l'infini nous donne un ensemble $I$ qui contient 0 ainsi que tous ses successeurs. Remarquons qu'on n'a pas encore $I=\mathbb N$: $I$ pourrait être beaucoup plus gros ! Mais comme toujours avec ZFC, se restreindre n'est pas le plus difficile. On peut le faire de deux façons différentes:

• Soit en utilisant l'axiome de compréhension avec la formule appropriée: en l'occurrence, on demande que chaque élément de $\mathbb N$ soit ou bien 0, ou le successeur de quelqu'un d'autre, et que tous les éléments de cet élément vérifient aussi cette propriété: $$\mathbb N:= \{n \in I, [n=\emptyset \text{ ou } \exists k, n=Sk] \text{ et } \forall m \in n[m= \emptyset \text{ ou } \exists k \in n, m=Sk]\}$$

  Toutefois, pour montrer que cela suffit à se restreindre aux entiers, il faut utiliser une méthode d'induction qui découle de l'axiome de fondation, et ça ne tombe pas tout seul.

• La deuxième méthode consiste à définir $\mathbb N$ comme l'intersection de tous les ensembles $I$ vérifiant: $$\emptyset \in I \text{ et } [x \in I \Rightarrow Sx \in I]$$ On obtient ainsi un ensemble caractérisé par le fait d'être contenu dans tous les $I$, et un tel ensemble est nécessairement unique. On peut donc lui donner un état civil dans ZFC, et le nommer $\mathbb N$.

Comme pour tous les objets définis sur cette page, les nombres que l'on vient de définir ont à la fois des propriétés que l'on veut, et des propriétés bizarres (par exemple $7 \in 8$). Comme pour les autres, on ignorera simplement ces possibilités exotiques, et on se contentera d'utiliser celles que l'on souhaite.

Conclusion

Avec des nombres et des fonctions, nos maths basées sur ZFC commencent à ressembler beaucoup plus à des maths. Il reste du chemin à faire: définir des opérations arithmétiques plus avancées que "j'ajoute 1", obtenir des ensembles de nombres qui permette de dépasser le décompte des moutons ($\mathbb Z, \mathbb Q$, voire, soyons fous, $\mathbb R$)...Mais les constructions déjà obtenues nous permettent tout de même de contempler ce projet avec un oeil optimiste et conquérant.

Référence: Naive Set Theory, par Paul Halmos.