Arithmétique de Peano
Cela fait tellement longtemps qu'on utilise les entiers, pour compter des choses, additionner, soustraire...que l'on se demande rarement pourquoi tout cela marche si bien, ou même, qu'est-ce qu'un entier. Ou pourquoi 2*3 (2 paquets de 3 pommes) devrait donner la même chose que 3*2, ou 3 paquets de 2 pommes. Commencer à se poser ce genre de question mène vite à des définitions circulaires (car l'intuition résiste quand on essaie de la chloroformer). On se retrouve rapidement à perdre le fil, et à avoir l'impression de ne plus rien savoir.
Dans ce post, on s'attachera à désapprendre ce que l'on a appris, et ensuite à reconstruire les nombres, par ordre croissant de sophistication: les entiers naturels, d'abord, afin d'être rassurés côté comptage de pommes, puis les entiers relatifs, les fractions, les réels, et les complexes. Pour cela, on utilise la méthode axiomatique. On se place donc dans le grand vide pré-Big Bang, et, ayant constaté qu'il est difficile de sortir quelque chose de rien, on cherche le minimum dont on doit disposer au départ pour pouvoir en déduire le reste, de la façon la plus économique possible (imaginons que le budget conceptuel est pas mal serré).
Les entiers naturels
On se demande donc, dans un premier temps ce que sont les entiers. Là, l'intuition sort de la cave où on a essayé de l'enfermer et s'exclame que c'est évident: on part de 0, et puis on compte, 1,2,3, et quand on se lasse, on dit "et ainsi de suite." Après lui avoir remis son bâillon, le démon du doute peut s'exprimer: comment garantir que, si on continue de compter assez longtemps, on ne va pas tourner en rond (retomber sur 0, par exemple ?) ? Et d'où sortent les opérations ?
Il est difficile de se débarasser de l'intuition qu'on a sur la nature même des nombres, que l'on acquiert à un très jeune âge (source), aussi pour éviter l'entorse au cortex préfrontal, penchons-nous d'abord sur les opérations. Avec des entiers naturels, on est en droit d'espérer additionner, multiplier et élever à des puissances entières (la soustraction et la division risquent de nous faire basculer dans l'Upside-Down des entiers relatifs ou pire, des fractions, aussi les ignorera-t-on pour le moment). Mais prendre une puissance entière, ce n'est jamais que multiplier plusieurs fois de suite; multiplier, ce n'est jamais qu'additionner plusieurs fois de suite: il semblerait que si on arrive à récupérer l'addition, les autres tombent toutes seules.
Encore plus économique: additionner, par exemple ajouter 34 à 2, ce n'est jamais qu'ajouter 1 34 fois de suite. Et on ne voit pas très bien comment on pourrait rogner encore plus. En fait, passer d'un nombre au suivant, c'est peut-être même ce qui caractérise les entiers: n'est ce pas ce que l'intuition essayait de dire tout à l'heure par "et ainsi de suite" ?
Un autre point intéressant soulevé par l'intuition, c'est qu'"on part de zéro". Pour pouvoir passer au suivant, il faut partir de quelque part. Il semble donc raisonnable de remplir un formulaire de demande de matériel pour nos deux concepts fondamentaux: l'entier 0 et l'opération "suivant" (ou "successeur"), notée $S$. On décrète donc:
Axiome 1: 0 est un entier naturel
et
Axiome 2: Si $n$ est un entier naturel, alors $S(n)$ aussi.
Comme $\overbrace{SS\dots S}^{42 \text{ fois }}0$ est un peu long, on donne à cet entier (les deux axiomes précédents nous garantissent que c'en est bien un) le nom "42", et de même on appelle "1" S(0), "2" S(S(0))...et il semble qu'avec ça, $\mathbb N$ soit l'ensemble formé par 0 et tous ses successeurs, euh, successifs, et c'est plié.
Mais pas si vite (glapit le démon du doute, en sortant de derrière un meuble) ! L'ensemble $\{0,1,2,3,4\}$, avec $S(4)=0$ sattisfait nos deux axiomes, et ne correspond pas du tout à ce que l'on veut. Notre système d'axiomes autorise que 5 soit égal à 0, ce qui n'est pas très satisfaisant.
De fait, c'est comme ça que les pendules fonctionnent (0h=12h); et aussi cette version évoluée que sont les ordinateurs. Sur un ordinateur, si on part de 0 et qu'on incrémente jusqu'à $2^{64}$, on finit par atteindre les limites de stockage de cette pauvre machine, qui alors revient à zéro. Mais dans l'espace abstrait où nous nous plaçons pour faire des maths, ce genre de considérations bassement matérielles ne devrait pas nous atteindre ! Pour empêcher la boucle, on décrète donc la propriété suivante de zéro, si évidente qu'on n'aurait pas penser devoir l'énoncer:
Axiome 3: 0 n'est le successeur d'aucun entier.
D'où le théorème, que l'on n'aurait pas cru trouver un jour si rassurant: 5 n'est pas égal à 0.
Mais le démon du doute hausse les épaules et dit, d'accord, mais $\{0,1,2,3,4\}$, avec $S(4)=4$ vérifie aussi cet axiome-là. Ou alors $S(4)=1$: on tourne en rond, en esquivant simplement 0. Pour pallier à ce problème, il nous faut une autre propriété "évidente" des entiers naturels: deux nombres différents ne peuvent pas avoir le même successeur. Ou encore, par contraposée:
Axiome 4: Pour tous entiers naturels $m$ et $n$, si $S(m) = S(n)$, alors $m=n$.
Ainsi, on garantit que tous nos entiers sont bien distincts. On a un autre théorème rassurant: 5 n'est pas égal à 4, et 6 n'est pas égal à 2. On regagne donc un optimisme prudent: il semble qu'on ait bien tous les entiers, sans boucles et sans redondance.
Mais...n'a-t-on que les entiers ? L'ensemble $\{0, 0.5,1,1.5,2,\dots\}$ vérifie également nos axiomes, et contient "trop" de nombres. En l'occurrence, on a les vrais entiers, plus une autre branche qui part de 0.5 et inclut tous ses successeurs...Comment élaguer cette branche indésirable ? Il va nous falloir un axiome plus fort, le principe de récurrence:
Axiome 5: Soit $P(n)$ un énoncé portant sur l'entier $n$. Si $P(0)$ est vraie, et que de plus, quand on a $P(k)$ alors $P(S(k))$ est aussi vraie, alors $P(n)$ est vraie pour tout entier $n$.
(Aparté: cette axiome diffère un peu des précédents: il ne porte pas "que" sur les entiers, mais aussi sur les propriétés des entiers; en fait, c'est une manière de produire un nouvel axiome pour chaque propriété des entiers. C'est donc ce que l'on appelle, dans le jargon, un schéma d'axiomes; mais la distinction nous intéresse peu ici.)
Prenons alors la propriété $P(n)$: "$n$ n'a pas de chiffre après la virgule". Alors $P(0)$ est vraie, et si $P(k)$ est vraie pour un entier $k$, alors $P(S(k))$ aussi. Alors notre dernier axiome nous garantit que $P(n)$ est vraie pour tout entier. Mais $P(0.5)$ n'est pas vraie; donc 0.5, et tous ses successeurs d'ailleurs, ne sont pas des entiers. (Cette histoire de virgule est un peu floue, on n'a pas parlé du système décimal, ni défini de virgules ou de telles horreurs; le but est simplement d'illustrer comment le principe de récurrence nous permet de ne garder que les "bons" objets dans notre candidat $\mathcal N$.)
Evidemment, ce n'est pas le seul intérêt de cet axiome: il nous permet aussi et surtout de faire marcher les preuves par récurrence, sans lesquelles prouver des théorèmes d'arithmétique serait un peu long.
Grâce aux axiomes 1 à 5 (les axiomes de Peano de l'arithémtique), il semble qu'on ait récupéré les entiers, tous les entiers, et rien que les entiers, avec en bonus l'opération d'incrémentation (et le démon du doute existentiel est retourné se cacher quelque part pour sortir dramatiquement plus tard, ce qui est bon signe). Pour cimenter la chose, on se fait livrer directement de la théorie des ensembles:
Axiome: Il existe un ensemble qui vérifie les axiomes de Péano.

Remarquons qu'on a pas exactement décrit de quoi les entiers sont faits: on a simplement extirpé les propriétés qui les caractérisent, sans lesquelles il serait déraisonnable de parler d'entiers. Cette caisse qui tombe du ciel (plus précisément, de la théorie des ensembles ZFC) et nous donne $\mathbb N$ est un indice: on peut construire les entiers en se ramenant à des objets encore plus fondamentaux: les ensembles. Mais on pourrait alors se demander de quoi les ensembles sont faits...La méthode axiomatique est une façon de reconnaître qu'il faut bien partir de quelque chose (dans les maths classiques, justement, on part des ensembles: plus de détails ici et là), et que, quelle que soit la manière dont on y parvient, tout ce qui vérifie ces axiomes mérite d'être traité comme un entier.
Arithmétique
On va maintenant s'attacher à redonner à l'arithmétique la tête qu'on lui connaît, avec les opérations d'addition (et non simplement d'incrémentation) et de multiplication. Ce sera l'occasion d'illuster la puissance de notre 5ème axiome, le principe de récurrence, qui nous permet de poser des définitions inductives: si on sait ce qu'une certaine opération fait à 0, et si on sait déduire ce qu'elle fait à $S(n)$ à partir de ce qu'elle fait à $n$, alors on "connaît" complètement ladite opération.
Addition: Soit $m$ un entier naturel. On définit l'opération "ajouter $m$", notée (temporairement) $a_m$ par
- $a_m(0) = m$;
- $a_m(S(n))= S(a_m(n)).$
On notera par la suite $s_m(n) = n+m$.
On montre alors, par récurrence, que $n+m$ est bien un entier pour tout entier $n$:
- Initialisation: puisque $m$ est un entier, et que $0+m=m$, on a bien que $0+m$ est un entier.
- Hérédité: Supposons que l'on ait montré que $n+m$ est un entier, et montrons que $S(n)+m$ est aussi un entier. Par définition, $S(n)+m=a_m(S(n))=S(a_m(n))= S(n+m)$. Par l'axiome 2, puisque $n+m$ est entier, $S(n+m)$ aussi.
On peut avoit furieusement l'impression, dans ce genre de preuve, d'enfoncer des portes ouvertes. Il est important de noter, au cas où l'intuition aurait des velléités de s'exprimer, qu'à ce stade, on ne sait encore pas grand chose de notre opération d'addition. En particulier, il ne découle pas directement de la définition que $n+m = m+n$ (ce qui semble moins évident si on l'écrit $a_m(n)= a_n(m)$), ou encore que $(n+m)+p=n+(m+p)$ (c'est-à-dire, $a_p(a_m(n))=a_{a_p(m)}(n)$). Que l'on se rassure, toutefois: ces propriétés sont bien vérifiées. On a:
- L'addition est commutative: pour tous entiers $m$ et $n$, $m+n=n+m$.
- L'addition est associative: pour tous entiers $m,n$ et $p$, $(n+m)+p=n+(m+p)$
- Simplification: pour tous entier $m, n$ et $p$, si $m+n=m+p$ alors $n=p$.
- Si $m+n=0$ alors $m=0$ et $n=0$.
Les preuves, sans grande surprise, se font par récurrence et, avec surprise de taille moyenne, sont en fait assez longues ! Démontrer des choses évidentes donne lieu à un mélange inimitable de frustration et de satisfaction, aussi je vous encourage à essayer, mais sinon, vous trouverez des détails ici.
Savoir additionner, outre une certaine utilité, paraît-il, quand on fait ses courses, va nous servir de tremplin pour récupérer d'autres opérations fondamentales: l'ordre, la multiplication et la division euclidienne.
Ordre:Soient $m$ et $n$ deux entiers naturels. On dira que $n$ est supérieur ou égal à $m$, noté $m \leq n$, si $n=m+p$ pour un certain entier $p$. Si de plus $n \neq m$, on note $m< n$.
Remarquons que pour tout $n$, on a donc $n< S(n)$: il n'y a donc pas de plus grand entier. Comme pour l'addition, les propriétés évidentes de l'ordre ne le sont en fait pas tant que ça, mais on récupère tout de même sans trop de douleur:
- L'ordre est réflexif: pour tout entier $m$, $m \leq m$.
- L'ordre est transitif: pour tous entiers $m,n$ et $p$, si $m \leq n$ et $n\leq p$ alors $m \leq p$.
- L'ordre est anti-symétrique: pour tous entiers $m$ et $n$, si $m\leq n$ et $n\leq m$ alors $m=n$.
- L'addition préserve l'ordre: pour tous $m$,$n$ et $p$, $m \leq n$ si et seulement si $m+p \leq n+p$.
- Pour tous $m$ et $n$ entiers, une et une seule des propriétés suivantes est vraie: $m< n$, $m=n$ ou $n< m$.
Multiplication: Soit $m$ un entier. On définit l'opération "multiplier par $m$", notée $f_m$, par:
- $f_m(0) = 0$
- Pour tout entier $n$, $f_m(S(n))= f_m(n)+m$.
On notera $f_m(n)= n \times m.$ (Comme pour l'addition, la notation $f_m$ a surtout pour utilité d'aider à assommer l'intuition).
On a donc $0 \times m = 0$, $1 \times m = S(0) \times m = 0 + m = m$, $2 \times m = S(1) \times m = 1\times m + m = m+m$. La multiplication semble bien faire ce que l'on veut qu'elle fasse, et on a bien les propriétés convenables:
- La multiplication est commutative: $m\times n = n \times m$.
- La multiplication est associative: Pour tous entiers $m,n$ et $p$, $m\times (n\times p) = (m\times n)\times p$.
- Si $m\times n = 0$ alors soit $m=0$ soit $n=0$.
- Loi de distribution: Pour tous entiers $m,n$ et $p$, $m\times (n+p) = m\times n + m\times p$.
- La multiplication préserve l'ordre: si $m < n$ et si $p \neq 0$, alors $m \times p < n \times p$.
- Simplification: si $p \neq 0$ et $m \times p = n \times p$ alors $m=n$.
Division:Soient $m$ et $n$ deux entiers. Alors il existe $q$ et $r$ entiers, tels que $0 \leq r < m$ et $n = m\times q +r$. On dit que $q$ est le quotient de la division de $n$ par $m$, et $r$ le reste.
Entiers relatifs
On aimerait maintenant pouvoir soustraire un entier à un autre, mais si on le fait sans précaution, cette opération risqie de nous sortir de notre ensemble durement acquis des entiers naturels. On va donc l'étendre pour inclure des entiers négatifs, et ceci fait, on pourra soustraire à coeur joie.
Puisque le but est de pouvoir soustraire, on va définir les entiers relatifs comme les résultats de toutes les soustractions $m-n$ possibles, avec $m$ et $n$ des entiers naturels. Deux problèmes se posent: on n'a pas encore donné de sens au signe "-", et de plus, deux soustractions différentes peuvent donner le même résultat; ainsi $6-3=8-5$.
Comme précédemment, on va utiliser l'intuition pour poser une définition, puis l'assommer aussitôt à coup de notations étranges pour pouvoir travailler. Ainsi, on va considérer qu'un entier relatif est un couple $(m,n)$ d'entiers naturels (que l'on notera $m_n$); et on dira que $(m,n)$ et $(a,b)$ sont égaux si $m+b=a+n$ (Pourquoi ?). On appellera $\mathbb Z$ l'ensemble des entiers relatifs; ainsi, on s'est ramenés à des propriétés que l'on connait déjà sur des objets que l'on connaît déjà.
Une remarque: Dans ce genre de cas, où l'on a des "noms" différents qui désignent "la même chose", (ici par exemple (6,3) et (8,5), dont on veut qu'ils désignent 3), on est souvent amenés à poser une condition ad hoc d'égalité, notée par exemple $\simeq$; pour que tout se passe bien, cette condition doit vérifier trois propriétés raisonnables:
- Un couple d'entier doit être "égal" à lui-même: Pour tous entiers $m$ et $n$, $(m,n) \simeq (m,n)$;
- Si $(m,n) \simeq (a,b)$, alors on veut que $(a,b) \simeq (m,n)$;
- Si $(m,n) \simeq (p,q)$, et $(p,q)\simeq (a,b)$, alors on veut que $(m,n) \simeq (a,b).$
Dans ce cas, on dit que $\simeq$ est une relation d'équivalence. On peut vérifier que c'est bien le cas ici. On commettra cependant constamment l'abus de langage qui consiste à utiliser indifféremment "$=$" et "$\simeq$".
Par exemple, avec cette définition, (2,5) est un entier relatif égal à (0,3) (ou encore 2-5 = 0 -3, ce qui paraît raisonnable). Ce qui paraît moins raisonnable, c'est que les entiers naturels, par cette définition, ne sont pas des entiers relatifs ! On peut toutefois contourner le problème en décidant que, lorsqu'il passe la frontière du royaume de $\mathbb Z$, l'entier $p$ s'appelle $(p,0)$. Remarquons que $(0,p)$ correspond alors à ce qu'on a envie d'appeller $-p$. En fait, pour tout entier relatif $(m,n)$, il existe $p \in \mathbb N$ tel que
On laisse temporairement l'intuition s'exprimer de nouveau pour étendre à $\mathbb Z$ les opérations disponibles sur $\mathbb N$:
- Addition: On pose $(m,n)+(a,b):=(m+a,n+b)$. Ainsi, $(2,5)+(3,0)=(2+3,5+0)=(5,5)\simeq(0,0)$.
- Multiplication: On pose $(m,n)\times (a,b):=(m\times a + n \times b, m \times b + n \times a)$. Ainsi, $(1,3) \times (2,0) = (2,6) \simeq (0,4)$.
Tout ceci semble bien marcher, mais il faut tout de même vérifier que ces opérations sont compatibles avec notre étrange égalité $\simeq$: si $(\tilde m, \tilde n) \simeq (m,n)$ alors on doit avoir $(m,n)+(a,b) = (\tilde m, \tilde n)+(a,b)$ et $(m,n)\times (a,b) = (\tilde m, \tilde n)\times (a,b)$. Cette vérification est laissée en exercice.
Les propriétés qe l'on a déjà démontrée sur les entiers naturels permettent alors de montrer que si $x=(m,n)$, $y=(p,q)$ et $z=(a,b)$ sont trois entiers relatifs, on a:
$$ \begin{align} x+y &= y+x \\ (x+y)+z &= x+(y+z)\\ x+(0,0) &= x \\ x \times y = y \times x \\ (x\times y)\times z &= x\times (y\times z)\\ x \times (1,0) &= x \\ x \times (0,0) &=(0,0)\\ x \times (y+z) &= x \times y + x \times z \end{align} $$Par exemple,
$$ \begin{align} x \times (y+z) &= (m,n)\times ((p,q)+(a,b))\\ &=(m,n)\times (p+a,q+b) \\ &=(m\times (p+a) + n \times (q+b), n \times(p+a)+ m \times (q+b))\\ &=(mp+ma+nq+nb,np+na+mq+mb), \text{ et }\\ x\times y + x \times z &= (m,n)\times(p,q) + (m,n)\times (a,b)\\ &= (mp+nq, mq +np)+(ma+nb, mb + na)\\ &=(mp+nq+ma+nb,mq+np+mb+na). \end{align} $$De plus, si $x \times y = (0,0)$, alors $x=(0,0)$ ou $y =(0,0)$; d'où l'on déduit que si $z$ est non nul, et $x \times z = y \times z$ alors $x=y$.
Pour tout entier relatif $(m,n)$, on définit son opposé par $-(m,n)= (n,m)$. On vérifie, là aussi, que cette opération est compatible avec $\simeq$. On a alors, pour tout $(m,n)$, $(m,n) + (-(m,n))=(m+n, m+n) \simeq (0,0)$ ce qui correspond bien à l'idée qu'on se fait d'un opposé. De plus,
- Soit $(m,n)$ correspond à un entier naturel (non nul) $p$, i.e $(m,n)\simeq(p,0)$; dans ce cas, on dit que c'est un entier (strictement) positif
- Soit $(m,n)$ est "égal" à 0: $(m,n)\simeq (0,0)$;
- Soit $-(m,n)$ correspond à un entier naturel (non nul) $p$, i.e $(n,m)\simeq(p,0)$; dans ce cas, on dit que c'est un entier (strictement) négatif.
Remarquons que par cette définition, si l'on prend deux entiers négatifs $x \simeq (0,p)$, $y \simeq (0,q)$ alors $x \times y \simeq (0\times 0 + p \times q, 0\times p + q \times 0) = (pq, 0)$: le produit de deux négatifs est un positif.
Grâce à cette notion de positivité, on étend l'ordre aux entiers relatifs: pour $x$, $y$ dans $\mathbb Z$, on dit que $x$ est (strictement) plus grand que $y$ s'il existe un entier relatif (strictement) positif $z$ tel que $y=x+z$ (et on utilise la notation usuelle).
On est alors équipés pour définir la substraction!
Sans grande surprise, on pose, pour $x=(m,n)$ et $y=(p,q)$ deux entiers relatifs,
Remarquons que si $x=(p,0)$ et $y=(q,0)$ sont associés à des entiers naturels, alors $x-y = (p,q)$, ce que l'on "interprète" depuis le début comme $p-q$; il semble donc que notre construction des entiers relatifs soit à peu près cohérente, et en tout cas passe le test du canard.
Rassurés, on va "oublier" la définition sous forme de couple d'entiers naturels, et noter simplement $(p,0)$ par $p$, $(0,p)$ par $-p$ et $(0,0)$ par 0, et se passer de $\simeq$.
Rationnels
Il ne nous reste qu'une opération à ajouter à notre menu: la division (celle qui donne des fractions). On va donc s'essayer à reconstruire les rationnels. A la lumière de ce qui a si bien marché pour les entiers relatifs, on voit que pour construire un élément de $\mathbb Q$, il nous faut deux éléments $[x,y]$ de $\mathbb Z$(qui donneront bien sûr $\frac xy$), avec $y \neq 0$, et une nouvelle "égalité" bizarre: $[x,y] \cong [z,t]$ si $x \times t = y \times z$. On appelle $\mathbb Q$ l'ensemble ainsi construit.
Par exemple, $[-3,4] \cong [6,-8]$. On vérifie de plus que notre nouvelle "égalité"" $\cong$ vérifie bien les propriétés requises pour une relation d'équivalence. Comme toujours, on libère brièvement l'intuition de ses menottes, le temps d'étendre les opérations d'addition(/soustraction) et de multiplication à $\mathbb Q$:
- Addition: Soient $[p,q]$ et $[a,b]$ deux rationnels, alors on définit $[p,q] + [a,b] = [(p\times b+a \times q), b \times q]$. Remarquons que (on l'a montré!) puisque $q$ et $b$ sont non nuls, $q\times b$ est aussi non nul, et la somme est donc bien définie.
- Multiplication: $[p,q]\times [a,b]=[p\times a, q \times b]$
- Opposé: On définit l'opposé de $[p,q]$ par $-[p,q]=[-p,q]$.
Comme pour les entiers relatifs, il faut vérifier (c'est un très bon entraînement) que ces définition sont compatibles avec $\cong$. Remarquons aussi que si le dénominateur est égal à 1, on récupère les règles opératoires sur les entiers relatifs:
$$ \begin{align} [a,1] + [b,1] &= [a+b,1]\\ [a,1] \times [b,1] &=[a\times b, 1]\\ -[a,1] &= [-a, 1] \end{align} $$Ce qui nous permet, d'un petit saut conceptuel par dessus le ruisseau des pesantes définitions, de considérer $\mathbb Z$ comme sous-ensemble de $\mathbb Q$, de même que l'on avait plongé $\mathbb N$ dans $\mathbb Z$. Ainsi, par abus de langage, on notera par exemple 1 le rationnel $[1,1]$.
Suivant toujours le modèle de la construction de $\mathbb Z$, on définit l'inverse d'un rationnel $x=[a,b]$ non-nul (c-à-d, $a\neq 0$) par $x^{-1}=[b,a]$ (on notera aussi $1/x$). On a alors $x \times x^{-1} \cong 1$. De là, on définit l'opération de division d'un rationnel par un autre, sans surprise, par:
$$x /y = x \times y^{-1}$$On vérifie que la division des entiers a bien le comportement requis: en notant $2=[2,1]$, $3=[3,1]$, on a:
$$2 / 3 = [2,1] \times [3,1]^{-1}=[2,1] \times [1,3] = [2,3],$$que l'on comprend comme $\frac 23$.
On étend enfin la notion d'ordre aux rationnels. On dira que $x \in \mathbb Q$ est (strictement) positif s'il existe $a, b \in \mathbb Z$ (strictement) positifs tels que $x \cong [a,b]$. On dira que $x \in \mathbb Q$ est (strictement) négatif s'il existe $y \in \mathbb Q$ (strictement) positif tel que $x = -y$. On vérifie alors que tout rationnel est soit positif, soit nul, soit négatif. Du coup, pour $x$, $y$ deux rationnels, on dira que $x$ est (strictement) plus grand que $y$ si $x-y$ est un rationnel (strictement) positif.
Comme toujours, les rationnels, ou du moins quelque chose qui y ressemble furieusement, ayant été reconstruits, on peut laisser l'intuition sortir de sa cage; on notera à nouveau $\frac pq$ au lieu de $[p,q]$, et autres simplifications salutaires.
Trous dans les rationnels
On a donc récupéré les quatres opérations de base (dont se déduisent d'autres, dont je n'ai pas parlé ici, comme l'exponentiation ou la valeur absolue), ainsi que l'ordre. On est donc en mesure d'acheter des papayes et des DVD, de savoir combien on a payé au total et par article, et de comparer avec ses petits camarades. Les promesses des instituteurs sur l'utilité quotidienne (ou hebdomadaire... ou annuelle) des mathématiques ont été tenues !
Mais si l'on souhaite faire de "vraies" mathématiques, comme ça:
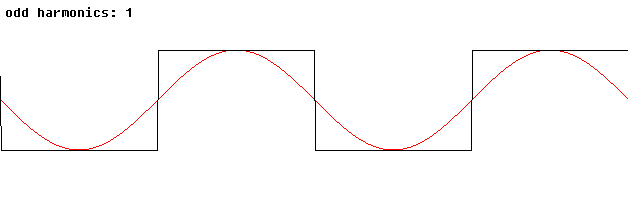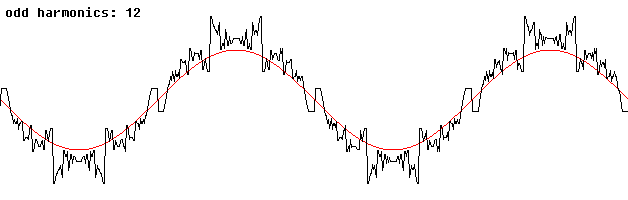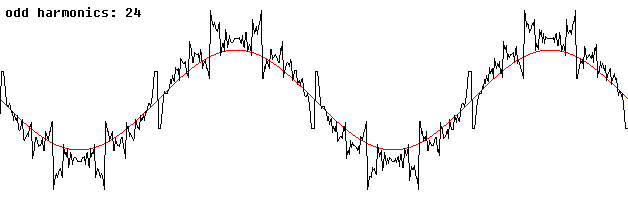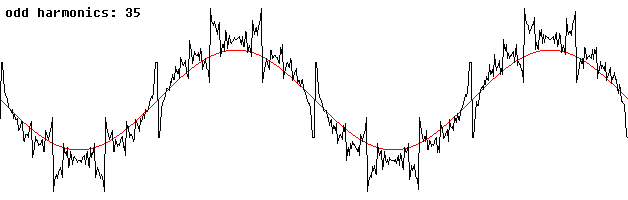

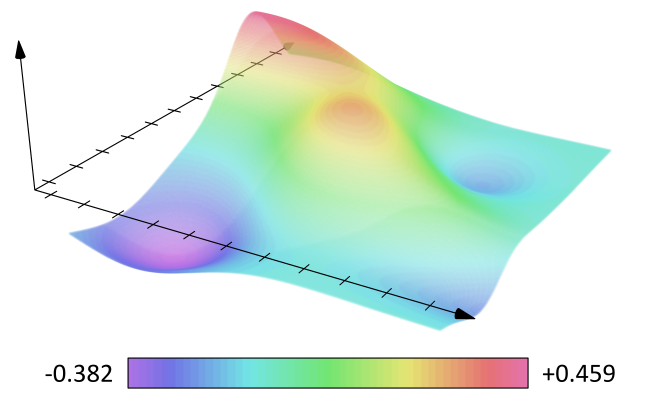
...on va rapidement s'apercevoir qu'il manque des choses. Tout d'abord, parce qu'il existe des nombres, conceptuellement pas très compliqués, dont notre construction ne nous permet pas de parler. Par exemple, on peut montrer, de moult manières, que la diagonale d'un carré de côté 1 ($\sqrt 2$ pour les intimes), ne peut pas s'écrire sous la forme d'un rationnel $\frac pq$. De même pour le périmètre d'un cercle de rayon 1 ($2\pi$, ou $\tau$ pour les intimes).
Cette fois, ce qui nous manque n'est pas une opération particulière. On pourrait dire qu'on veut ajouter les racines carrées, mais ça ne nous rendra pas $\pi$: c'est la distinction entre les nombres dits algébriques et ceux dits transcendants, dont on reparlera dans un autre post. Qui arrive. Dans 8 saisons.
Ce qui nous manque ici, donc, est une notion plus...subtile.
Puisqu'on a un ordre, on peut imaginer aligner tous les nombres obtenus jusqu'ici par ordre croissant pour inspection. Et là, le problème apparaît plus clairement: il y a des trous !
Essayons d'obtenir une prise plus sûre de cette histoire de trous. Commençons par observer que des rationnels, il y en a quand même un paquet: contrairement à ce que suggère l'animation ci-dessus, entre deux rationnels, on peut toujours en intercaler un troisième. Autrement dit, si $x$ et $y$ sont deux rationnels tels que $x< y$, alors il existe $z \in \mathbb Q$ tel que $x< y< z$ (par exemple, $z = (x+y)/2$). On peut donc "zoomer" autant qu'on veut, on ne tombera jamais à court de rationnels: et pourtant, il manque des nombres, par exemple $x$ tel que $x^2=2$. (On va éviter de parler de $\sqrt{2}$ puisque, techniquement, on ne l'a pas construit).
Mais même si un tel nombre ne peut pas s'écrire sous la forme $\frac pq$, on peut l'"approcher" avec des éléments de $\mathbb Q$; ou, de façon équivalente, on peut approcher 2 avec des carrés de rationnels (ce qui nous évite de parler de $\sqrt 2$ dont, encore une fois, on n'a pas vraiment montré qu'il existait). Plus précisément, pour tout écart $\delta$ rationnel, si petit soit-il, il existe $x \in \mathbb Q$ tel que $x^2 < 2 < (x+\delta)^2$.
En effet, prenons un petit $\delta$ et supposons, par l'absurde, qu'un tel $x \in \mathbb Q$ n'existe pas. Autrement dit, pour tout rationnel $\delta$, si $x^2 < 2$ alors $(x+\delta)^2$ aussi est plus petit que 2. En particulier, puisque $0^2 < 2$, on aurait alors $\delta^2 < 2$. Mais alors $\delta$ est un rationnel tel que $\delta^2 < 2$; donc, pour $x=\delta$, on a $(x+\delta)^2= (2\delta)^2 < 2$. D'un coup de "etc", on en déduit que pour tout entier naturel $n$, $(n\delta)^2 < 2$. Mais des entiers naturels, on s'en est assurés, il y en a une infinité, et on peut même montrer que pour n'importe quel rationnel $a$, il existe un entier strictement plus grand que $a$. En particulier, il existe un entier, tellement grand qu'on va le noter $N$ majuscule, tel que $N > 2/ \delta$. Alors $(N\delta)^2 > 4$, ce qui contredit notre précédente affirmation que, pour tout entier naturel $n$, $(n\delta)^2 < 2$. C'est une contradiction, et donc, l'hypothèse de départ, selon laquelle le $x$ désiré n'existait pas, est fausse. CQFD.
Ce que l'on en tire, c'est que même si aucun rationnel $x$ ne vérifie $x^2 = 2$, certains ne sont "vraiment pas loin" d'un nombre hypothétique qui vérifierait cette équation. En prenant, pour chaque entier $n$, $\delta = 1 / 10^n$, on obtient alors un rationnel $x_n$ qui est "proche" de cette hypothétique racine de 2 à $0.\underbrace{00\dots 0}_{n \text{ fois }}1$ près. On n'a pas parlé ici d'écriture décimale des nombres, mais une telle suite de rationnel pourrait être:
$$x_0 = 1,\ x_1= 1.4, \ x_2= 1.41,\ x_3= 1.414,\dots$$Il semble donc qu'on pourrait obtenir les nombres manquants par un procédé de "limite", qui nous permettrait de préciser ce "..."" pour mieux comprendre ce qui se passe "à l'infini". Mais c'est une autre histoire, qui sera racontée une autre fois !
