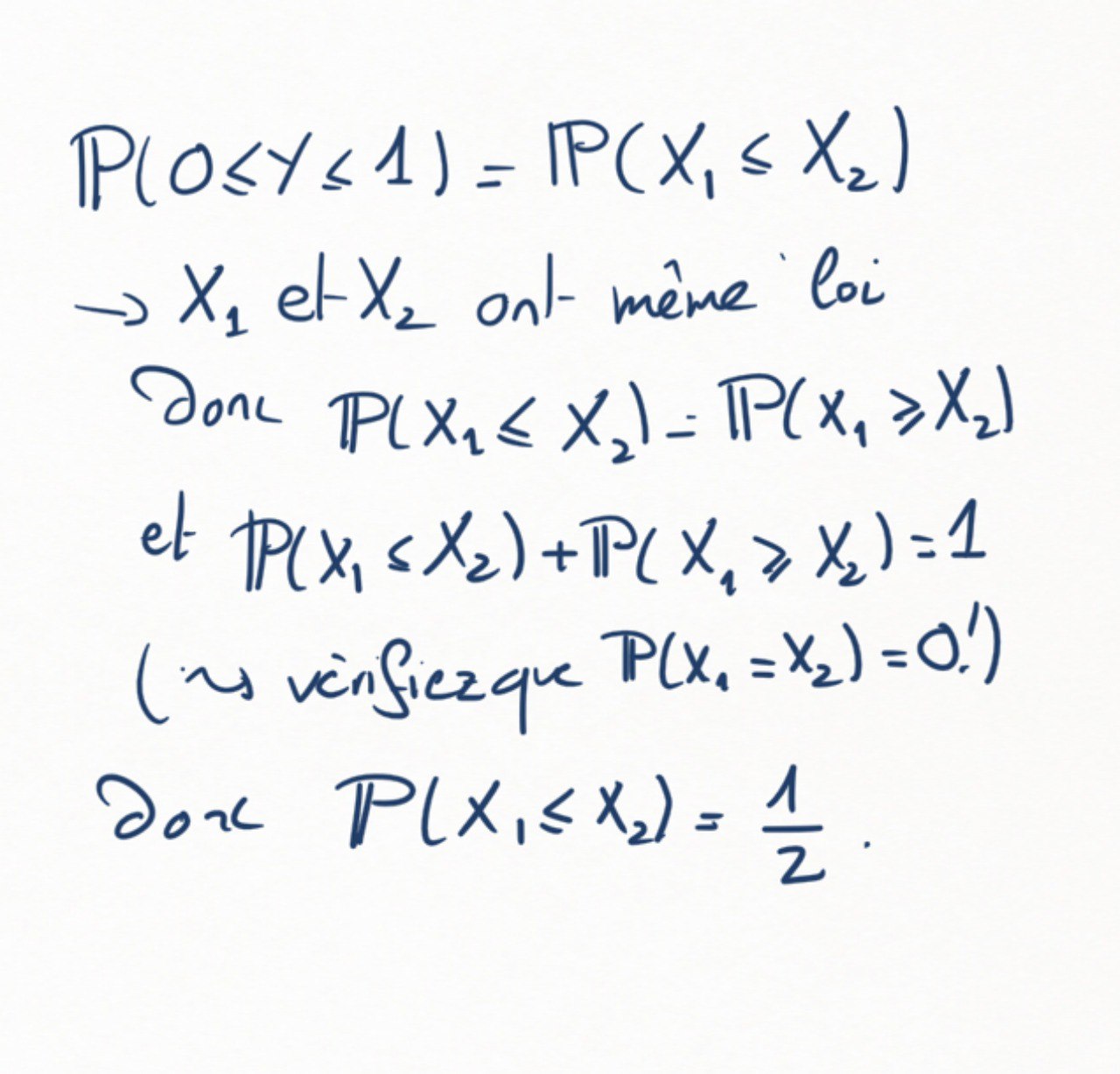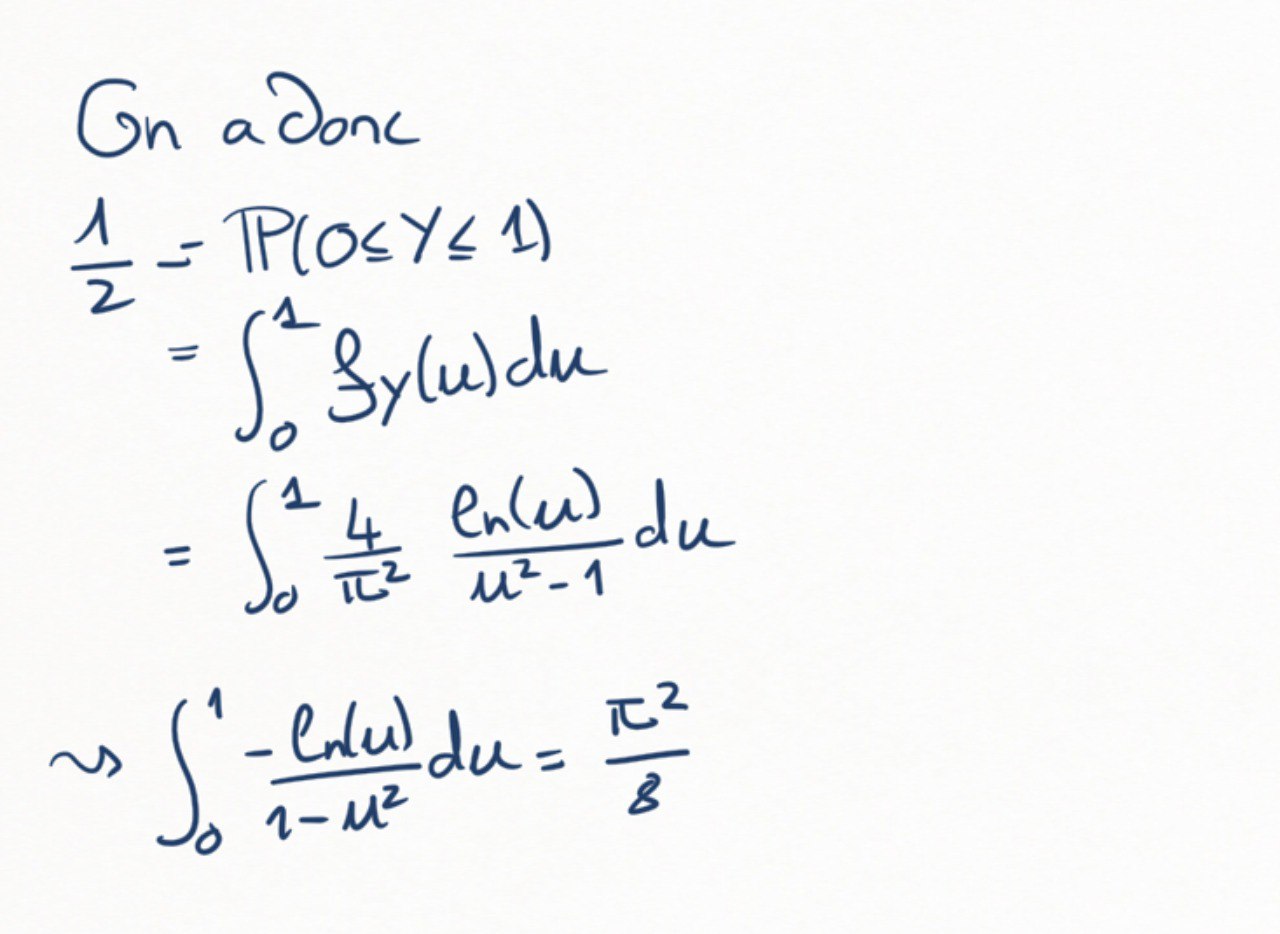Section 4 Une dernière pour la route: avec des probas
On peut aussi démontrer cette formule avec des probabilités.
Projet 4.1.
(a)
Soient \(X_1,X_2: \mathbb R \rightarrow \mathbb R^+\) deux variables aléatoires positives suivant la (demi-) loi de Cauchy 1 . Leur densité de probabilité est donc
\begin{equation*}
f_{X_1}(t)=f_{X_2}(t)=
\begin{cases}
\frac2{\pi}\frac1{1+t^2} \amp\text{ si } t>0\\
0 \amp\text{ si } t \leq0
\end{cases}
\end{equation*}
Posons \(Y=\frac{X_1}{X_2}\text{.}\) Montrer que la densité de \(Y\) est donnée par
\begin{equation*}
f_Y(u)=\int_0^\infty tp_{X_1}(tu)p_{X_2}(t)dt
\end{equation*}
(b)
En déduire que
\begin{equation*}
f_Y(u)=\frac{4}{\pi^2}\frac{\ln(u)}{u^2-1}
\end{equation*}
Indication.
Trouver deux réels \(a\) et \(b\) tels que
\begin{equation*}
\frac1{1+t^2u^2}\frac1{1+t^2} = \frac{a}{1+t^2u^2}+\frac{b}{1+t^2}
\end{equation*}
(c)
Justifier que \(\mathbb P(0\leq Y\leq 1) = \frac12\text{.}\) En déduire que
\begin{equation*}
\int_0^1 -\frac{\ln(u)}{1-u^2} du = \frac{\pi^2}8
\end{equation*}
(d)
De là, montrer que
\begin{equation*}
\sum_{n=0}^\infty \frac1{(2n+1)^2} =\frac{\pi^2}8
\end{equation*}
Indication.
Pour \(u\in ]0,1[\text{,}\) on a
\begin{equation*}
\frac1{1-u^2}= \sum_{k=0}^\infty u^{2k}
\end{equation*}
(e)
En déduire que
\begin{equation*}
\sum_{n=1}^\infty \frac1{n^2} = \frac{\pi^2}6
\end{equation*}
Indication.
En séparant les entiers pairs et impairs, montrer que, en notant \(S=\sum_{n=1}^\infty \frac1{n^2}\text{,}\)
\begin{equation*}
S=\frac14 S + \sum_{n=0}^\infty \frac1{(2n+1)^2}
\end{equation*}
Puisque la série \(\sum \frac1{n^2}\) converge, on peut écrire:
\begin{equation*}
S=\sum_{n=1}^\infty \frac1{n^2} = \sum_{k=1}^\infty \frac 1{(2k)^2} + \sum_{k=0}^\infty \frac 1{(2k+1)^2}
\end{equation*}
Or, pour tout \(k\geq 1\text{,}\) \(\frac 1{(2k)^2} = \frac14 \frac{1}{k^2}\) donc
\begin{equation*}
\sum_{k=1}^\infty \frac 1{(2k)^2} = \frac14\sum_{k=1}^\infty \frac 1{k^2} = \frac14 S
\end{equation*}
donc
\begin{align*}
\frac 34 S \amp = \sum_{k=0}^\infty \frac1{(2k+1)^2}\\
S \amp= \frac34 \sum_{k=0}^\infty \frac1{(2k+1)^2} \\
\amp = \frac43 \frac{\pi^2}{8}=\frac{\pi^2}{6}
\end{align*}
distribution-explorer.github.io/continuous/halfcauchy.html