Skip to main content

Section 3 Preuve du théorème des fonctions implicites

On s'intéresse à une fonction \(\mathcal C^1\)

\begin{equation*} f: U \subset E\times F \rightarrow G \end{equation*}

où \(E,F,G\) sont trois espaces de Banach, et plus précisément, on veut décrire l'ensemble

\begin{equation*} \mathcal Z=\{(x,y)\in U,\ f(x,y)=0_G\} \end{equation*}

au voisinage d'un point \((x_0,y_0)\text{.}\)

Encore plus précisément, on souhaite réécrire cet ensemble comme le graphe d'une fonction \(\varphi: V \rightarrow W\text{,}\) \(\mathcal C^1\text{,}\) définie sur un voisinage \(V\) de \(x_0\) et à valeurs dans un voisinage \(W\) de \(y_0\text{:}\)

\begin{equation*} \mathcal Z=\{(x,y)\in V\times W,\ y=\varphi(x)\} \end{equation*}

Dans ce but, on introduit quelques notations:

Pour \((x_0,y_0)\in U\text{,}\) on note:

  • \(D_x f(x_0,y_0) \in \mathcal L(E,G)\) la différentielle de l'application \(x\mapsto f(x,y_0)\text{,}\)

  • \(D_y f(x_0,y_0) \in \mathcal L(F,G)\) la différentielle de l'application \(y\mapsto f(x_0,y)\text{.}\)

Montrer que, pour tout \((x_0,y_0)\in U\) et pour tout \((h,k)\in E \times F\text{,}\)

\begin{equation*} Df(x_0,y_0)(h,k) = D_x f(x_0,y_0)(h) + D_yf(x_0,y_0)(k) \end{equation*}

Si \(E=\R^n, F=G=\R^p\text{,}\) ceci revient à décomposer la jacobienne de \(f\) en deux parties:

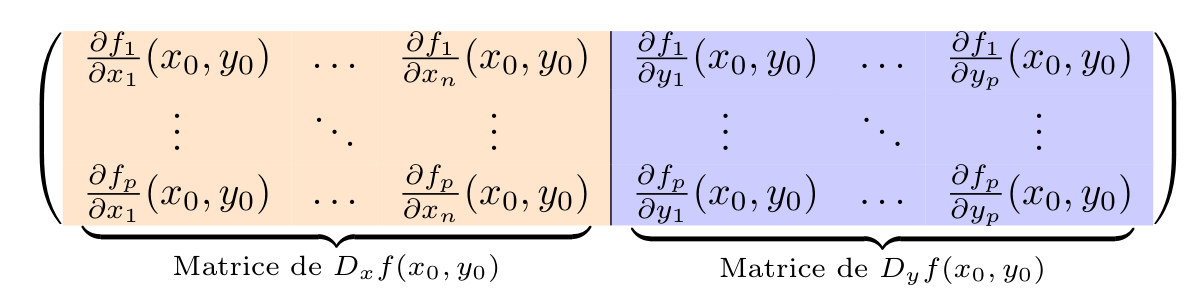
On a donc, pour \((h,k)\in \R^n\times \R^p\text{,}\)

\begin{align*} Df(x_0,y_0)(h,k)\amp=\sum_{i=1}^n \textcolor{orange!80!black}{\frac{\del f}{\del x_i}(x_0,y_0)} h_i + \sum_{i=1}^p \textcolor{blue!80!black}{\frac{\del f}{\del y_i}(x_0,y_0)} k_i\\ \amp =\textcolor{orange!80!black}{D_xf(x_0,y_0)}(h)+\textcolor{blue!80!black}{D_yf(x_0,y_0)}(k). \end{align*}

Le théorème qui précise quand on peut décrire l'ensemble des zéros de \(f\) comme le graphe d'une fonction \(\varphi\) s'appelle le théorème des fonctions implicites:

On va démonter ça en utilisant le TIL avec une fonction bien choisie:

  • Etape 1: Choix de la fonction: On pose

    \begin{align*} g : U \subset E\times F \amp \rightarrow E \times G\\ (x,y)\amp \mapsto (x,f(x,y)) \end{align*}

    On vérifie que \(g\) est différentiable et \(\C^1\) sur \(U\text{,}\) et on détermine \(Dg(u_0)\text{.}\)

  • Etape 2: On montre qu'on peut appliquer le TIL à \(g\text{:}\)

    • D'abord, pour se faire une idée, on se place dans le cas où \(E=\R^n,F=G=\R^p\text{.}\) On détermine l'allure de \(\Jac\, g(u_0)\) et on en déduit que \(\det (\Jac\, g(u_0))\neq 0.\)

    • Dans le cas général, on montre que \(Dg(u_0)\) est un isomorphisme linéaire.

  • Etape 3: On applique le TIL à \(g\) en \(u_0\text{:}\) ça nous donne un voisinage \(\tilde U\) de \(u_0\) tel que

    \begin{equation*} g_{|\tilde U}:\tilde U \rightarrow g(\tilde U) \end{equation*}

    est un \(C^1\)-difféomorphisme.

    Il s'agit alors de faire de l'ajustement de voisinage pour en déduire les \(V,W\) et \(\varphi\) qu'on cherche.

  • Etape 4: On calcule la différentielle de \(\varphi\text{.}\)

Exercice A la recherche de la fonction implicite

On introduit la fonction

\begin{equation*} g:(x,y)\in U\subset E\times F \mapsto (x,f(x,y))\in E\times G \end{equation*}

L'équation qu'on essaie de résoudre devient

\begin{equation*} f(x,y) = 0_G \iff g(x,y)=(x,0_G) \end{equation*}

1. Etape 1.

On va commencer par déterminer la différentielle de \(g\text{.}\)

Dans un premier temps, plaçons-nous dans un cas simple: on suppose que \(E=\R^n,F=G=\R^p.\)

Justifier que \(g\) est \(C^1\) sur \(U\) et déterminer \(\Jac g(u)\text{,}\) pour \(u\in U\text{.}\)

Spoiler.

2.

Dans le cas général où \(E,F,G\) sont des espaces de Banach mystère, s'assurer que \(g\) est toujours \(C^1\) sur \(U\) et déterminer \(Dg(u)(h)\) pour \(u=(x,y)\in U\) et \(h=(h_1,h_2)\in E\times F\text{,}\) en fonction de \(D_xf(u)\) et \(D_yf(u)\text{.}\)

Spoiler.

3. Etape 2.

Montrer que \(Dg(u_0)\) est un isomorphisme linéaire \(E\times F \rightarrow E\times G\)

  1. D'abord dans le cas \(E=\R^n,F=G=\R^p\text{;}\)

  2. Puis dans le cas général.

Spoiler.

4. Etape 3.

En déduire qu'il existe un voisinage \(V_1\) de \(x_0\) dans \(E\) et un voisinage \(W\) de \(y_0\) dans \(F\) tels que

  • \(g_{|V_1\times W}\) est un \(C^1\)-difféomorphisme sur son image

  • \(g(V_1\times W)\) est un ouvert de \(E\times G\) qui contient \((x_0,0_G)\)

Indice.

D'abord, appliquer le TIL à \(g\) en \(u_0\) puis adapter le résultat.

On rappelle à toutes fins utiles que \(E\times F\) est muni d'une des normes produit.

Spoiler.

5.

On pose

\begin{equation*} V=\{x\in E,(x,0_G)\in g(V_1\times W)\} \end{equation*}

Justifier que c'est un voisinage de \(x_0\) dans \(E\text{,}\) et montrer que, pour tout \(x\in V\text{,}\) il existe un unique élément de \(W\) tel que

\begin{equation*} g(x,y)=(x,0_G) \end{equation*}
Spoiler.

6.

On note \(\varphi(x)\) cet unique élément, ce qui définit une fonction \(\varphi:V \times W\text{.}\)

Justifier que \(\varphi\) fait le café, autrement dit vérifie:

  • \(\varphi\) est \(C^1\) sur \(V\text{;}\)

  • \begin{align*} (x,y)\in V\times W \amp \iff \amp x\in V\\ f(x,y)=0_G \amp \iff \amp y=\varphi(x)\\ \end{align*}

Spoiler.

7. Etape 4:.

Justifier que, pour tout \(u=(x,y)\in V_1 \times W\text{,}\) \(D_yf(u)\) est un isomorphisme linéaire.

Spoiler.

8.

Remarquer que, pour tout \(x\in V\text{,}\) on a

\begin{equation*} f(x,\varphi(x)) = 0_G \end{equation*}

et en déduire que, pour tout \(x\in V\) et pour tout \(h\in E\text{,}\)

\begin{equation*} D_xf(x,\varphi(x))(h) + (D_y f(x,\varphi(x)) \circ D\varphi(x) )(h) = 0_G. \end{equation*}
Indice.

Un coup de composée des différentielles et c'est plié !

On peut l'appliquer à \(f\circ \psi\) où \(\psi:x\in V\mapsto (x,\varphi(x))\text{.}\)

Ou alors, on peut calculer, pour \(h\in E\text{,}\)

\begin{equation*} f(x+h,\varphi(x+h)) \end{equation*}

en utilisant le fait qu'on sait déjà que \(\varphi\) est différentiable sur \(V\text{.}\)

Spoiler.