Section 2 L'espace vectoriel normé \(\mathcal L(E,F)\)
Notons \(\mathcal L(E,F)\) l'ensemble des applications linéaires continues de \(E\) dans \(F\text{.}\) Alors \(\mathcal L(E,F)\) est une espace vectoriel 1 .
De plus, si \(f\in \mathcal L(E,F)\text{,}\) on a vu qu'il existe \(C\gt0\) telle que, pour tout \(x\in E\text{,}\) \(\|f(x)\|_F \leq C\|x\|_E\text{.}\) On en déduit que le sous-ensemble:
est majoré (par \(C\)), et donc admet une borne supérieure. On peut donc définir une l'application suivante:
Définition 2.1.
On notera \(\|.\|_{\mathcal L(E,F)}\) l'application définie sur \(\mathcal L(E,F)\) par
et cette quantité est du plus haut intérêt:
Preuve guidée 2.1. Norme sur \(\mathcal L(E,F)\).
(a)
Montrer que
Montrons les deux égalités:
-
Soit \(x\in E\) tel que \(\|x\|_E=1\text{.}\) Alors \(x\neq 0_E\) donc
\begin{equation*} \|f(x)\|_F =\frac{\|f(x)\|_F}{\|x\|_E} \leq \sup_{x\neq 0_E}\frac{\|f(x)\|_F}{\|x\|_E}=\|f\|_{\mathcal L(E,F)} \end{equation*}donc \(\|f\|_{\mathcal L(E,F)}\) est un majorant de \(\{\|f(x)\|_F, \|x\|_E=1\}\text{,}\)et donc
\begin{equation*} \sup_{\|x\|_E=1}\|f(x)\|_F \geq \|f\|_{\mathcal L(E,F)} \end{equation*}D'unautre côté, soit \(y\neq 0_E\text{.}\) Posons \(x=\frac{y}{\|y\|_E}\text{;}\)alors \(\|x\|_E=1\) donc
\begin{equation*} \|f(x)\|_F\leq \sup_{\|x\|_E=1}\|f(x)\|_F \end{equation*}Or,
\begin{equation*} \|f(x)\|_F=\left\| \frac{y}{\|y\|_E}\right\|_F = \frac{\|f(y)\|_F}{\|y\|_E} \end{equation*}Donc, ona montré que \sup_{\|x\|_E=1}\|f(x)\|_F est un majorant de \(\left\{\frac{\|f(x)\|_F}{\|x\|_E}, x\in E\setminus \{0_E\}\right\}\text{,}\) donc
\begin{equation*} \|f\|_{\mathcal L(E,F)} \leq \sup_{\|x\|_E=1}\|f(x)\|_F \end{equation*} -
On a fait, à la Question 1.1.b, la remarque suivante: si \(C\) vérifie
\begin{equation*} \forall x\neq 0_E, \|f(x)\|_F \leq C\|x\|_E \end{equation*}alors cette inégalité est aussi vérifiée pour \(x=0_E\text{.}\) Donc:
\begin{align*} \{C\gt 0,\forall x\in E, \|f(x)\|_F \leq C\|x\|_E\}\amp =\{C\gt 0,\forall x\neq 0_E, \|f(x)\|_F \leq C\|x\|_E\}\\ \amp \left\{C\gt 0,\forall x\neq 0_E,\frac{\|f(x)\|_F}{\|x\|_E}\leq C\right\} \end{align*}Mais alors, \(\min \{C\gt 0,\forall x\in E, \|f(x)\|_F \leq C\|x\|_E\}\) est le plus petit majorant de \(\left\{\frac{\|f(x)\|_F}{\|x\|_E}, x\neq 0_E\right\}\text{,}\) et est donc bien égal à \(\sup_{x\neq 0_E}\frac{\|f(x)\|_F}{\|x\|_E} =\|f\|_{\mathcal L(E,F)}\text{.}\)
(b)
Une propriété pratique: montrer que pour tout \(x\in E\text{,}\)
Pour tout \(x\neq 0_E\text{,}\) on a
donc
et comme c'est vrai aussi pour \(x=0_E\text{,}\) on a gagné.
(c)
Montrer que \(\|.\|_{\mathcal L(E,F)}\) est une norme 2 sur \(\mathcal L(E,F)\text{.}\)
On a trois propriétés à démontrer. Allons-y gaiement:
-
Montrons que \(\|f\|_{\mathcal L(E,F)}=0\) ssi \(f=0_{\mathcal L(E,F)}\text{.}\)
\(\boxed{\Rightarrow}\) Supposons que \(\|f\|_{\mathcal L(E,F)}=0\text{.}\) Alors pour tout \(x\neq 0_E\text{,}\)
\begin{equation*} 0\leq \frac{\|f(x)\|_F}{\|x\|_E}\leq 0 \end{equation*}donc \(\|f(x)\|_F=0\text{,}\) donc \(f(x)=0_F\) pour tout \(x\neq 0_E\text{.}\) Comme c'est vrai aussi pour \(x=0_E\text{,}\) on a bien \(f=0_{\mathcal L(E,F)}\text{.}\)
\(\boxed{\Leftarrow}\) Si \(f=0_{\mathcal L(E,F)}\) alors, pour tout \(x\) de norme 1, on a \(f(x)=0_F\) donc \(\|f(x)\|_F=0\text{.}\) On en déduit que
\begin{equation*} \|f\|_{\mathcal L(E,F)}=\sup_{\|x\|_E=1}\|f(x)\|_F = \sup \{ 0 \} =0 \end{equation*} -
Montrons que, pour tous \(\lambda\in \R\text{,}\) \(f\in \mathcal L(E,F)\text{,}\)
\begin{equation*} \|\lambda f\|_{\mathcal L(E,F)} = |\lambda|\|f\|_{\mathcal L(E,F)} \end{equation*}Soient donc \(\lambda\in \R\text{,}\) \(f\in \mathcal L(E,F)\) .D'un côté, on a, pour tout \(x\in E\text{,}\)
\begin{equation*} \|\lambda f(x)\|_F = |\lambda| \|f(x)\|_F \leq |\lambda| \|f\|_{\mathcal L(E,F)} \|x\|_E \end{equation*}Donc \(|\lambda| \|f\|_{\mathcal L(E,F)} \in \{C\gt 0,\forall x\in E, \|f(x)\|_F \leq C\|x\|_E\}\text{,}\) donc, d'après la deuxième égalité de la Question 2.1.a,
\begin{equation*} \|\lambda f\|_{\mathcal L(E,F)} \leq |\lambda|\|f\|_{\mathcal L(E,F)} \end{equation*}\(\leadsto\) Jusqu'ici, on a donc obtenu, pour tout \(g\in \mathcal L(E,F)\text{,}\) pour tout \(\mu\in\R\text{,}\)
\begin{equation*} (\star)\quad \|\mu g\|_{\mathcal L(E,F)} \leq |\mu|\|g\|_{\mathcal L(E,F)} \end{equation*}Reste à montrer que \(\|\lambda f\|_{\mathcal L(E,F)} \geq |\lambda|\|f\|_{\mathcal L(E,F)}\text{.}\)
Si \(\lambda =0\text{,}\) d'après (1), ça marche.
Si \(\lambda \neq 0\text{,}\)
\begin{align*} \|f\|_{\mathcal L(E,F)} \amp= \left\|\frac1{\lambda} \lambda f\right\|_{\mathcal L(E,F)}\\ \amp \leq \frac1{|\lambda|}\|\lambda f\|_{\mathcal L(E,F)} \text{ d'après }(\star) \end{align*}où on applique \((\star)\) avec \(g=\lambda f\) et \(\mu = \frac1{\lambda}\text{.}\) On trouve donc
\begin{equation*} |\lambda|\|f\|_{\mathcal L(E,F)}\leq \|\lambda f\|_{\mathcal L(E,F)} \end{equation*}comme souhaité.
-
Montrons que pour tous \(f,g\in \mathcal L(E,F)\text{,}\)
\begin{equation*} \|f+g\|_{\mathcal L(E,F)}\leq\|f\|_{\mathcal L(E,F)}+\|g\|_{\mathcal L(E,F)} \end{equation*}Soient donc \(f,g\in \mathcal L(E,F)\text{.}\) Alors pour tout \(x\in E\) de norme 1,
\begin{equation*} \|f(x)+g(x)\|_F \leq \|f(x)\|_F+\|g(x)\|_F \leq \|f\|_{\mathcal L(E,F)} + \|g\|_{\mathcal L(E,F)} \end{equation*}donc \(\|f\|_{\mathcal L(E,F)} + \|g\|_{\mathcal L(E,F)}\) majore l'ensemble \(\{\|f(x)+g(x)\|_F,\|x\|_E=1\}\text{,}\) donc, d'après la première égalité de la Question 2.1.a,
\begin{equation*} \|f+g\|_{\mathcal L(E,F)}\leq\|f\|_{\mathcal L(E,F)}+\|g\|_{\mathcal L(E,F)} \end{equation*}
Une illustration de ce que calcule cette norme:
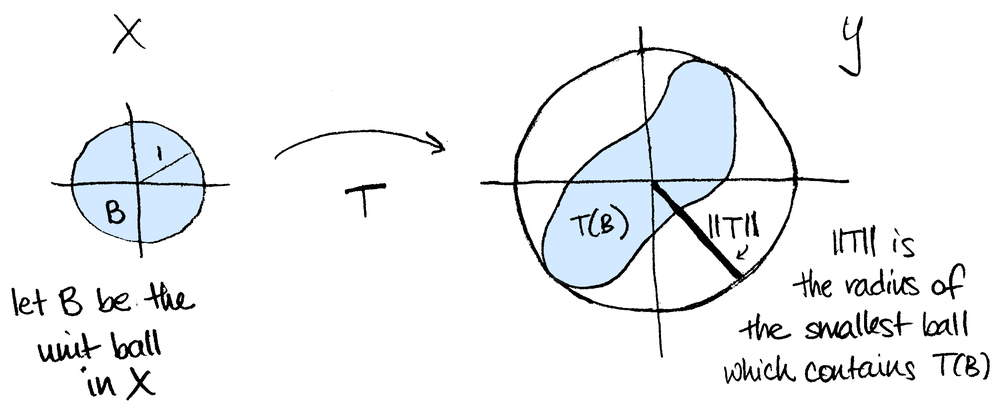
https://www.math3ma.com/blog/operator-norm-intuitivelyExercice 2.3. Un exemple de calcul de norme d'application linéaire.
Reprenons l'application définie à l'Exercice 1.1 sur \((E=\mathcal C^0([0,1],\R),\|.\|_\infty)\) par:
Montrer que l'application \(A\in \mathcal L(E,\R)\) est de norme 1.
Le calcul fait à l'Exercice 1.1 pour montrer que \(A\) est continue justifie que \(\|A\|_{\mathcal L(E,\R)}\leq 1\text{.}\) Reste à montrer l'autre inégalité. Pour cela, on peut utiliser le fait que
Puisque le sup est un majorant, il suffit de trouver une fonction (simple !) \(f\in E\) telle que \(\|f\|_\infty= 1\) et \(|A(f)|=1\text{.}\)
Comme remarqué dans l'indice, il nous reste à montrer que
Pour ça, considérons la fonction constante égale à 1: \(f_1:x\in[0,1]\mapsto 1\text{.}\) Alors \(f_1\in E\text{,}\) et on a \(\|f_1\|_\infty = 1\text{.}\) De plus
donc on a bien \(\|A\|_{\mathcal L(E,\R)}\geq 1\text{.}\)
Une remarque importante: La norme \(\|.\|_{\mathcal L(E,F)}\) dépend à la fois des normes choisies sur \(E\) et \(F\text{:}\) si on change de normes sur les e.v. \(E,F\text{,}\) la norme \(\|.\|_{\mathcal L(E,F)}\) sur \(\mathcal L(E,F)\) change aussi.
Pour appuyer là-dessus, on dit parfois que \(\|.\|_{\mathcal L(E,F)}\) est la norme d'application linéaire induite par les normes \(\|.\|_E\) sur \(E\) et \(\|.\|_F\) sur \(F\text{.}\)
Illustrons ce point sur \(\R^n\text{,}\) où on peut faire des calculs explicites:
Preuve guidée 2.2. Norme induite par la norme 1.
Soit \(f:\R^n \rightarrow \R^p\) une application linéaire. Alors \(f\) est représentée par sa matrice dans les bases canoniques \(A=(a_{ij}) \in \mathcal M_{p,n}(\R)\text{.}\)
On munit \(\R^n\) et \(\R^p\) de la norme \(\|.\|_1\text{.}\) On va montrer que la norme d'application linéaire induite sur \(\mathcal L(\R^n,\R^p)\) est donnée par
Essayer de calculer ce truc pour quelques matrices \(2\times 2\text{,}\) pour se faire une idée.
(a)
Comme souvent, on va procéder par double inégalité. Posons, pour se simplifier la vie,
Montrer que pour tout \(x\in \R^n\text{,}\)
ce qui nous donne \(\|f\|_{\mathcal L,1}\leq M\text{.}\)
Soit donc \(x\in \R^n\text{.}\) Calculons
comme on voulait.
(b)
Reste à montrer que \(\|f\|_{\mathcal L,1}\geq M\text{.}\)
Il vous faut juste un vecteur \(x\) de norme 3 1 tel que \(\|f(x)\|_1=M.\)

Allez-y !
Soit \(j_0\in\{1,\ldots,n\}\) tel que \(M=\sum_{i=1}^p |a_{ij_0}|\text{.}\) Essayer de calculer \(\|f(e_{j_0})\|_1\text{,}\) où \(e_{j_0}\) est le \(j_0\)-ème vecteur de labase canonique.
Soit \(e_{j_0}=(0,...,1,0,...0)\) le \(j_0\)-ème vecteur de la base canonique. Par définition de \(A\text{,}\) \(f(e_{j_0})\) est la \(j_0\)-ème colonne de \(A\) donc
Puisque \(\|e_{j_0}\|_1=1\text{,}\) on en déduit, par la première égalité de la Question 2.1.a, que \(\|f\|_{\mathcal L,1}\geq M\text{.}\)
Preuve guidée 2.3. Norme induite par la norme \(\infty\).
Soit \(f:\R^n \rightarrow \R^p\) une application linéaire et \(A=(a_{ij}) \in \mathcal M_{p,n}(\R)\) sa matrice dans les bases canoniques.
On munit \(\R^n\) et \(\R^p\) de la norme \(\|.\|_\infty\text{.}\) On va montrer que la norme d'application linéaire induite sur \(\mathcal L(\R^n,\R^p)\) est donnée par
(a)
Comme on ne change pas une équipe qui gagne, on va montrer deux inégalités. Posons, cette fois,
Calculer, pour tout \(x\in \R^n\text{,}\)
et majorer par \(M'\|x\|_\infty\text{,}\) ce qui nous donne \(\|f\|_{\mathcal L,\infty}\leq M'\text{.}\)
Soit donc \(x\in \R^n\text{.}\) Calculons
comme on voulait.
(b)
Reste à montrer que \(\|f\|_{\mathcal L,1}\geq M'\text{.}\)
Il vous faut un vecteur \(x\) de norme 4 1 tel que \(\|f(x)\|_1=M.\)

Allez-y !
Si on suppose tous les \(a_{ij}\) positifs, et qu'on prend \(v_0=(1,1,...1)\in \R^n\text{,}\) que donne \(\|f(v_0)\|_\infty\) ? Et s'ils n'étaient pas tous positifs, que faudrait-il changer ?
Soit \(i_0\in\{1,\ldots,p\}\) tel que \(M'=\sum_{j=n}^p |a_{i_0j}|\text{.}\) Pour garder avoir des égalités dans le calcul précédent, on veut "rendre positifs" les éventuels \(a_{i_0j}\) négatifs. On pose, pour chaque \(j\text{,}\)
Du coup,
et on a, pour tout \(i\text{,}\)
Du coup, pour \(v_0=(sgn(a_{i_01}),sgn(a_{i_02}),...sgn(a_{i_0n}))\in \R^n\text{,}\) le calcul précédent donne
Puisque \(\|v_0\|_\infty=1\text{,}\) on en déduit, par la première égalité de la Question 2.1.a, que \(\|f\|_{\mathcal L,\infty}\geq M'\text{.}\)
Preuve guidée 2.4. Norme induite par la norme 2.
Soit \(f:\R^n \rightarrow \R^p\) une application linéaire et \(A=(a_{ij}) \in \mathcal M_{p,n}(\R)\) sa matrice dans les bases canoniques.
De plus, pour toute matrice carrée \(B\in \mathcal M_n(\R)\text{,}\) on note \(\rho(B)\) son rayon spectral:
On munit \(\R^n\) et \(\R^p\) de la norme euclidienne \(\|.\|_2\text{.}\) On va montrer que la norme d'application linéaire induite sur \(\mathcal L(\R^n,\R^p)\) est donnée par
(a)
Soit \(x\in\R^n\text{.}\) Commençons, comme toujours, par majorer \(\|f(x)\|_2\text{.}\)
Montrer que \(\|f(x)\|_2^2=\langle {}^tAA x,x \rangle\text{,}\) où \(\langle.,.\rangle\) est le produit scalaire usuel sur \(\R^n\text{.}\)
Et on calcule:
par définition de la matrice transposée.
(b)
Montrer que la matrice \({}^tAA\in \mathcal M_n(\R)\) admet \(n\) valeurs propres positives 5
et qu'elle est diagonalisable dans une base orthonormée \((v_1,\ldots,v_n)\text{.}\)
On rappelle ce précieux résultat d'algèbre linéaire:
Théorème 2.4. Réduction des endomorphismes symétriques.
Soit \(M\) une matrice symétrique réelle. Alors il existe une base orthonormée constituée de vecteurs propres de \(M\text{.}\)
Montrons que la matrice \({}^tAA\) est symétrique. On a :
donc, d'après le théorème de réduction des matrices symétriques, il existe une b.o.n. \((v_1,\ldots,v_n)\) de vecteurs propres de \({}^tAA\text{:}\) quitte à la ranger un peu mieux, on peut supposer que les valeurs propres associées \(\lambda_1,...,\lambda_n\) (éventuellement comptées plusieurs fois, s'il y a des valeurs propres à multiplicité) sont dans l'ordre:
Reste à montrer que ces valeurs propres sont positives. Or on a, pour tout \(i=1...n\text{,}\)
donc
Or \(v_i\) est de norme 1, donc
et on a vu plus haut que
donc on a bien \(\lambda_i\geq 0\text{.}\)
(c)
Pour un \(x\in\R^n\) quelconque, écrire \(x\) dans la base \((v_1,\ldots,v_n)\text{.}\)
En déduire que
et donc, que
Chef oui chef, posons donc \(x=x_1v_1+...+x_nv_n\text{,}\) alors d'après le calcul fait plus haut,
et comme \(0\leq\max_i \lambda_i=\rho({}^tAA)\text{,}\) on a bien obtenu que pour tout \(x\in\R^n\text{,}\)
d'où \(\|f\|_{\mathcal L,2} \leq \sqrt{\rho({}^tA A)}\text{.}\)
(d)
Dans cette b.o.n. \((v_1,\ldots,v_n)\text{,}\) ne peut-on pas trouver un vecteur \(v_{i_0}\) de norme 1 tel que
Si par hasard c'était le cas, conclure.
Soit \(i_0\) tel que \(\rho({}^tAA)=\max_i \lambda_i= \lambda_{i_0}\text{.}\) Alors \(\|v_{i_0}\|_2=1\) et
donc
et puisque
on a bien obtenu l'inégalité qui nous manquait.
Ainsi, muni de \(\|.\|_{\mathcal L(E,F)}\text{,}\) \(\mathcal L(E,F)\) devient un espace vectoriel normé: on peut donc parler de ses ouverts, de ses suites, de ses compacts, bref, on peut utiliser tout l'arsenal des e.v.n.

En particulier, on a la propriété topologique suivante:
Proposition 2.5.
Si \((F,\|.\|_F)\) est complet, alors \((\mathcal L(E,F),\|.\|_{\mathcal L(E,F)})\) est également complet.
Or, dans un espace vectoriel normé complet (aussi appelé espace de Banach), on sait que, non seulement les suites de Cauchy convergent, mais on a aussi un résultat sur les séries:
Proposition 2.6.
Soit \((E,\|.\|_E)\) un espace de Banach, et soit \((u_n)_{n\in\N}\in E^\N\) une suite de \(E\text{.}\)
On suppose que la série de terme général \((u_n)_{n\in\N}\) converge normalement, c'est à dire que la série réelle de terme général \((\|u_n\|)_n\) converge:
Alors la série de terme général \((u_n)_{n\in\N}\) est convergente 6 .
Donc, si \((F,\|.\|_F)\) est complet, alors, pour toute suite d'applications linéaires continues \((A_n)_n\in \mathcal L(E,F)^\N\)telle que la série réelle \(\sum \|A_n\|_{\mathcal L(E,F)}\) converge, la suite d'applications linéaires \((S_n=\sum_{k=0}^n A_k)_n\) converge dans \(\mathcal L(E,F)\text{,}\) et on peut donc définir l'application linéaire \(S=\sum_{k=0}^\infty A_k\text{.}\)
De plus, la norme induite bénéficie de quelques agréables propriétés calculatoires:
Proposition 2.7.
- \(\|id_E\|_{\mathcal L(E)}=1\text{.}\)
- Pour tous \(f\in\mathcal L(E,F),g\in\mathcal L(F,G)\text{,}\) on a \(\|g\circ f\|_{\mathcal L(E,G)} \leq \|g\|_{\mathcal L(F,G)} \|f\|_{\mathcal L(E,F)}\text{.}\)
-
Pour tout \(f\in\mathcal L(E)\text{,}\) pour tout \(n\in\N\text{,}\)
\begin{equation*} \|f^n \|_{\mathcal L(E)} = \|\underbrace{f\circ ...\circ f}_{n\text{ fois}}\|_{\mathcal L(E)} \leq \|f\|^n _{\mathcal L(E)} \end{equation*}
Remarque 2.8.
Le troisième point est particulièrement utile pour étudier la convergence de séries de terme général du type \(u_n=T^n\) pour \(T\in\mathcal L(E)\text{,}\) puisqu'il permet de comparer à des séries réelles géométriques, qui ne sont pas les plus méchantes.