Compléments sur les suites et séries

Sous-section 3.1 La preuve d'Euler

On va ici utiliser l'approche utilisée par Euler en 1735 pour démontrer l'égalité \(\sum_n \frac1{n^2} = \frac{\pi^2}{6}\text{,}\) en s'appuyant sur l'excellente vidéo de Mathologer^1  2

Attention: Cette preuve date de 1735 et n'est pas rigoureuse! Elle a été rendue "propre" par Weierstrass un siècle plus tard, en utilisant de l'analyse complexe³. L'idée est donc surtout de donner une idée de comment ça marche, mais ne faites pas ça sans guide compétent et certifié !

Exercice 3.1. \(\sin(x)\) vu comme un polynôme.

Pour faire sortir le \(\pi\) qu'il nous faut, on se tourne vers la fonction \(\sin\text{.}\) Et, brièvement, on va imaginer que \(\sin\) est une sorte de "polynôme infini".

Kwa ?

En fait, ce n'est pas si délirant si on considère cette formule que vous connaissez déjà:

\begin{equation*} \sin(x)= x - \frac{x^3}{3!}+ \frac{x^5}{5!} -... \end{equation*}

Plus tard dans l'année, on va étudier les séries entières, et on apprendra que pour tout \(x\in\mathbb R\) on peut écrire rigoureusement

\begin{equation*} \sin(x)= \sum_{n=0}^{+\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!} \end{equation*}

Donc cette idée de "polynôme infini" est dangereuse, mais pas totalement aberrante.

(a)

Déterminer les \(x\in \mathbb R\) tels que \(\sin(x)=0\text{.}\)

Spoiler.

\begin{equation*} \sin(x)=0 \iff x=k\pi,\ k\in \mathbb Z. \end{equation*}

(b)

Toujours en imaginant que \(\sin\) est en fait un polynôme, en déduire qu'il existe une constante \(\alpha \in \mathbb R\) telle que

\begin{equation*} \sin(x)= \alpha x (1-\frac{x^2}{\pi^2})(1-\frac{x^2}{4\pi^2})(1-\frac{x^2}{9\pi^2})... \end{equation*}

Indice 1.

Si \(P\) est un polynôme et \(x_0\) est une racine de \(P\text{,}\) par quoi peut-on factoriser \(P\text{?}\)

Indice 2.

\begin{equation*} x-x_0 = -x_0(1-\frac x{x_0}) \end{equation*}

Spoiler.

D'après la question précédente, pour tout \(k\in \mathbb Z\text{,}\) \(k\pi\) est une racine de \(\sin(x)\text{.}\) Si \(\sin(x)\) est un polynôme, on peut donc le factoriser par \((x-k\pi) = -k\pi(1-\frac{x}{k\pi})\) pour tout \(k\in \mathbb Z\text{,}\) ce qui donne:

\begin{equation*} \sin(x)=\alpha (x-0)\left(1-\frac{x}{\pi}\right)\left(1+\frac{x}{k\pi}\right)\left(1-\frac{x}{2\pi}\right)\left(1+\frac{x}{2\pi}\right).... \end{equation*}

Or, pour tout \(k\in\mathbb{N}^*\text{,}\) \(\left(1-\frac{x}{k\pi}\right)\left(1+\frac{x}{k\pi}\right)=\left(1-\frac{x^2}{k^2\pi^2}\right)\text{,}\) d'où la formule souhaitée

\begin{equation*} \sin(x)= \alpha x \left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\left(1-\frac{x^2}{9\pi^2}\right)... \end{equation*}

(c)

Calculer \(\lim_{x\rightarrow 0}\frac{\sin(x)}{x}.\) En déduire que \(\alpha =1\text{.}\)

Indice.

\(\frac{\sin(x)}{x}=\frac{\sin(x)-\sin(0)}{x-0}.\)

Spoiler.

On peut réécrire \(\frac{\sin(x)}{x}\) comme le taux d'accroissement de la fonction \(\sin\) en 0, ce qui donne

\begin{equation*} \lim_{x\rightarrow 0}\frac{\sin(x)}{x}=\lim_{x\rightarrow 0}\frac{\sin(x)-\sin(0)}{x-0}= \sin'(0)=\cos(0)=1. \end{equation*}

or on a obtenu

\begin{align*} \frac{\sin(x)}{x}\amp = \alpha (1-\frac{x^2}{\pi^2})(1-\frac{x^2}{4\pi^2})(1-\frac{x^2}{9\pi^2})...\\ \amp \xrightarrow[]{x\rightarrow 0} \alpha \end{align*}

Donc, par unicité de la limite, \(\alpha=1\) et

\begin{equation*} \frac{\sin(x)}{x} = (1-\frac{x^2}{\pi^2})(1-\frac{x^2}{4\pi^2})(1-\frac{x^2}{9\pi^2})... \end{equation*}

(d)

On va maintenant développer le polynôme⁴. On a donc trouvé que \(\frac{\sin(x)}{x}\) est un polynôme en \(x^2\text{:}\)

\begin{equation*} \frac{\sin(x)}{x} = \left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\left(1-\frac{x^2}{9\pi^2}\right)... \end{equation*}

Il existe donc \(A_2,A_4,...\) tels que

\begin{equation*} \frac{\sin(x)}{x} = A_0+ A_2 x^2 + A_4 x^4 +.... \end{equation*}

Déterminer \(A_0\) et \(A_2\text{.}\)

Spoiler.

Lorsqu'on développe le produit \(\left(1-\frac{x^2}{\pi^2}\right)\left(1-\frac{x^2}{4\pi^2}\right)\left(1-\frac{x^2}{9\pi^2}\right)\text{,}\) on va obtenir tous les produits possibles de \(1\) et \(-\frac{x^2}{k^2\pi^2}\) pour \(k\) allant de 1 à \(+\infty\text{.}\)

La seule façon d'avoir un terme constant est donc de prendre le 1 dans chaque parenthèse, ce qui donne \(A_0=1*1*1...=1\text{.}\)

D'un autre côté, les termes en \(x^2\) vont être ceux obtenus en prenant un seul des termes \(\frac{x^2}{k^2\pi^2}\text{,}\) multiplié par le 1 de tous les autres facteurs (sinon on se retrouve avec un terme en \(x^4\) au moins). Au total, tous ces termes donnent

\begin{equation*} -\frac{x^2}{\pi^2}-\frac{x^2}{4\pi^2}-\frac{x^2}{9\pi^2}-...=-\left(\frac1{\pi^2}+\frac1{4\pi^2}+...\right)x^2 \end{equation*}

D'où finalement

\begin{align*} A_2\amp=-\left(\frac1{\pi^2}+\frac1{4\pi^2}+...\right)\\ \amp =-\frac1{\pi^2}\left(1+\frac14+\frac19...\right)\\ \amp =-\frac1{\pi^2}\sum_{k=1}^\infty \frac1{k^2} \end{align*}

(e)

En utilisant le développement limité de \(\sin\) en 0, montrer que

\begin{equation*} \frac{\sin(x)}{x} = 1- \frac{x^2}{3!} + \frac{x^4}{5!}+... \end{equation*}

En déduire que \(A_2=-\frac16\text{.}\) Conclure.

Spoiler.

On sait que pour un polynôme \(P\in\mathbb{R}[X]\text{,}\) si on a

\begin{equation*} P=a_0+a_1X+...+a_nX^n = b_0+b_1X+...+b_nX^n \end{equation*}

alors on peut identifier les coefficients: \(a_i=b_i\) pour tout \(i\in\{1,\ldots n\}\text{.}\)

On va dire que ça marche aussi pour les polynômes infinis. Or on a le développement de Taylor de \(\sin:\)

\begin{equation*} \sin(x) = x- \frac{x^3}{3!}+ \frac{x^5}{5!}+... \end{equation*}

donc⁵

\begin{equation*} \frac{\sin(x)}{x} = 1 - \frac{x^2}{3!}+ \frac{x^4}{5!}+... \end{equation*}

Et d'un autre côté on a trouvé

\begin{equation*} \frac{\sin(x)}{x}=1-\frac1{\pi^2}\left(\sum_{k=1}^\infty \frac1{k^2}\right)x^2+... \end{equation*}

Donc, en identifiant les coefficients correspondant à \(x^2\text{:}\)

\begin{equation*} -\frac1{\pi^2}\left(\sum_{k=1}^\infty \frac1{k^2}\right)=- \frac{1}{3!} \end{equation*}

Autrement dit,

\begin{equation*} \sum_{k=1}^\infty \frac1{k^2}= \frac{\pi^2}{6}. \end{equation*}

Sous-section 3.2 Une version un chouïa plus rigoureuse

Exercice 3.2.

On va à nouveau écrire \(\sin\) comme un produit infini. Cette histoire est plus sérieuse qu'elle n'en a l'air: l'écriture de certaines fonctions, dites "entières"⁶, sous forme de produit infini, est un résultat d'analyse dans les complexes. On l'appelle le théorème de factorisation de Weierstrass⁷, et il donne en particulier, pour tout \(x\in ]0,\frac12[\text{,}\)

\begin{equation} \frac{\sin(\pi x)}{\pi x}=\prod_{n=1}^\infty \left(1-\frac{x^2}{n^2}\right)\tag{3.1} \end{equation}

Les produits infinis s'étudient comme les séries: on étudie la suite \((P_n)_n\) définie par le produit \(\prod_{k=1}^n a_k\text{.}\) Si \((P_n)_n\) a une limite quand \(n\rightarrow \infty\text{,}\) on note cette limite \(\prod_{k=1}^\infty a_k\text{.}\)

(a)

En général, pour étudier un tel produit, on prend le logarithme de façon à se ramener à une somme.

\(\leadsto\) Qu'obtient-on quand on prend le logarithme de l'égalité (3.1) ?

Spoiler.

On trouve

\begin{equation} \ln(\sin(\pi x))-\ln(\pi x)= \sum_{n=1}^\infty \ln\left(1-\frac{x^2}{n^2}\right).\tag{3.2} \end{equation}

(b)

En prenant la dérivée de l'expression obtenue, montrer que, pour tout \(x\in ]0,\frac12[\)

\begin{equation} \frac1{2x^2} - \frac{\pi \cos(\pi x)}{2x\sin(\pi x)}= \sum_{n=1}^\infty \frac{1}{n^2-x^2}\tag{3.3} \end{equation}

Spoiler.

En utilisant le fait que \((\ln\circ f)' = \frac{f'}{f}\text{,}\) si on dérive l'expression obtenue à la question précédente, on trouve, pour le terme de gauche:

\begin{equation*} \frac{\pi \cos(\pi x)}{\sin(\pi x)} - \frac{\pi}{\pi x} \end{equation*}

Pour le terme de droite, remarquons que la série de fonctions \(\sum \ln\left(1-\frac{x^2}{n^2}\right)\) converge normalement⁸: en effet, pour tout \(x\in ]0,\frac12[\text{,}\)

\begin{equation*} \left|\ln\left(1-\frac{x^2}{n^2}\right)\right| = -\ln\left(1-\frac{x^2}{n^2}\right) \leq -\ln\left(1-\frac1{4n^2}\right) \end{equation*}

et \(-\ln\left(1-\frac1{4n^2}\right)\simeq \frac{1}{4n^2}\) est le terme général d'une série convergente. On peut donc bien dériver la somme du membre de droite de (3.2) terme à terme, ce qui donne

\begin{equation*} \sum_{n=1}^\infty \frac{-\frac{2x}{n^2}}{\frac{n^2-x^2}{n^2}} \end{equation*}

D'où, au total,

\begin{equation*} \frac{\pi \cos(\pi x)}{\sin(\pi x)} - \frac{1}{ x} =\sum_{n=1}^\infty \frac{-2x}{n^2-x^2} \end{equation*}

et de là, on obtient (3.3) en divisant par \(-2x\text{.}\)

(c)

Ici, on va s'occuper du terme \(\frac{\cos(\pi x)}{\sin(\pi x)}\text{.}\) En utilisant les formules d'Euler⁹, montrer que

\begin{equation*} \frac{\cos(\pi x)}{\sin(\pi x)} = i\left(1+\frac{2}{e^{2i\pi x} -1}\right) \end{equation*}

Indice.

On peut remarquer que \(e^{ia}+e^{-ia}=e^{-ia}(e^{2ia}+1)\text{,}\) ce qui permet de simplifier une partie des exponentielles.

Spoiler.

Les formules d'Euler nous donnent

\begin{equation*} \cos(\pi x) = \frac{e^{i\pi x}+e^{-i\pi x}}2,\ \sin(\pi x)=\frac{e^{i\pi x}-e^{-i\pi x}}{2i} \end{equation*}

donc

\begin{align*} \frac{\cos(\pi x)}{\sin(\pi x)} \amp= i\frac{e^{i\pi x}+e^{-i\pi x}}{e^{i\pi x}-e^{-i\pi x}}\\ \amp = i\frac{e^{-i\pi x}(e^{i2\pi x}+1)}{e^{-i\pi x}(e^{i2\pi x}-1)}\\ \amp = i\frac{e^{i2\pi x}-1+2}{e^{i2\pi x}-1}\\ \amp= i\left(1+\frac{2}{e^{2i\pi x} -1}\right), \end{align*}

comme souhaité.

(d)

On a donc obtenu:

\begin{equation*} \frac1{2x^2} - \frac{i\pi}{2x}\left(1+\frac{2}{e^{2i\pi x} -1}\right) = \sum_{n=1}^\infty \frac{1}{n^2-x^2} \end{equation*}

ce qui pourrait nous mettre de mauvaise humeur, car maintenant, on a des complexes partout. On va s'en débarrasser en appliquant la formule à \(x=-it\)¹⁰. Montrer que ça donne

\begin{equation*} \frac{1-e^{2\pi t}+\pi t e^{2\pi t} + \pi t}{2(t^2e^{2\pi t}-t^2)} = \sum_{n=1}^\infty \frac{1}{n^2+t^2} \end{equation*}

Spoiler.

Remplaçons tous les \(x\) par \(-it\text{,}\) et donc les \(x^2\) deviennent des \(-t^2\text{.}\) On se retrouve avec

\begin{equation*} -\frac1{2t^2} + \frac{\pi}{2t}\left(1+\frac{2}{e^{2\pi t} -1}\right) = \sum_{n=1}^\infty \frac{1}{n^2+t^2} \end{equation*}

c'est-à-dire

\begin{equation*} -\frac1{2t^2} + \frac{\pi}{2t}+\frac{2\pi}{2t(e^{2\pi t} -1)} = \sum_{n=1}^\infty \frac{1}{n^2+t^2} \end{equation*}

Reste à mettre les trois fractions du membre de gauche sur le même dénominateur:

\begin{equation*} -\frac{e^{2\pi t} -1}{2t^2(e^{2\pi t} -1)} +\frac{\pi t(e^{2\pi t} -1)}{2t^2(e^{2\pi t} -1)}+\frac{2\pi t}{2t^2(e^{2\pi t} -1)} = \sum_{n=1}^\infty \frac{1}{n^2+t^2} \end{equation*}

ce qui donne

\begin{equation*} \frac{1-e^{2\pi t} + \pi t e^{2\pi t} - \pi t +2\pi t}{2t^2(e^{2\pi t} -1)} = \sum_{n=1}^\infty \frac{1}{n^2+t^2}. \end{equation*}

(e)

Maintenant, on aimerait prendre la limite quand \(t\rightarrow 0\text{.}\) Le terme de droite donne alors notre somme mystérieuse \(\sum_{n=1}^\infty \frac{1}{n^2}\text{.}\)

Par contre, le terme de droite donne une indétermination \(\frac00\text{.}\) Pour s'en débarasser, appliquez trois fois¹¹ la règle de l'Hôpital¹²: ça devrait donner

\begin{align*} \lim_{t\rightarrow 0} \frac{1-e^{2\pi t}+\pi(te^{2\pi t} + t)}{2(t^2e^{2\pi t}-t^2)}\amp =\lim_{t\to 0}\frac {\pi ^{2}(2\pi t+1)}{4\pi ^{2}t^{2}+12\pi t+6}\\ \amp = \frac{\pi^2}6 \end{align*}

Spoiler.

Commençons par dériver le numérateur:

\begin{align*} (1-e^{2\pi t}+\pi t e^{2\pi t} + \pi t)' \amp =-2\pi e^{2\pi t} + \pi e^{2\pi t} + 2\pi^2 t e^{2^pi t} + \pi\\ \amp=- \pi e^{2\pi t} + 2\pi^2 t e^{2^pi t} + \pi \end{align*}

Le dénominateur donne:

\begin{equation*} (2(t^2e^{2\pi t}-t^2))'= 4(te^{2\pi t}+ \pi t^2e^{2\pi t} -t) \end{equation*}

et la règle de l'Hôpital nous dit que

\begin{equation*} \lim_{t\rightarrow 0} \frac{1-e^{2\pi t}+\pi(te^{2\pi t} + t)}{2(t^2e^{2\pi t}-t^2)} = \lim_{t\rightarrow 0}\frac{- \pi e^{2\pi t} + 2\pi^2 t e^{2^pi t} + \pi}{4(te^{2\pi t}+ \pi t^2e^{2\pi t} -t)} \end{equation*}

ce qui...est encore une forme indéterminée. On retrousse les manches et on renvoie la fraction de droite à l'Hôpital:

\begin{align*} (- \pi e^{2\pi t} + 2\pi^2 t e^{2^pi t} + \pi)'\amp =-2\pi^2 e^{2^pi t}+2\pi^2 e^{2^pi t}+4\pi^3 t e^{2^pi t}\\ \amp = 4\pi^3 t e^{2^pi t} \end{align*}

et d'autre part

\begin{align*} 4(te^{2\pi t}+ \pi t^2e^{2\pi t} -t)'\amp= 4 (e^{2\pi t}+2\pi t e^{2\pi t}+ 2\pi te^{2\pi t}+2\pi^2t^2 e^{2\pi t}-1)\\ \amp=4((2\pi^2 t^2 + 4 \pi t + 1)e^{2\pi t}-1) \end{align*}

d'où, par l'Hôpital,

\begin{equation*} \lim_{t\rightarrow 0}\frac{- \pi e^{2\pi t} + 2\pi^2 t e^{2^pi t} + \pi}{4(te^{2\pi t}+ \pi t^2e^{2\pi t} -t)}= \lim_{t\rightarrow 0}\frac{ 4\pi^3 t e^{2^pi t}}{4((2\pi^2 t^2 + 4 \pi t + 1)e^{2\pi t}-1)} \end{equation*}

ce qui est... encore indéterminé, on ne s'énerve pas, on continue:

\begin{align*} (4\pi^3 t e^{2^pi t})'\amp=4\pi^3 e^{2^pi t} + 8\pi^4 t e^{2^pi t}\\ \amp = 4\pi^3(1+2\pi t)e^{2^pi t} \end{align*}

et, d'autre part

\begin{align*} (4((2\pi^2 t^2 + 4 \pi t + 1)e^{2\pi t}-1))'\amp= 8\pi(2\pi^2 t^2 + 4 \pi t + 1)e^{2\pi t}+4(4\pi+4\pi^2t)e^{2\pi t}\\ \amp= 4\pi(4\pi^2 t^2+ 8\pi t+2+4+4\pi t)e^{2\pi t}\\ \amp=4\pi(4\pi^2 t^2+8\pi t + 2 + 4 +4 \pi t)e^{2\pi t}\\ \amp=4\pi(4\pi^2 t^2 + 12 \pi t + 6)e^{2\pi t} \end{align*}

donc, par la règle de l'Hôpital

\begin{align*} \lim_{t\rightarrow 0}\frac{ 4\pi^3 t e^{2^pi t}}{4((2\pi^2 t^2 + 4 \pi t + 1)e^{2\pi t}-1)}\amp = \lim_{t\rightarrow 0} \frac{4\pi^3(1+2\pi t)e^{2^pi t}}{4\pi(4\pi^2 t^2 + 12 \pi t + 6)e^{2\pi t}}\\ \amp = \lim_{t\rightarrow 0} \frac{\pi^2(1+2\pi t)}{4\pi^2 t^2 + 12 \pi t + 6}\\ \amp = \frac{\pi^2}6 \end{align*}

Sous-section 3.3 Une preuve "géométrique"

On va ici donner une preuve complètement différente, mais plus jolie, du résultat \(\sum_{n=1}^\infty \frac1{n^2} = \frac{\pi^2}6\text{,}\) qui consiste à donner une reformulation géométrique du problème.

Cette reformulation géométrique fait intervenir un cercle, et c'est de là que \(\pi\) va sortir.

La preuve est dûe à J. Wästlund de l'université Chalmers, et est disponible en entier ici¹³. Une très belle illustration vidéo a été réalisée par Grant Sanderson, de l'excellente chaîne YouTube 3blue1brown:

Pour montrer que

on va montrer, plus généralement, que pour tout \(x\in ]0,\frac12]\text{,}\)

Pour cela, on va regarder les étoiles.

Si on observe une étoile située à distance \(d\text{,}\) l'intensité lumineuse que l'on reçoit est de l'ordre de \(\frac1{d^2}\)¹⁵. Pour simplifier, on va ignorer toutes les constantes désagréables, et dire que l'intensité lumineuse est exactement \(\frac1{d^2}\text{.}\)

Prenons maintenant un cercle de périmètre \(N\in\mathbb N\) et plaçons-y \(N\) étoiles régulièrement espacées. Puis on s'assoit sur un point \(P\) (sans étoile) quelque part sur le cerle. La longueur du cercle entre nous et l'étoile la plus proche est un réel \(x\in]0,\frac 12]\text{.}\)

On va se demander quel est l'intensité lumineuse totale que l'on perçoit depuis le point \(P\)¹⁷. On note \(f_N(x)\) cette intensité lumineuse totale.

Exercice 3.4. Etape 2: une seule étoile proche.

On part, modestement, d'une seule étoile \(R\) placée sur un cercle de périmètre 1.

Montrer que

\begin{equation*} f_1(x)=\left(\frac{\pi}{\sin(\pi x)}\right)^2. \end{equation*}

Indice.

Rappelons à tout hasard la définition d'un radian:

On pourra aussi utiliser le triangle \(POR\text{,}\) où \(O\) serait le centre du cercle.

Spoiler.

Pour passer d'une seule malheureuse étoile à une belle constellation à \(N\) étoiles, on va utiliser un théorème de géométrie adapté.

Exercice 3.5. Etape 3: le théorème de Pythagore inversé.

Considérons un triangle \(ABC\) rectangle en \(C\)²⁰. On note \(a=CB\text{,}\)\(b=AC\) et \(c=AB\text{,}\) et \(h\) la longueur de hauteur du triangle issue de \(C\text{.}\)

Montrer que

\begin{equation*} \frac1{h^2}=\frac1{a^2}+\frac1{b^2} \end{equation*}

Indice.

Calculer l'aire de \(ABC\) de deux façons différentes et utiliser le théorème de Pythagore classique pour calculer \(\frac1{a^2}+\frac1{b^2}\text{.}\)

Spoiler.

En utilisant ce théorème, on va voir que le passage d'une étoile sur un cercle de périmètre 1 à deux étoiles sur un cercle de périmètre 2 ne change pas la luminosité.

Exercice 3.6. Etape 4: Deux étoiles plus lointaines.

(a)

On part d'un cercle de périmètre 1 portant une étoile en \(R\text{.}\) De là, on trace un cercle \(C_2\) de périmètre 2 centré au point diamétralement opposé à l'observateur \(P\text{.}\) Puis on trace le diamètre de \(C_2\) qui passe par \(R\) et on appelle \(S_1\) et \(S_2\) les points d'intersection avec \(C_2\text{,}\) avec \(S_1\) plus proche de \(P\) que \(S_2\text{:}\)

Montrer que les distances \(x\) (distance entre \(P\) et \(R\) sur le cercle \(C_1\)) et \(y\) (distance entre \(P\) et \(S_1\) sur le cercle \(C_2\)) sont égales.

Indice.

On peut en utiliser le lien entre \(x\) et \(y\) et les mesures en radians d'angles bien choisis, ainsi que le théorème de l'angle au centre²¹.

Spoiler.

(b)

En déduire que \(f_1(x)=f_2(x)\text{.}\)

Indice.

Utiliser le théorème de Pythagore inversé dans le triangle \(S_1S_2B\text{.}\)

Spoiler.

Vers l'infini et au delà

En généralisant cette construction, on voit qu'en partant de \(N\) étoiles sur un cercle de périmètre \(N\text{,}\) on peut construire un système à \(2N\) étoiles sur un cercle de périmètre \(2N\text{:}\)

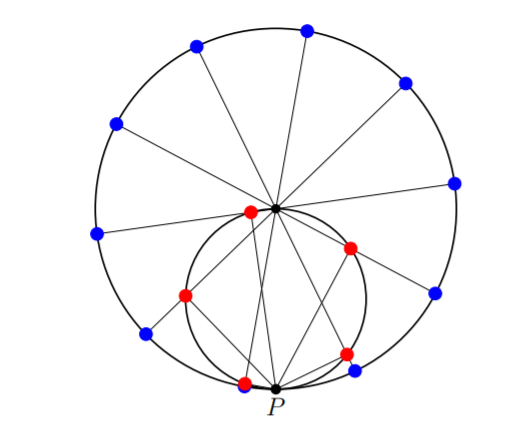
Et cela ne change pas la luminosité: chaque paire d'étoiles obtenues à partir d'une étoile du petit cercle donne la même luminosité totale que l'étoile initiale. Autrement dit, pour tout \(N\) et pour tout \(x\text{,}\)

Donc, si on part d'une seule étoile et qu'on fait ça \(p\) fois, on trouve:

Et on peut prendre \(p\) aussi grand qu'on veut.

C'est là qu'on va "passer à la limite". Si on a \(2N\) étoiles sur un cercle de périmètre \(2N\text{,}\) les \(N\) étoiles les plus lointaines sont à distance plus grande que le rayon du cercle, qui vaut \(r=\frac{2N}{2\pi}= \frac{N}{\pi}\text{.}\)

Du coup, la luminosité totale qui nous vient de ces étoiles éloignées est majorée par \(N\times \frac1{r^2}= \frac{\pi^2}{N}\text{,}\) un terme qui tend vers 0 quand \(N\rightarrow \infty.\)

A l'étape suivante, on remplace ces \(N\) étoiles proches par \(2N\) étoiles sur un cercle deux fois plus grand, et on ignore les \(N\) plus lointaines, ce qui ajoute une erreur de \(N\times \frac1{(2r)^2}= \frac{\pi^2}{4N}\text{.}\)

Et ainsi de suite: à la \(k\)-ième étape, on ajoute encore une erreur de \(\frac{\pi^2}{4^kN}\text{.}\)

Quand \(k\rightarrow \infty\text{,}\) la luminosité des \(N\) étoiles qu'on "garde" commence à ressembler à la luminosité émise par \(N\) étoiles placées sur une droite de part et d'autre de \(P\text{:}\)

\(P\) ici est placé en \(x\) et les étoiles sont toutes distantes de \(1\text{:}\) elles sont sur les points entiers.

La luminosité totale reçue en \(P\) est alors approchée par

avec une erreur de majorée par

donc il existe un \(\Theta \in [0,\frac{4\pi^2}3]\) tel que

Enfin, pour tout \(k\in \mathbb N\text{,}\) \(f_N(x)=f_{2^k N}(x)\) donc

Et on conclut en se rappelant que \(f_N(x)=\left(\frac{\pi}{\sin(\pi x)}\right)^2\text{.}\)

Sous-section 3.4 Une dernière pour la route: avec des probas

On peut aussi démontrer cette formule avec des probabilités.

Exercice 3.7.

(a)

Soient \(X_1,X_2: \mathbb R \rightarrow \mathbb R^+\) deux variables aléatoires positives suivant la (demi-) loi de Cauchy²². Leur densité de probabilité est donc

\begin{equation*} f_{X_1}(t)=f_{X_2}(t)= \begin{cases} \frac2{\pi}\frac1{1+t^2} \amp\text{ si } t>0\\ 0 \amp\text{ si } t \leq0 \end{cases} \end{equation*}

Posons \(Y=\frac{X_1}{X_2}\text{.}\) Montrer que la densité de \(Y\) est donnée par

\begin{equation*} f_Y(u)=\int_0^\infty tp_{X_1}(tu)p_{X_2}(t)dt \end{equation*}

Spoiler.

(b)

En déduire que

\begin{equation*} f_Y(u)=\frac{4}{\pi^2}\frac{\ln(u)}{u^2-1} \end{equation*}

Indice.

Trouver deux réels \(a\) et \(b\) tels que

\begin{equation*} \frac1{1+t^2u^2}\frac1{1+t^2} = \frac{a}{1+t^2u^2}+\frac{b}{1+t^2} \end{equation*}

Spoiler.

(c)

Justifier que \(\mathbb P(0\leq Y\leq 1) = \frac12\text{.}\) En déduire que

\begin{equation*} \int_0^1 -\frac{\ln(u)}{1-u^2} du = \frac{\pi^2}8 \end{equation*}

Spoiler.

(d)

De là, montrer que

\begin{equation*} \sum_{n=0}^\infty \frac1{(2n+1)^2} =\frac{\pi^2}8 \end{equation*}

Indice.

Pour \(u\in ]0,1[\text{,}\) on a

\begin{equation*} \frac1{1-u^2}= \sum_{k=0}^\infty u^{2k} \end{equation*}

Spoiler.

(e)

En déduire que

\begin{equation*} \sum_{n=1}^\infty \frac1{n^2} = \frac{\pi^2}6 \end{equation*}

Indice.

En séparant les entiers pairs et impairs, montrer que, en notant \(S=\sum_{n=1}^\infty \frac1{n^2}\text{,}\)

\begin{equation*} S=\frac14 S + \sum_{n=0}^\infty \frac1{(2n+1)^2} \end{equation*}

Spoiler.

Puisque la série \(\sum \frac1{n^2}\) converge, on peut écrire:

\begin{equation*} S=\sum_{n=1}^\infty \frac1{n^2} = \sum_{k=1}^\infty \frac 1{(2k)^2} + \sum_{k=0}^\infty \frac 1{(2k+1)^2} \end{equation*}

Or, pour tout \(k\geq 1\text{,}\) \(\frac 1{(2k)^2} = \frac14 \frac{1}{k^2}\) donc

\begin{equation*} \sum_{k=1}^\infty \frac 1{(2k)^2} = \frac14\sum_{k=1}^\infty \frac 1{k^2} = \frac14 S \end{equation*}

donc

\begin{align*} \frac 34 S \amp = \sum_{k=0}^\infty \frac1{(2k+1)^2}\\ S \amp= \frac34 \sum_{k=0}^\infty \frac1{(2k+1)^2} \\ \amp = \frac43 \frac{\pi^2}{8}=\frac{\pi^2}{6} \end{align*}