Quelques aides-mémoires:

• Topologie des e.v.n.
• Continuité dans les espaces normés
• Calcul différentiel - définitions
• Calcul différentiel - méthodes

Topologie dans les espaces vectoriels normés

La topologie est l'étude d'espaces géométriques, que l'on s'autorise à déformer comme de la pâte à modeler, du moment qu'on ne déchire rien. C'est donc un domaine étrange, où les tasses peuvent devenir des doughnuts et où beaucoup de choses sont, en fait, sphériques.

Afin de garder un tant soit peu les pieds sur terre, on s'intéresse surtout dans ce module à des espaces topologiques respectables: les espaces vectoriels normés.

Comme vous l'avez certainement constaté, même avec ces précautions, les boules ne sont pas forcément celles que l'on croit. Quelques visualisations (interactives, si les dieux de l'informatique sont de votre côté) sont disponibles ici.

Instructions: Pour les utiliser, allez dans le menu "Cell" et cliquez sur "Run All". Puis remontez en haut de la page.
Le temps de chargement peut être un peu long !

Lorsqu'on étudie les propriétés topologiques des espaces vectoriels normés, les choses sont particulièrement intéressantes en dimension infinie, où l'on s'intéresse, par exemple, à des espaces de fonctions (comme par exemple l'espace des fonction continues). Ce que vous savez des suites de fonctions s'avère utile pour étudier ces propriétés topologiques, notamment l'équivalence de normes, ou la complétude d'espaces de fonctions.

Quelques exemples de tels espaces fonctionnels ici.

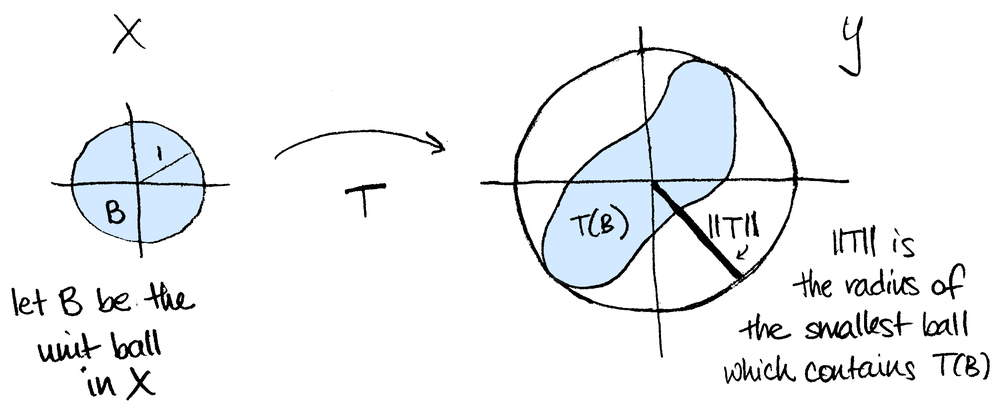
Enfin, une visualisation de la norme d'opérateur $\|T\| = \sup_{|x|=1}|T(x)|$ d'une application linéaire $T:X\rightarrow Y$ entre deux espaces vectoriels normés: (Source: Math3ma):

Différentiabilité dans les espaces vectoriels normés

By Usuwiki - Own work, CC BY-SA 4.0, Link

By derivative work: McSush Tangentialvektor.png: TN Public Domain, Link

Vous l'aurez peut-être noté, pour étudier des fonctions $\mathbb R \rightarrow \mathbb R$, la dérivée est un outil puissant, surtout quand il s'agit de problèmes de maximisation/minimisation. Il semble donc naturel de vouloir étendre cet outil aux fonctions dépendant de plusieurs variables (c'est-à-dire, définies sur $\mathbb R^n$) ou même aux fonctions définies sur un espace vectoriel normé quelconque.

On souhaiterait donc généraliser la "limite du taux d'accroissement" $\frac1h (f(a+h)-f(a))$ à une application $f: E \rightarrow F$ entre deux espaces vectoriels normés quelconques.

Problème: si $E$ n'est pas $\mathbb R$, $a$ et $h$ sont des vecteurs, et il est hors de question de diviser par $h$ ! Il faut donc se débarasser de cet encombrant dénominateur.

Une solution consiste à choisir un point $a$ de $E$, une "direction", c'est-à-dire un vecteur $v$ de $E$, et ne regarder que la façon dont $f$ varie dans cette direction. On se ramène alors, en quelque sorte, à une fonction d'une seule variable, $f(a+tv)$ pour $t$ réel, et on peut étudier $$ \lim_{t\rightarrow 0} \frac1t(f(a+tv)-f(a)) $$ SI cette limite existe, on dira que c'est la dérivée directionnelle de $f$ dans la direction de $v$. En particulier, si $E = \mathbb R^n$, on a des directions "privilégiées", données par les vecteurs de la base canonique: on retrouve alors les dérivées partielles.

Considérons $a=(1,2), v=(1,1)$ et $$\begin{align*} f:\mathbb{R}^2 & \rightarrow\mathbb{R}\\ (x,y)& \mapsto x^2-y^3 \end{align*}$$

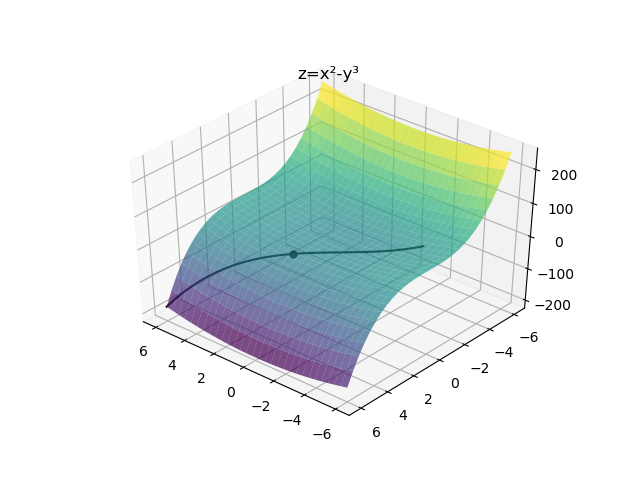
Alors on a $$ \begin{align*} \frac{f(a+tv)-f(a)}{t}& =\frac1t((1+t)^2-(2+t)^3 - (-7))\\ & =\frac1t(-10t-5t^2-t^3)\\ & =-10-5t-t^2 \\ & \xrightarrow[t\rightarrow 0]{}-10=\frac{\partial f}{\partial v}(a) \end{align*}$$

Visualisation par ici !

Dans $E=\mathbb{R}^n$, il y a des directions "spéciales": celles de la base canonique. Les dérivées directionnelles dans ces directions s'appellent dérivées partielles de la fonction.

Reprenons la fonction $$ \begin{align*} f:\mathbb R^2 &\rightarrow\mathbb R\\ (x,y)&\mapsto x^2-y^3 \end{align*} $$

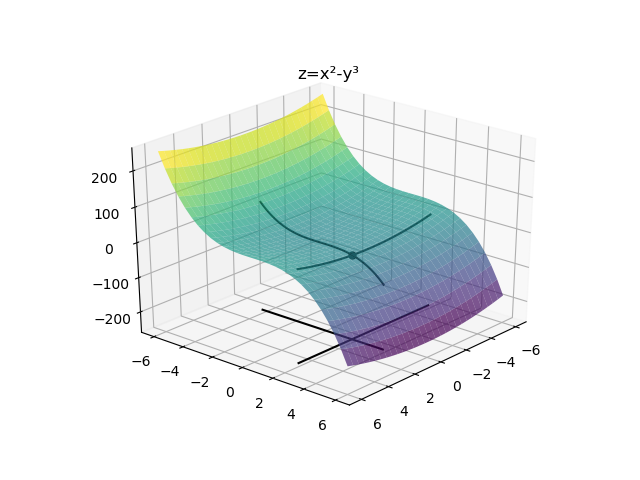
Alors on a $$ \begin{align*} f((x,y)+te_1)-f(x,y)&=(x+t)^2-y^3 -(x^2-y^3)\\ &=2xt+t^2\\ \text{et } f((x,y)+te_2)-f(x,y)&=x^2-(y+t)^3 -(x^2-y^3)\\ &=-3y^2t-3yt^2-t^3 \end{align*} $$

donc $\frac{\partial f}{\partial x}(x,y)=2x$ et $\frac{\partial f}{\partial y}(x,y)=-3y^2$.

Toutefois, et c'est justement la difficulté du calcul différentiel dans $E$ par rapport à $\mathbb R^n$, des directions.... il y en a un paquet. On voudrait donc trouver un "véritable" analogue de la dérivée, qui résume toutes les informations sur les variations de $f$ en un seul "objet". La question est, quel est cet objet ?

Revenons aux fonctions réelles d'une seule variable. Le nombre dérivé $f'(a)$ a une interprétation géométrique: c'est la pente de la tangente à la courbe de $f$ en $a$. Autrement dit, la droite $y=f(a) + f'(a)(x-a)$ est la droite qui approxime le mieux $f$ quand $x$ est proche de $a$, c'est à dire quand $x-a$ est petit.

Et c'est là la Grande Idée du Calcul Différentiel: ce qu'on veut, c'est approcher $f$ par une application linéaire, plus simple.

Pour cela, on cherche donc une application linéaire $L: E \rightarrow F$ telle que $f(a) + L(x-a)$ approxime bien $f$ quand $x$ est proche de $a$. Autrement dit, en notant $h=x-a$ le (petit) accroissement considéré, on cherche $L$ telle que, pour tout $h\in E$ assez petit, $$ f(a+h)=f(a)+ L(h)+R(h) $$ où le reste $R(h)$ est un $o(\|h\|)$, c'est à dire tend vers 0 plus vite que $h$. Si on peut faire ça, on dit que $f$ est différentiable, et $L$ est sa différentielle en $a$.

Si $E=\mathbb{R}^n$ et $F=\mathbb{R}^p$, l'application linéaire $L \in \mathcal{L}(\mathbb{R}^n,\mathbb{R}^p)$ peut être représentée par une matrice qu'on appelle la matrice jacobienne, notée $Jac_f(a)$.

Alors, la $j$-ième colonne de $Jac_f(a)$ est donnée par les coordonnées du $Df(a)(e_j)$ dans la base canonique de $\mathbb R^p$.

Or, $Df(a)(e_j)=\frac{\partial f}{\partial x_j}(a)=(\frac{\partial f_1}{\partial x_j}(a),\ldots,\frac{\partial f_p}{\partial x_j}(a))$

La matrice jacobienne est donc donnée par $$ Jac_f(a)= \begin{pmatrix} \frac{\partial f_1}{\partial x_1}(a)&\dots&\frac{\partial f_1}{\partial x_n}(a)\\ \vdots&\ddots&\vdots\\ \frac{\partial f_p}{\partial x_1}(a)&\dots&\frac{\partial f_p}{\partial x_n}(a)\\ \end{pmatrix} $$

• La $i$-ème ligne de $Jac_f(a)$ est la matrice de $Df_i(a)\in \mathcal L(\mathbb R^n,\mathbb R)$.
• La $j$-ième colonne de $Jac_f(a)$ est la $j$-ème dérivée partielle $\frac{\partial f}{\partial x_j}(a)\in\mathbb R^p$.

Par linéarité, pour tout $v=(v_1\ldots,v_n)\in\mathbb R^n$, on a donc $$ Df(a)(v)=\sum_{i=1}^n v_i \frac{\partial f}{\partial x_i}(a). $$

Ci-dessous, un diagramme résumant comment ces différentes définitions interagissent:

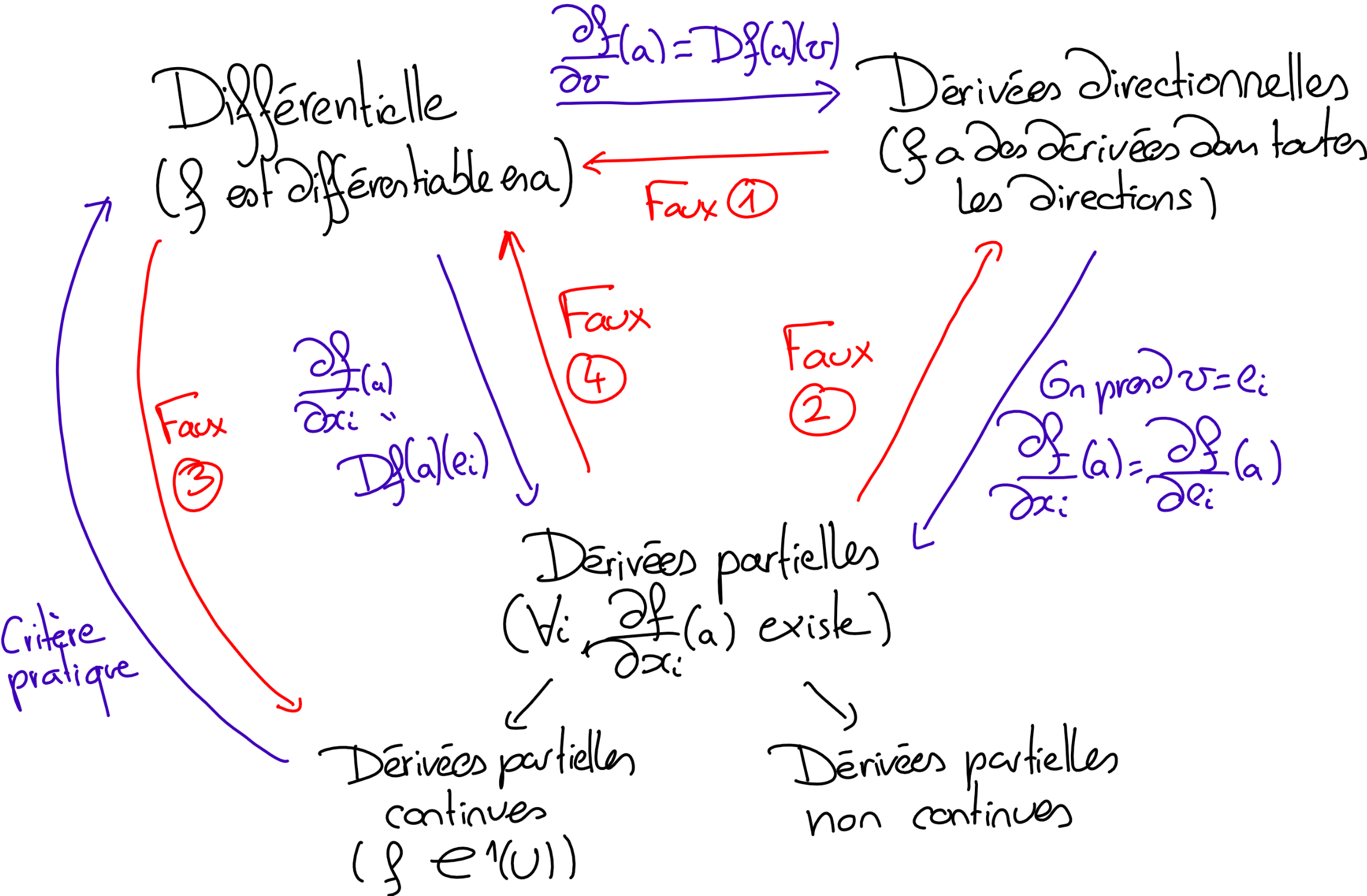
Les contre-exemples 1,2,3 et 4 du diagramme sont explicités ici.

Inversion locale et fonctions implicites

On l'a dit, la Grande Idée du Calcul Différentiel, c'est que l'algèbre linéaire c'est super. Donc, on essaie d'approximer localement nos fonctions par une application linéaire, qu'on appelle la différentielle.

La question qu'on va se poser ici, c'est comment cette idée peut aider à résoudre des équations.

Ainsi, si on prend un système (non linéaire) à $p$ équations, d'inconnue $x\in \mathbb R^n$ $$ \begin{cases} f_1(x_1,\ldots,x_n)&=u_1\\ \vdots\\ f_p(x_1,\ldots,x_n)&=u_p \end{cases} $$ et si $f$ est différentiable, alors on peut se ramener localement à un système linéaire. Et ça, on sait résoudre:

• il y a une unique solution si $n=p=$ rang du système
• il y a une infinité de solutions, décrites par des variables paramètres, si $n>p$.

Les deux grands théorèmes dont on va parler, le théorème d'Inversion Locale (TIL) et le théorème des Fonctions Implicites (TFI), précisent ce qu'on peut obtenir dans chacun de ces deux cas:

• Le Théorème d'Inversion Locale s'applique dans le cas $n=p$: à quelle condition peut-on "inverser" le système, c'est à dire résoudre $f(x)=u$ en $x=f^{-1}(u)$ ?
• Le Théorème des Fonctions Implicites s'applique dans le cas $n>p$: à quelle condition peut-on choisir des variables "paramètres" $z_{p+1},\ldots,z_n$ et résoudre $f(x,z)=0$ en $x=\psi(z)$ ?

Quelques polycopiés:

• Cours sur les théorèmes d'Inversion locale et fonctions implicites
• Preuve du Théorème d'inversion locale: Régularité de l'inverse
• Preuve du théorème des fonctions implicites
• Cours sur le Théorème des Extrema liés
• Théorème des extrema liés à plusieurs contraintes
• Quelques applications du TFI en optimisation

Heuristique du TIL

Cas linéaire Soit $f:\mathbb R^n\rightarrow \mathbb R^p$ une application linéaire.
Alors l'équation $y=f(x)$ a une unique solution $x\in\mathbb R^n$ si, et seulement si, $n=p$ et si la matrice $A$ de $f$ dans la base canonique de $\mathbb R^n$ est inversible.

D'un point de vue différentiel, dans ce cas, pour tout $x\in \mathbb R^n$, $Df(x)=f$ et $Jac_f(x) = A$.

$\leadsto$ On a donc $f$ inversible ssi $Df(x)$ inversible.

Cas différentiable Soient $f:U\subset \mathbb R^n \rightarrow \mathbb R^n$ $\mathcal C^1$, $x_0\in U$ et $y_0=f(x_0)$.

On souhaite résoudre $f(x)=y$ pour $(x,y)$ proches de $(x_0,y_0)$. Posons donc $y=y_0+k$ et cherchons $x$ sous la forme $x_0+h$. Alors $f(x)=y$ se réécrit $f(x_0+h)=y_0+k$: $$ f(x_0)+ Df(x_0)(h) \simeq y_0+k=f(x_0)+k $$ donc, si $Df(x_0)$ est inversible, la solution est donnée par $$ \begin{align*} f^{-1}(y)& = x_0+h=x_0+Df(x_0)^{-1}(k)+\text{chouïa}\\ &= f^{-1}(y_0)+Df(x_0)^{-1}(y-y_0)+\text{chouïa} \end{align*} $$

Plus qu'à rigorifier tout ça !

Un contre-exemple si on suppose seulement que $f$ est dérivable, et non $\mathcal C^1$:

Heuristique du Théorème des Fonctions Implicites

Cas linéaire: Considérons par exemple le système $$ (\mathcal S) \begin{cases} x+y+z&=0 \\ 2x+2y+z&=1 \end{cases} \iff \begin{cases} x+y+z&=0\\ \phantom{x+{}}x+y&=1 \end{cases} \iff \begin{cases} z&=-1\\ y&=1-x \end{cases} $$ $\leadsto$ L'ensemble des solutions de $(\mathcal S)$ est le graphe $\{(x,\varphi(x)),x\in\mathbb R\}$ de la fonction $\varphi:x\in \mathbb R \mapsto (1-x,-1)\in\mathbb R^2$.

En prime, pour savoir combien d'inconnues mettre en paramètre et lesquelles, on dispose de l'algorithme du pivot de Gauss, qui nous permet d'échelonner le système.

Quel est le bon critère pour faire ça quand les équations ne sont pas linéaires ?

Découpons la jacobienne. Pour $f$ une application $\mathcal C^1$ sur $\mathbb R^n=\mathbb R^{n-p} \times \mathbb R^p$: $$ \begin{align*} f:\mathbb R^{n-p} \times \mathbb R^p &\rightarrow \mathbb R^p \\ (x,y)&\mapsto f(x,y) \end{align*} $$ on décompose la jacobienne de $f$ en deux parties:

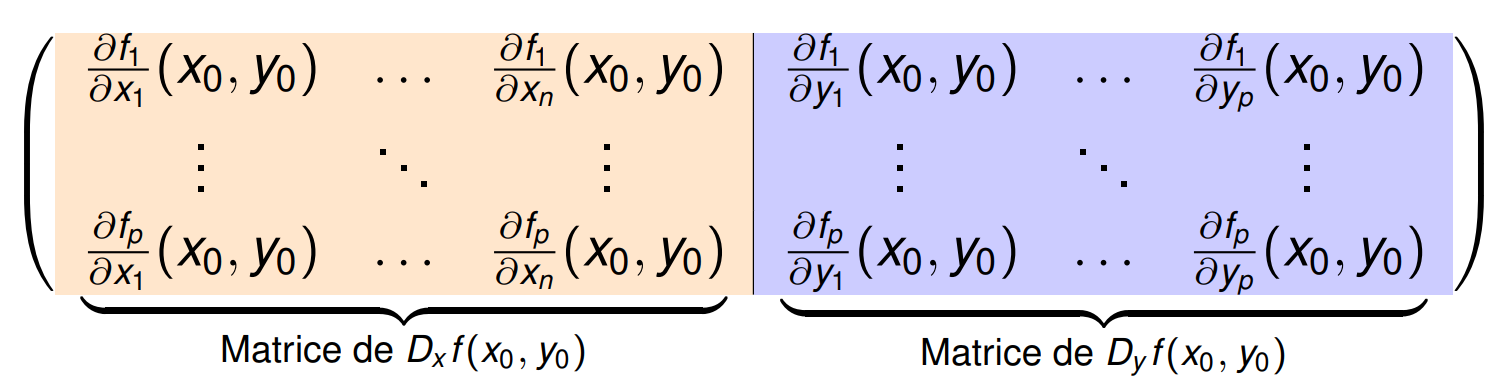
On a donc, pour $(h,k)\in \mathbb R^n\times \mathbb R^p$,

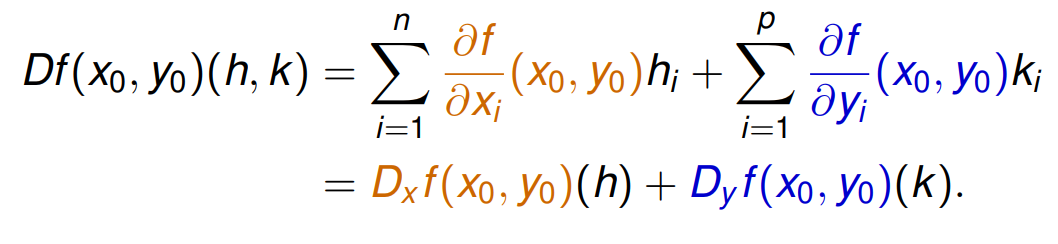
Supposons que $f(x_0,y_0)=0_{\mathbb R^p}$ et résolvons l'équation $f(x,y)=0$ près de $(x_0, y_0)$ en fonction de $x$.

Autrement dit on cherche $\varphi:V\subset\mathbb R^n\rightarrow\mathbb R^p$ telle que $$ f(x,y)=0 \iff y=\varphi(x). $$ Or, au voisinage de $(x_0,y_0)$, on a $$ \begin{align*} f(x,y)&=f(x_0,y_0)+Df(x_0,y_0)(x-x_0,y-y_0)+\text{chouïa}\\ &=D_xf(x_0,y_0)(x-x_0)+D_yf(x_0,y_0)(y-y_0)+\text{chouïa} \end{align*} $$ Donc l'équation $f(x,y)=0$ se réécrit $$ D_y f(x_0,y_0)(y-y_0)=-D_xf(x_0,y_0)(x-x_0)+\text{chouïa} $$

$\leadsto$ Si $D_yf(x_0,y_0)$ est inversible, il y a une unique solution $$ y=\varphi(x)=y_0-(D_y f(x_0,y_0)^{-1}D_xf(x_0,y_0))(x-x_0)+... $$

Un exemple: $f:(x,y)\in\mathbb R \times \mathbb R \mapsto x^2+y^2-1 \in \mathbb R$:

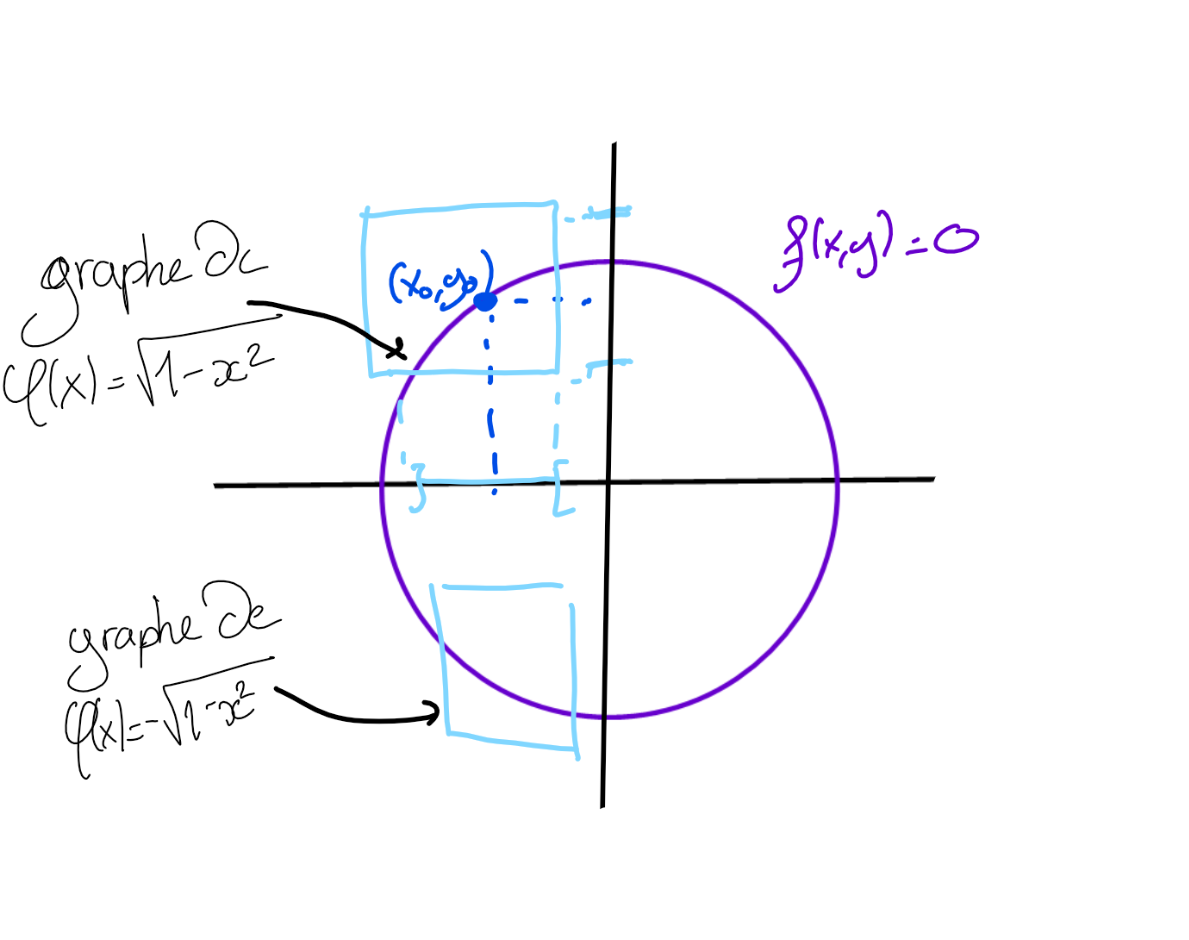
Plus qu'à rigorifier tout ça !

Sous-variétés

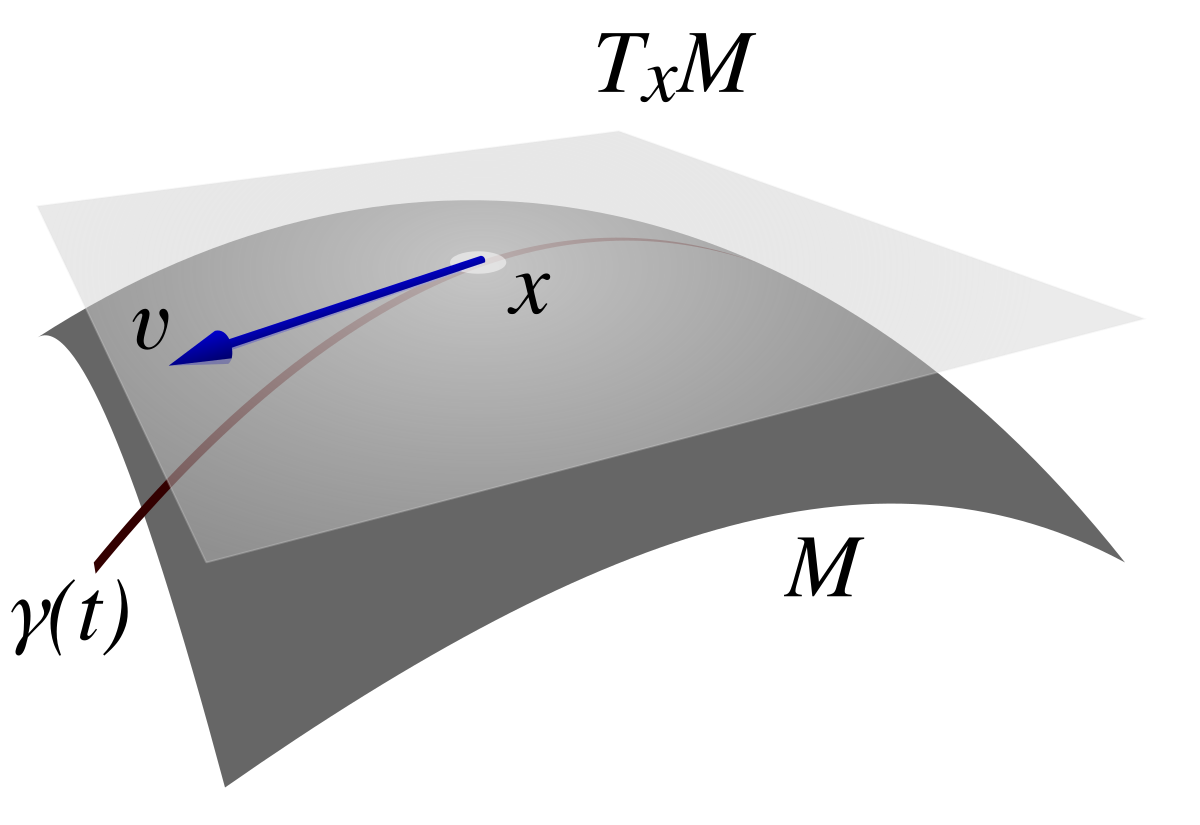
On peut pousser plus loin la Grande Idée du calcul différentiel, et s'intéresser à des espaces qui ne sont pas des espaces vectoriels, mais qui, localement, y ressemblent. Une sphère, par exemple: ce n'est pas un espace vectoriel, mais depuis la surface de la Terre, localement donc, on a quand même furieusement l'impression de marcher sur $\mathbb R^2$.

Etudier à quoi ressemblent de tels ensembles, ça s'appelle la géométrie différentielle. Une intro ici: