Quelques livres:

• Axler, Measure, Integration and Real Analysis, en anglais, mais très agréable à lire.

• Une référence en français: l'excellent polycopié de Thierry Gallay, disponible ici.
• Une autre référence, très complète: Analyse - Théorie de l'intégration de Gilles Pagès et Marc Briane, disponible à la bibliothèque.
• De l'intégration aux probabilités, par Olivier Garet et Aline Kurtzmann.
• Exercices corrigés en théorie de la mesure et intégration, de Jean-Pascal Ansel et Yves Ducel.

Quelques aide-mémoires:

• Ensembles, famille d'ensembles, cardinalité
• Intégrale de Riemann
• Permutations limite-intégrale
• Théorie de la mesure et intégration de Lebesgue

Quelques polycopiés:

• Cours sur les espaces $L^p$
• COurs sur l'espace hilbertien $L^2$
• De la théorie de la mesure aux probabilités: une petite traduction
• Construction des espaces $L^p$
• Un ensemble Lebesgue-mesurable qui n'est pas borélien
• Un ensemble non Lebesgue-mesurable
• Comparaison des intégrales de Lebesgue et de Riemann
• De la tribu de Borel à celle de Lebesgue
• Intégrale de Stieltjes

Construction d'une nouvelle intégrale : Pourquoi changer une équipe qui gagne ?

Dans les temps anciens, c'est-à-dire à partir de 1868, les mathématiciens pouvaient intégrer toutes sortes de fonctions, grâce aux travaux de Riemann. Son intégrale couvrait toutes sortes de cas raisonnables: les fonctions continues, ou pas trop horriblement discontinues, les fonctions monotones, etc. Avec un peu de travail, même certaines fonctions non bornées ou limites de suites de fonctions étaient abordables.

Mais tout le monde n'était pas satisfait de cet état de fait. Certes, l'intégrale de Riemann permet de calculer l'aire sous la courbe des fonctions les plus communes, mais ne peut faire face à des ennemis plus puissants, comme la fonction indicatrice des rationnels.

Et ce n'est même pas une fonction si compliquée: elle ne prend que deux valeurs !

D'accord, il y a quelques aberrations tordues qui nous échappent, mais ce n'est pas comme si on se réveillait tous les quatre matins avec une furieuse envie d'intégrer l'indicatrice des rationnels.

C'est vrai, mais il y a plus gênant: le cas des suites de fonctions inoffensives mais dont la limite n'est subitement plus intégrable. Il y a, bien sûr, quelques théorèmes de convergence, mais leurs hypothèses (intégrabilité de la fonction limite, convergence uniforme sur un intervalle fermé borné) semblent terriblement restrictives.

Les ennuis ne s'arrêtent pas là. Les fonctions non bornées s'intègrent via un procédé de passage à la limite (intégrales généralisées) qui s'effondre s'il y a trop de points de tension.

Et c'est un problème, car tout l'art martial des analystes repose sur des passages à la limite. Pour s'attaquer à un problème ardu, le plus efficace est souvent de le découper en morceaux, approcher chaque morceau par un plus simple, et passer à la limite. Ainsi la dérivée est la limite du taux d'accroissement sur de petits morceaux de courbe, et l'intégrale de Riemann est une limite de sommes d'aires de rectangles.

Ne pas pouvoir facilement passer à la limite dans une intégrale, outre les douleurs causées aux mages novices de deuxième année, est donc un désavantage stratégique. D'autant plus que l'intégration paraît être l'outil clé des probabilités continues, or les probabilités reposent, encore plus que le reste, sur des passages à la limite !

C'est vrai, mais la terrible réalité est qu'on ne sait pas calculer l'aire de grand chose. En fait, dès que les bords ne sont pas droits, c'est tout de suite très pénible. L'intégrale de Riemann nous permet d'intégrer toutes les fonctions dont l'aire sous la courbe peut s'approximer par des rectangles, mais comment va-t-on faire mieux ?

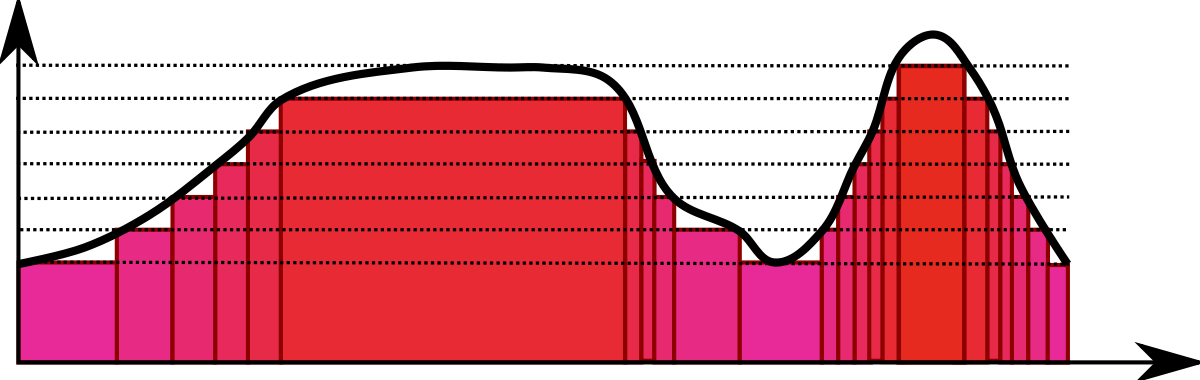
C'est là qu'intervient Emile Borel. Comment construit-on l'intégrale de Riemann d'une fonction $f:[a,b]\rightarrow \mathbb R$, au juste ? On découpe $[a,b]$ en petits sous-intervalles $[x_i, x_{i+1}]$, et on approche de l'aire sous la courbe de $f$ par la somme $$I(f, (x_0,x_1,\dots,x_n)) = \sum_{i=0}^{n-1} (x_{i+1}-x_i)\inf_{[x_i, x_{i+1}]}f$$

On approche l'aire sous la courbe de $f$ par une somme de longueurs d'intervalles multipliées par la borne inférieure des valeurs de $f$ sur chaque intervalle.

Ce que suggère Borel, c'est que, si on savait mesurer la longueur d'autres ensembles que des intervalles, on pourrait alors découper l'intervalle en morceaux plus compliqués, qui tiennent compte des valeurs de la fonction.

Cela pourrait permettre de coller mieux aux spécificités de la fonction: par exemple, la fonction indicatrice ne prend que deux valeurs, donc il suffirait de savoir mesurer l'ensemble $A=\mathbb Q \cap [0,1]$, où elle vaut 1, et l'ensemble $B=[0,1]\setminus \mathbb Q$, où elle vaut 0. Et alors on pourrait dire que $$\int_0^1 1_{\mathbb Q}(t) dt = m(A)\cdot 1 + m(B)\cdot 0.$$

Et plus généralement:

Ainsi, au lieu de le débiter en sous-intervalles $\{x\in I, t_i< x \leq t_{i+1} \}$ le long d'une partition, on pourrait le découper en $\{x\in I, y_i< f(x) \leq y_{i+1} \}=f^{-1}(]y_i,y_{i+1}])$. Par exemple, pour l'indicatrice des rationnels, on découpe en $1_{\mathbb Q}^{-1}(]-\frac12,\frac12[)=[0,1]\setminus \mathbb Q$ et $1_{\mathbb Q}^{-1}(]\frac12,\frac32[)=\mathbb Q \cap [0,1]$.

Ce qu'Henri Lebesgue résume par:

Imaginez que je dois payer une certaine somme; je peux sortir les pièces de mon porte monnaie comme elles viennent pour arriver à la somme indiquée, ou sortir toutes les pièces et les choisir selon leur valeur. La première méthode est l'intégrale de Riemann, la deuxième est mon intégrale.

On découpe ainsi l'aire sous la courbe de $f$ en "rectangles" dont la base n'est plus un intervalle, mais un sous-ensemble de $\mathbb R$ donné par $f^{-1}(]y_i,y_{i+1}])$. Ce qu'il nous faut, c'est donc une façon de mesurer la "longueur" de tels ensembles, comme on sait le faire pour les intervalles. Il nous faut...

La théorie de la mesure

Le but de la théorie de la mesure est, comme le nom l'indique, de "mesurer" des parties de $\mathbb R$. Autrement dit, à sous-ensemble $A \subset \mathbb R$, on veut associer un nombre positif qui représente sa mesure.

Il y a plusieurs de façons de faire: par exemple, on pourrait définir la mesure d'une partie $A$ comme son nombre d'éléments. C'est le plus naturel sur $\mathbb N$ (ou, de manière générale, sur les ensembles discrets), et c'est ce que l'on appelle la mesure de comptage. Mais dans $\mathbb R$, il y a beaucoup plus d'éléments et de "types" de sous-ensembles, et si on se contente de compter, la plupart des sous-ensembles "intéressants", comme les intervalles, vont avoir une mesure infinie, ce qui ne nous éclaire pas beaucoup.

Qui plus est, on voudrait utiliser cette notion de mesure pour généraliser l'intégrale des fonctions au sens de Riemann. On veut donc garder tel quel ce qui marche déjà, donc on veut que la mesure d'un intervalle $[a,b]$, $]a,b[$ ou $]a, b]$ soit sa longueur, $b-a$. C'est la première exigence.

Pendant qu'on y est, il y a quelques autres propriétés qui sembleraient raisonnables: notamment l'additivité, autrement dit, on demande que la mesure d'une union de sous ensembles disjoints soit la somme de la mesure de ces sous-ensembles. Ou encore, l'invariance par translation: on demande que la mesure d'un ensemble reste la même si on le décale d'une quantité fixée.

Plot twist: il n'existe aucune fonction $m: \mathcal P(\mathbb R)\rightarrow [0, +\infty]$ telle que

• si $I$ est un intervalle, $m(I)$ est sa longueur,
• si $(A_n)_n$ est une famille dénombrable de parties disjointes de $\mathbb R$, alors $m\left(\bigcup A_n\right)= \sum_n m(A_n)$,
• pour toute partie $A$ de $\mathbb R$, pour tout $t\in \mathbb R$, $m(A+t)=m(A)$.

Borel et Lebesgue ont perdu cette bataille, mais ils n'ont pas perdu la guerre. Il est impératif de garder les trois propriétés naturelles. Stratégiquement, s'il faut renoncer à quelque chose, c'est à définir $m$ sur $ \mathcal P(\mathbb R)$ tout entier. Le problème de $ \mathcal P(\mathbb R)$, c'est que c'est un ensemble absolument monstrueux, qui contient toutes sortes de sous-ensembles bizarres. Par exemple, les ensemble de Cantor, gros ou maigres. Et ce ne sont même pas les plus échevelés.

Il faut donc se restreindre à un sous-ensemble $\mathscr T$ de $\mathcal P(X)$ qui contient des gens respectables. De plus, pour garder les propriétés exigées, $\mathscr T$ doit être stable par union dénombrable. On souhaiterait aussi pouvoir passer au complémentaire (si on sait mesurer une partie, on doit bien pouvoir mesurer ce qui reste). Et, au minimum, on doit pouvoir mesurer $\emptyset$ (quand même).

Quand, dans la jungle impénétrable des parties de $\mathbb R$, un sous-ensemble $\mathscr T \subset \mathcal P(\mathbb R)$ vérifie ces trois propriétés, on dit que c'est une tribu.

On veut aussi, bien sûr, que l'ensemble de définition de $m$ contienne tous les intervalles.
Et là, un topologue sort de derrière un palétuvier en s'exclamant: les intervalles sont les "boules" de la topologie usuelle sur $\mathbb R$. Les ouverts et les fermés qu'on définit à partir de ces boules doivent être mesurables !

On considère donc la tribu la plus économique qui contienne tous les ouverts de $\mathbb R$: c'est ce que l'on appelle la tribu borélienne.

Cette fois, c'est une victoire: sur la tribu des boréliens, il existe une application $m$ à valeurs dans $0, +\infty]$, qui, tel un génie, exauce nos trois souhaits. On l'appelle la mesure de Borel. On peut l'étendre à une tribu plus grande (la tribu de Lebesgue) et on l'appelle alors mesure de Lebesgue (dans les deux cas, il s'agit de la mesure extérieure restreinte à une tribu appropriée).

Une jolie application de la théorie de la mesure à la musique, basée sur la longueur des intervalles:

Pour en savoir (encore) plus, je vous renvoie vers la série d'articles sur la théorie de la mesure d'Infinity Plus One:

• How long is infinity ?
• The Cantor Set
• Non measurable sets

Des exemples pour illustrer cette théorie de la mesure sont disponible par ici.

Armés de cette mesure, Borel, Lebesgue et leurs disciples construisirent une nouvelle intégrale, plus puissante, permettant de dépasser les faiblesses de l'intégrale de Riemann.

Plus de détails dans cette vidéo (en anglais):

Un des grands atouts de cette nouvelle intégrale est la facilité de passage à la limite, illustrée par 3 théorèmes majeurs:

• Le Théorème de Convergence Monotone;
• Le Lemme de Fatou;
• Le Théorème de Convergence Dominée;

Les deux premiers sont de puissants leviers théoriques; nombre de théorèmes d'intégration se terminent par la formule rituelle "On conclut par convergence monotone. Amen." Le dernier, souvent utilisé dans les exemples, permet de traiter de nombreux problèmes de passage à la limite. Pas tous, cependant: le passage à la limite sous l'intégrale reste une entreprise risquée. Le site Math3ma offre d'excellents contre-exemples illustrés:

• Une suite qui converge presque partout, mais dont l'intégrale ne converge pas
• Une suite qui converge uniformément, mais pas en norme intégrale
• Une suite de fonctions toutes intégrables, convergeant uniformément vers une limite non intégrable
• Une suite qui converge simplement (point par point), mais pas en norme intégrale
• Une suite dont les intégrales convergent, mais qui ne converge en aucun point.

Espaces de Lebesgue

A l'aide de l'intégrale de Lebesgue, on peut constuire une certaine catégorie d'espaces fonctionnels (c'est-à-dire d'espaces vectoriels normés dont les éléments sont des fonctions), définis à partir d'intégrales.

Pourquoi faire ? L'idée de l'analyse fonctionnelle est de décrire de tels espaces vectoriels, de façon à pouvoir étudier des questions sur les fonctions en termes d'algèbre linéaire et de topologie sur les espaces vectoriels normés.

Ainsi, on peut aborder la résolution d'une équation aux dérivées partielles, par exemple $$ \frac{\partial u}{\partial t} = k\frac{\partial^2 u}{\partial x^2} $$ en se demandant: pour quel choix de norme sur les espaces vectoriels $\mathcal C^2(\mathbb R^2,\mathbb{R})$ et $\mathcal C^0(\mathbb R^2,\mathbb{R})$ l'application linéaire $D: u\in\mathcal C^2(\mathbb R^2,\mathbb{R}) \mapsto \frac{\partial u}{\partial t} - \frac{\partial^2 u}{\partial x^2}\in \mathcal C^0(\mathbb R^2,\mathbb{R})$ est-elle continue ?

Ou encore, quelles sont les valeurs propres de l'application linéaire $u\mapsto \frac{\partial^2 u}{\partial x^2}$ ? Peut-on décomposer toute fonction comme somme de vecteurs propres ?

Dans le cadre de l'analyse fonctionnelle, les espaces vectoriels qui nous intéressent sont de dimension infinie, donc toutes les normes n'y sont pas équivalentes: d'où l'intérêt de choisir "la bonne norme" pour étudier un problème donné.

Pour pouvoir utiliser les plus puissants théorèmes sur les e.v.n., comme par exemple le théorème du point fixe, une des conditions essentielle est la complétude de l'espace vectoriel. Sur un espace vectoriel $E$, on va donc particulièrement rechercher des normes telles que l'e.v.n. $(E,\|.\|)$ soit un espace de Banach.

Un exemple de cette idée ici: deux normes sur $\mathcal C^0$.

C'est encore mieux si la norme est obtenue à partir d'un produit scalaire sur $E$, car on dispose alors des notions d'endomorphismes autoadjoints (qui sont diagonalisables en dimension finie, et demeurent sympathiques en dimension infinie) et surtout de projection orthogonale. Un espace euclidien complet $(E, \langle .,.\rangle)$ est appelé un espace de Hilbert.

Et donc, les espaces de Lebesgue: vous connaissez déjà l'ensemble $\mathscr L^0$ des fonctions réelles mesurables, ainsi que l'ensemble $\mathscr L^1$ des fonctions intégrables, c'est-à dire telles que $$\int_{\mathbb R} |f| d\lambda < \infty$$
Pour $p>1$, on va s'intéresser à l'ensemble $$ \mathscr L^p=\{f\in \mathscr L^0, \int_\mathbb{R} |f|^p d\lambda < \infty\} $$ sur lequel on peut donc définir une "norme" $$ \|f\|_p = \left(\int_\mathbb{R} |f|^p d\lambda\right)^\frac1p $$

Pourquoi les guillemets ? $\|.\|_p$ n'est pas tout à fait une norme sur $\mathscr L^p$: il existe des fonctions, nulles Lebesgue-presque partout, telles que $\|f\|_p=0$ mais $f\neq 0$.

On peut contourner ce problème par un procédé de passage au quotient, qui nous donne un ensemble $L^p$ sur lequel $\|.\|_p$ est une vraie norme. De plus, ce sont des espaces de Banach: les $(L^p,\|.\|_p)$ sont appelés espaces de Lebesgue.

Et encore mieux, $L^2$, muni du produit scalaire $$\langle f,g\rangle = \int_\mathbb R fg d\lambda$$ est un espace de Hilbert.

Cours complet

Voir la Page 2 ci-dessous pour un cours complet, et la Page 3 pour une collection d'exercices corrigés.