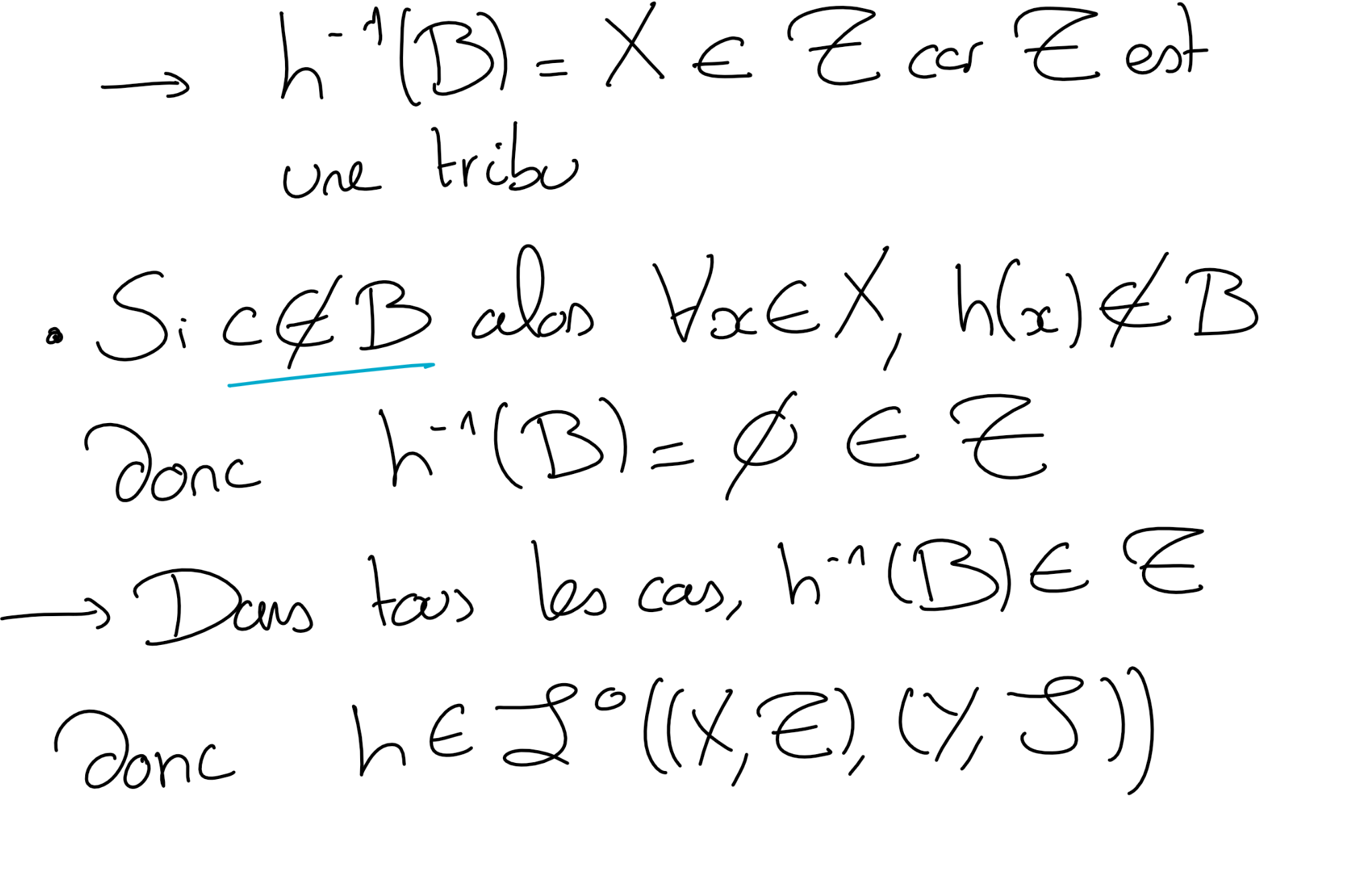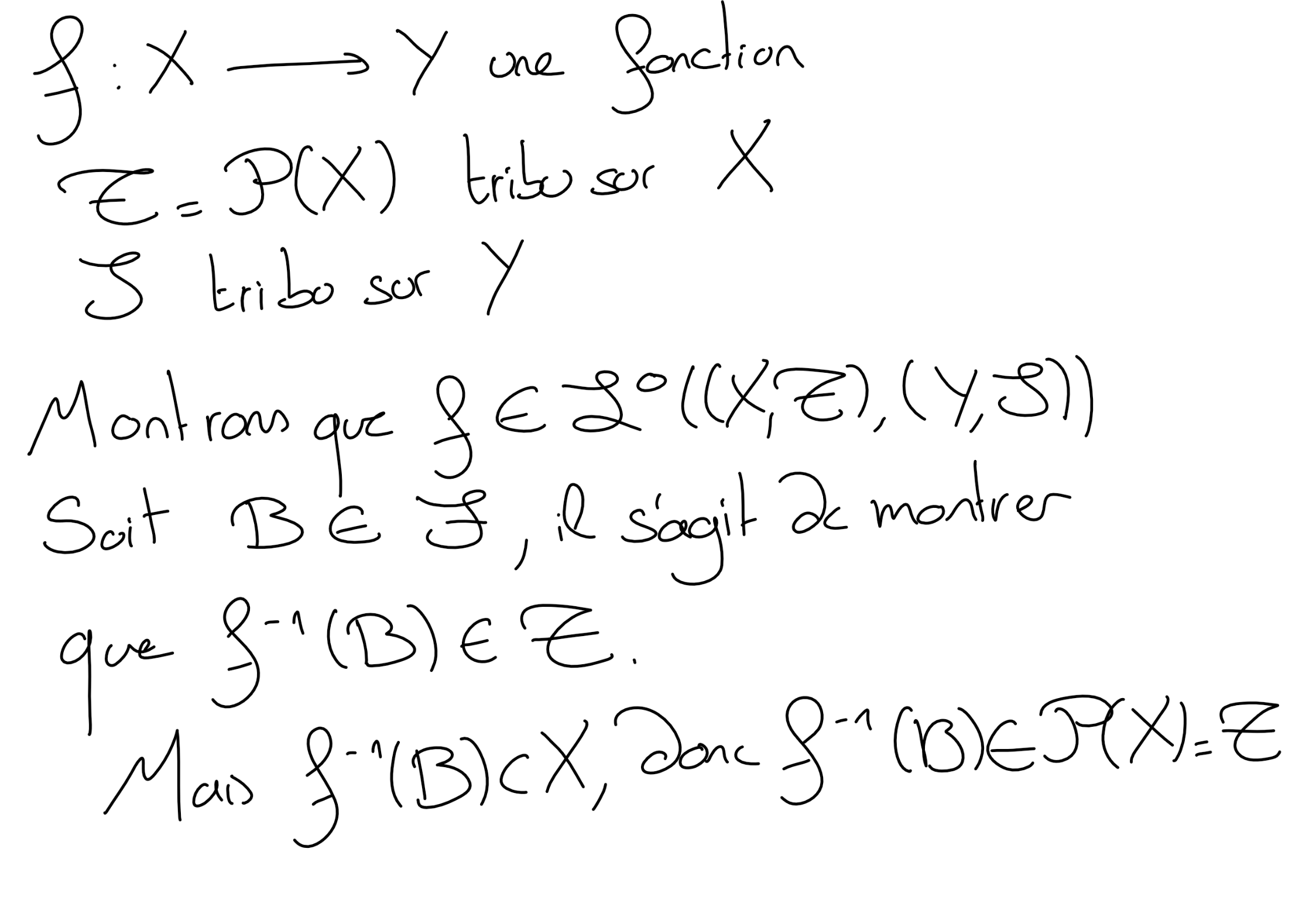Exemples en théorie de la mesure et de l'intégration

Section 7 Fonctions mesurables

Rappel: Si \(f:X\rightarrow Y\) est une fonction, et \(B\subset Y\text{,}\) on peut définir l'ensemble \(f^{-1}(B)\) des antécédents des éléments de \(B\) par \(f\)¹, autrement dit:

(Même si la notation peut induire en erreur, l'existence d'une bijection réciproque \(f^{-1}\) n'est pas du tout nécessaire pour définir cet ensemble).

Soit \(h:X\rightarrow Y\) une fonction constante. Montrer que, quelle que soit la tribu \(\mathscr T\) sur \(X\) et quelle que soit la tribu \(\mathscr S\) sur \(Y\text{,}\) \(h\) est mesurable de \((X,\mathscr T)\) dans \((Y,\mathscr S)\text{.}\)

Solution

Comme on va le voir dans les exercices ci-dessous, plus il y a de monde dans \(\mathscr T\) et moins il y en a dans \(\mathscr S\text{,}\) plus il y a de fonctions mesurables:

Project 7.1. Taille des tribus et mesurabilité.

(a)

Soit \((Y,\mathscr S)\) un ensemble mesuré. On munit \(X\) de la tribu \(\mathcal P(X)\text{.}\) Montrer que toute fonction \(f:X\rightarrow Y\) est mesurable de \((X,\mathcal P(X)\) dans \((Y,\mathscr S)\text{.}\)

Solution

(b)

Soit \((Y,\mathscr S)\) un ensemble mesuré tel que \(\mathscr S\) contient les singletons. On munit \(X\) de la tribu \(\{X,\emptyset\}\text{.}\) Montrer que, pour toute fonction \(f:X\rightarrow Y\text{,}\)

\begin{equation*} f\in \mathcal L^0((X,\{X,\emptyset\}),(Y,\mathscr S)) \iff f\text{ constante}. \end{equation*}

Solution

Reprenons la tribu \(\mathscr T_3\) de parties de \(\mathbb R\) définie à l'exemple Checkpoint 1.4:

\begin{equation*} \mathscr T_3=\{A\subset \mathbb R, A=-A\} \subset\mathcal P(\mathbb R) \end{equation*}

Montrer qu'une fonction \(f:\mathbb R \rightarrow \mathbb R\) est mesurable de \((\mathbb R,\mathscr T_3)\) dans \((\mathbb R,\mathscr B(\mathbb R))\)² si, et seulement si, elle est paire.

où \(\mathscr B(\mathbb R)\) désigne les boréliens de \(\mathbb R\)

Hint

On peut procéder par double implication: en supposant que \(f\) est paire, montrer que l'image réciproque de tout borélien est dans \(\mathscr T_3\text{,}\) i.e. est symétrique par rapport à 0. Réciproquement, si \(f\) n'est pas paire, alors il existe \(x\in \mathbb R\) tel que \(f(x)\neq f(-x)\text{.}\) Que donne alors l'image réciproque par \(f\) du borélien \(\{f(x)\}\) ? Contient-il \(-x\) ?

Solution

Soit \((X,\mathscr T\) un ensemble mesurable, et \(A\subset X\text{.}\) Reprenons la tribu \(\mathscr T_A\) de parties de \(X\) définie à l'exemple Checkpoint 1.5:

\begin{equation*} \mathscr T_A=\{B\in \mathscr T, A\subset B \text{ ou } A\cap B = \emptyset\} \subset\mathcal P(X) \end{equation*}

Montrer qu'une fonction \(f:X\rightarrow \mathbb R\) est mesurable de \((X,\mathscr T_A)\) dans \((\mathbb R,\mathscr B(\mathbb R))\) si, et seulement si, \(f\) est constante sur \(A\text{.}\)

Hint

On peut (encore) procéder par double implication: en supposant que \(f_{|A} =c\text{,}\) que peut on dire de l'image réciproque d'un borélien \(B\text{,}\) en séparant les cas \(c\in B\) et \(c\notin B\text{.}\) Réciproquement, si \(f\) n'est pas constante sur \(A\text{,}\) alors il existe \(a_1,a_2\in A\) tels que \(f(a_1)\neq f(a_2)\text{.}\) Il s'agit de trouver un borélien dont l'image réciproque intersecte \(A\) mais ne contient pas \(A\) en entier.

Solution

Soit \((X,\mathscr T)\) un espace mesuré. Rappelons que, si \((X_i)_{i\in I}\) est une partition au plus dénombrable de \(X\) telle que, pour tout \(i\in I\text{,}\) \(X_i\in \mathscr T\text{,}\) alors

où \(\mathscr T_i=\{X_i \cap A, A\in \mathscr T\}\) est la tribu-trace de \(\mathscr T\) sur \(X_i\text{.}\)

Project 7.2. Exemple 3: Partitions de \(X\).

(a)

Soit \(X\) un ensemble, \((X_i)_{i\in I}\) est une partition au plus dénombrable de \(X\text{.}\) On considère sur \(X\) la tribu \(\mathscr T\) engendrée par la partition \((X_i)\text{,}\) comme en Project 1.2 :

\begin{equation*} \mathscr T = \tau(\{X_i, i\in I\}) \end{equation*}

Soit \(f:X\rightarrow \mathbb R\) une fonction. Montrer que si \(f\) est mesurable de \((X,\mathscr T)\) dans \((\mathbb R,\mathscr B(\mathbb R))\) alors \(f\) est constante sur chaque \(X_i\text{.}\)

Hint

Commencer par déterminer la tribu-trace \(\mathscr T_i\) de \(\mathscr T\) sur chaque \(X_i\text{,}\) puis utiliser Project 7.1.

Solution

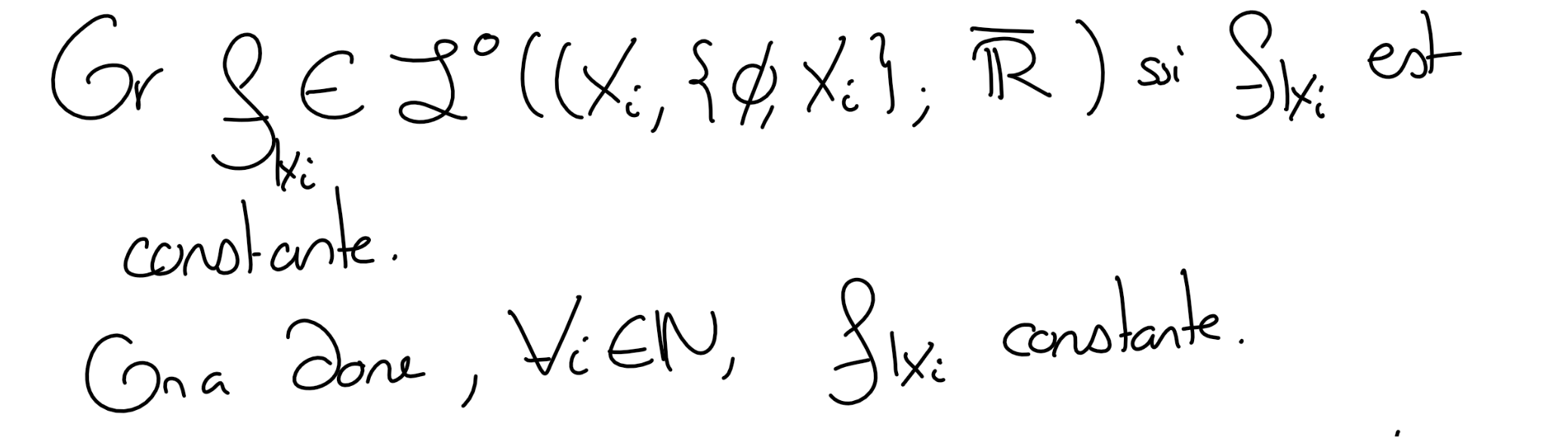
(b)

Réciproquement, montrer que si \(f\) est constante sur chaque \(X_i\) alors \(f\in \mathcal L^0((X,\mathscr T);(\mathbb R,\mathscr B(\mathbb R)))\text{.}\)

Hint

Pour un borélien donné \(B\text{,}\) il s'agit de trouver un sous-ensemble \(J\subset I\) tel que \(f^{-1}(B)=\cup_{j\in J}X_j\text{.}\)

Solution

Remarque: Dans l'exemple précédent, on peut prendre pour espace d'arrivée n'importe quel espace mesurable \((Y,\mathscr S)\) qui contient les singletons.