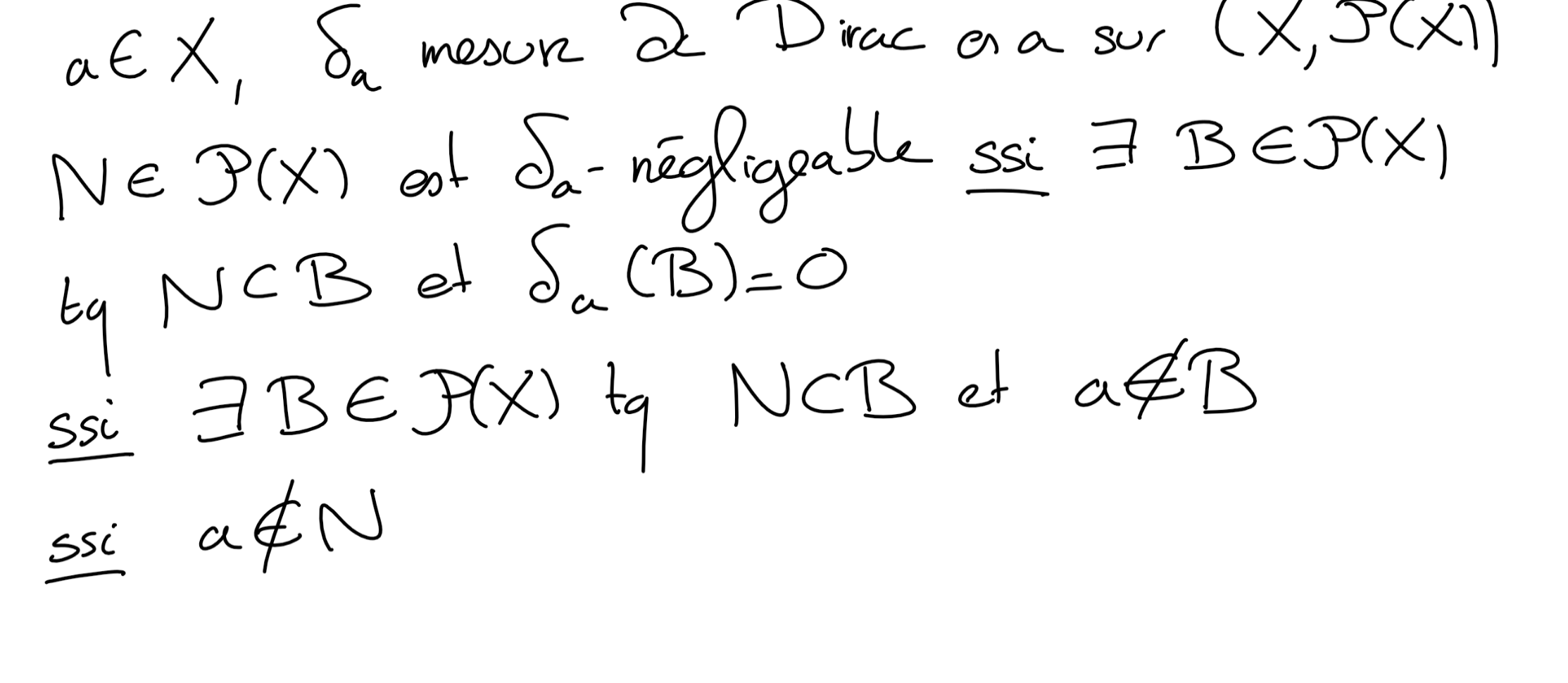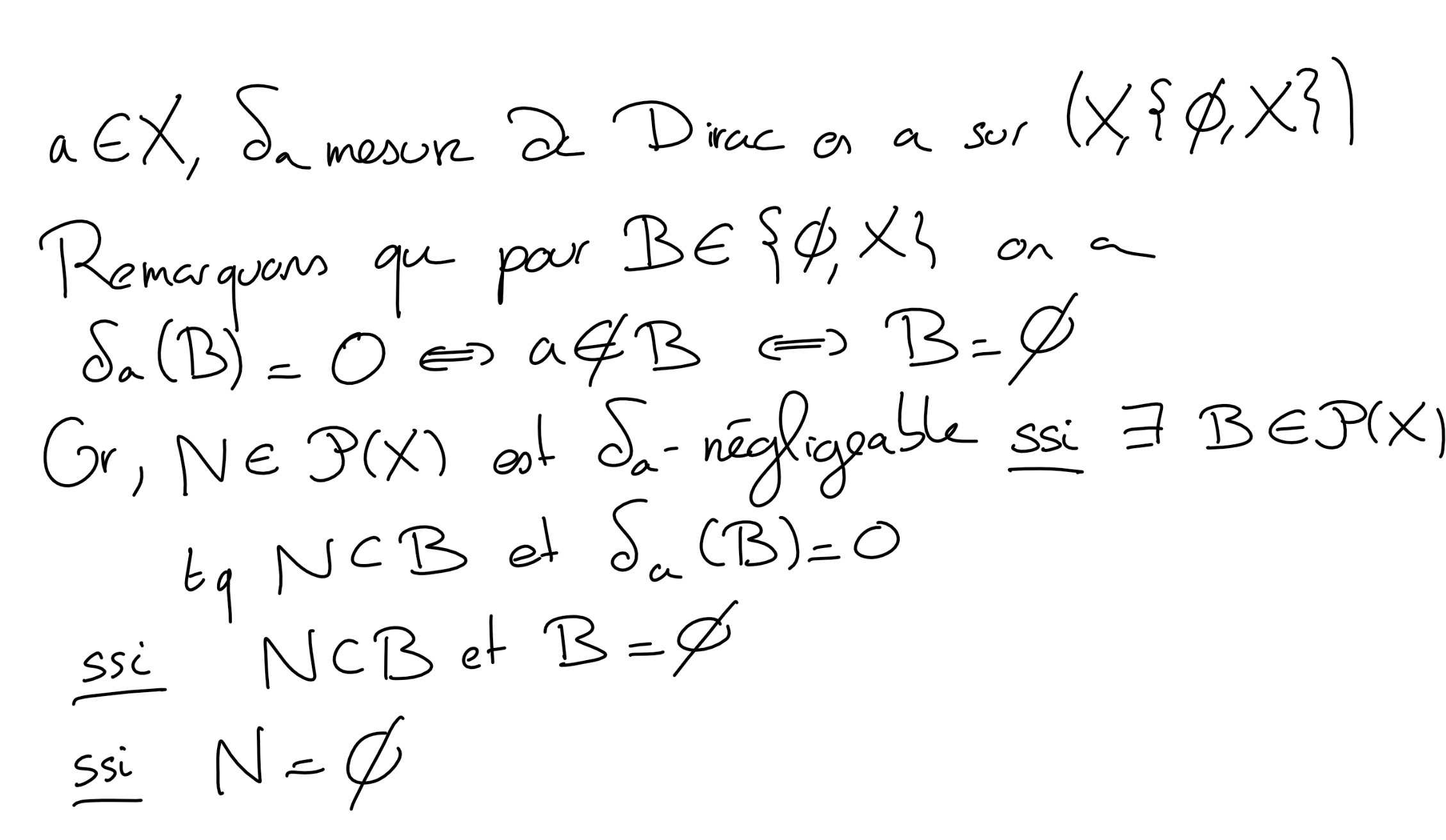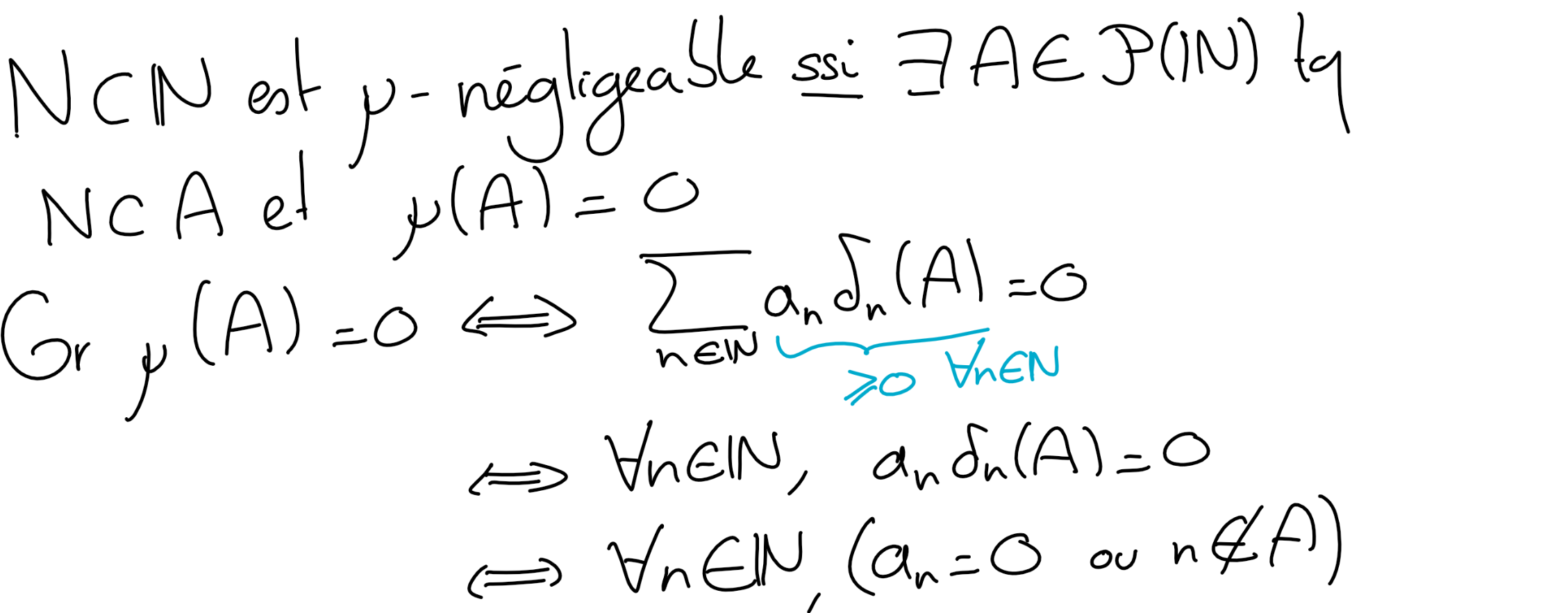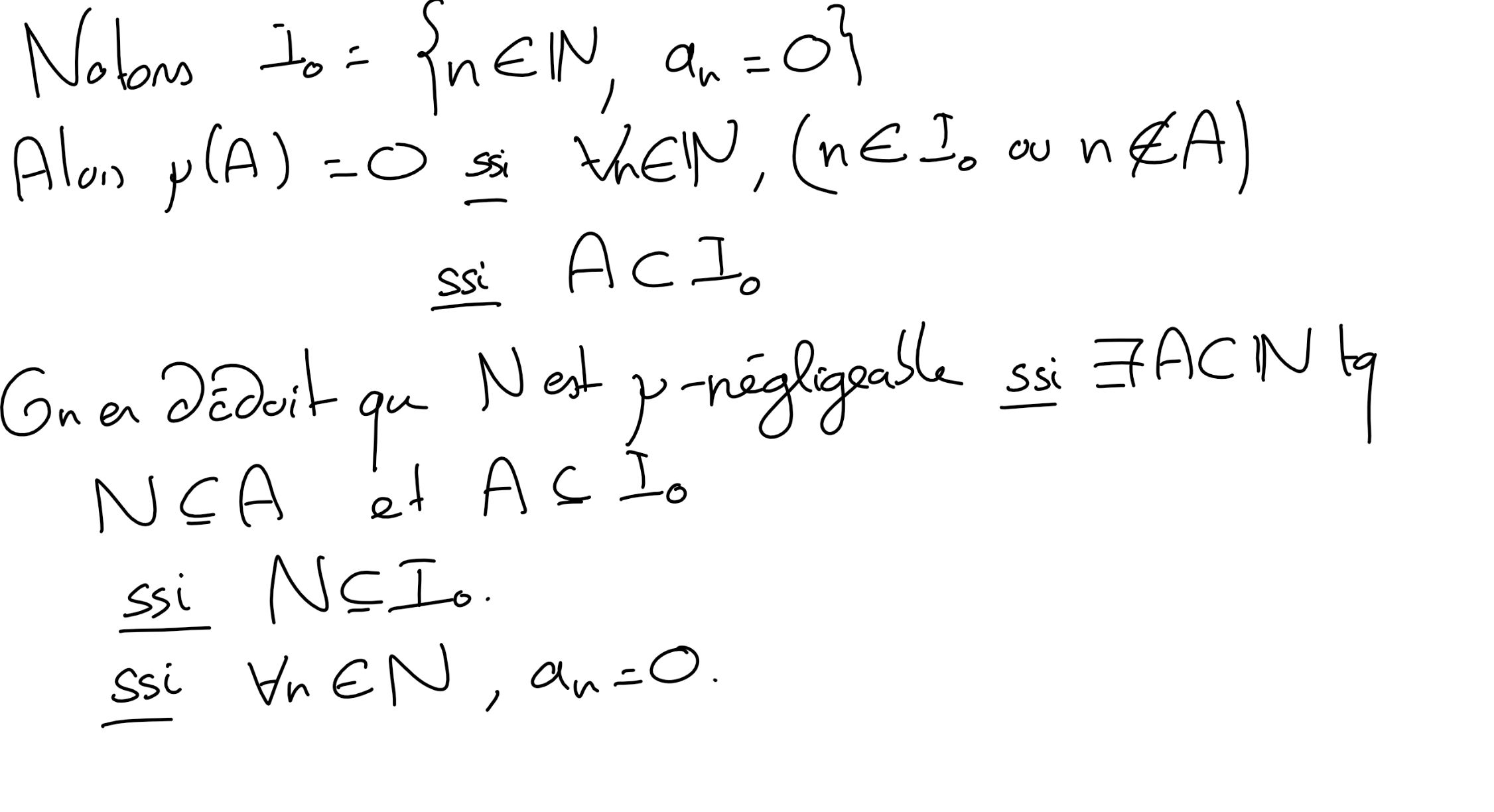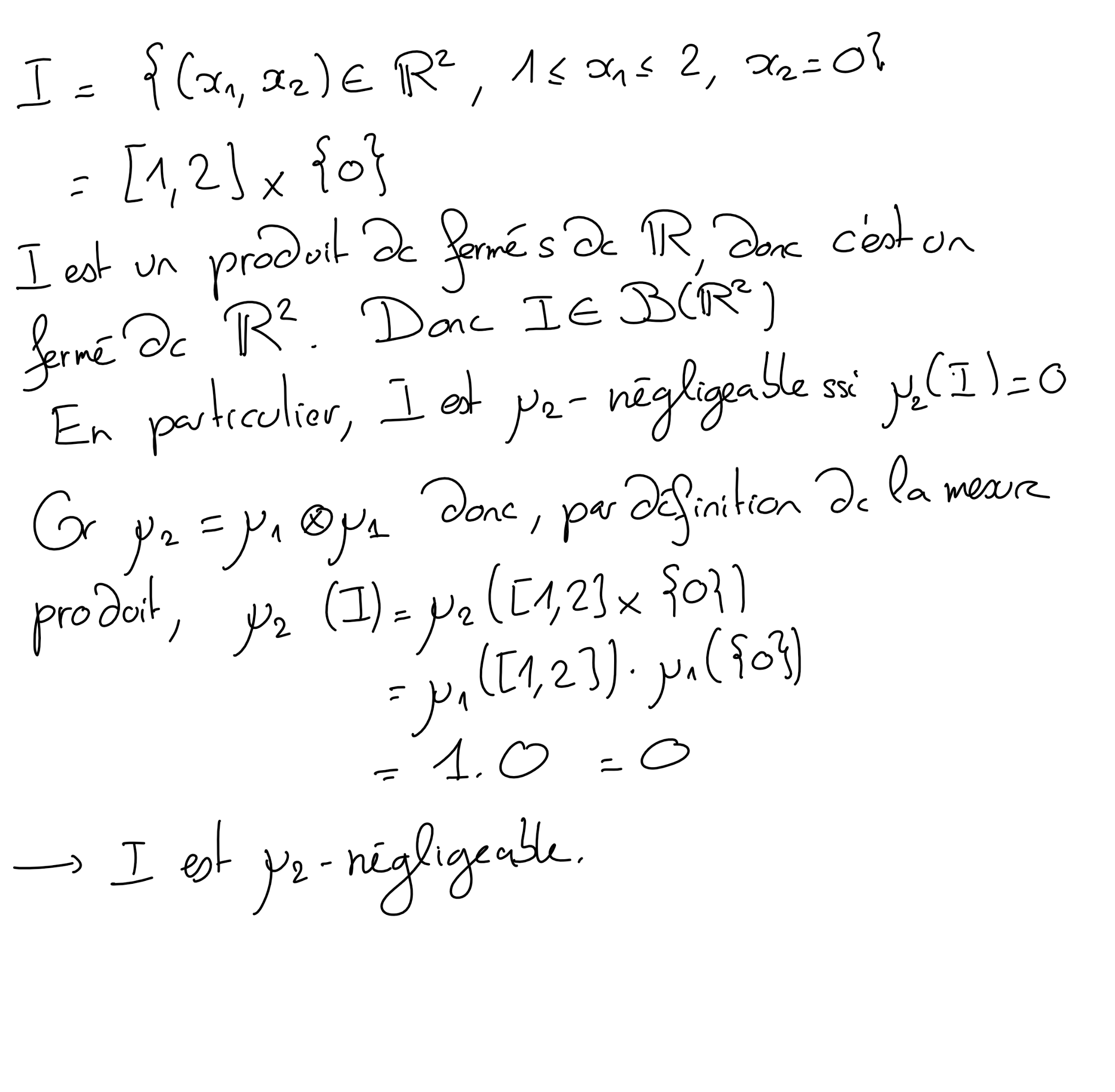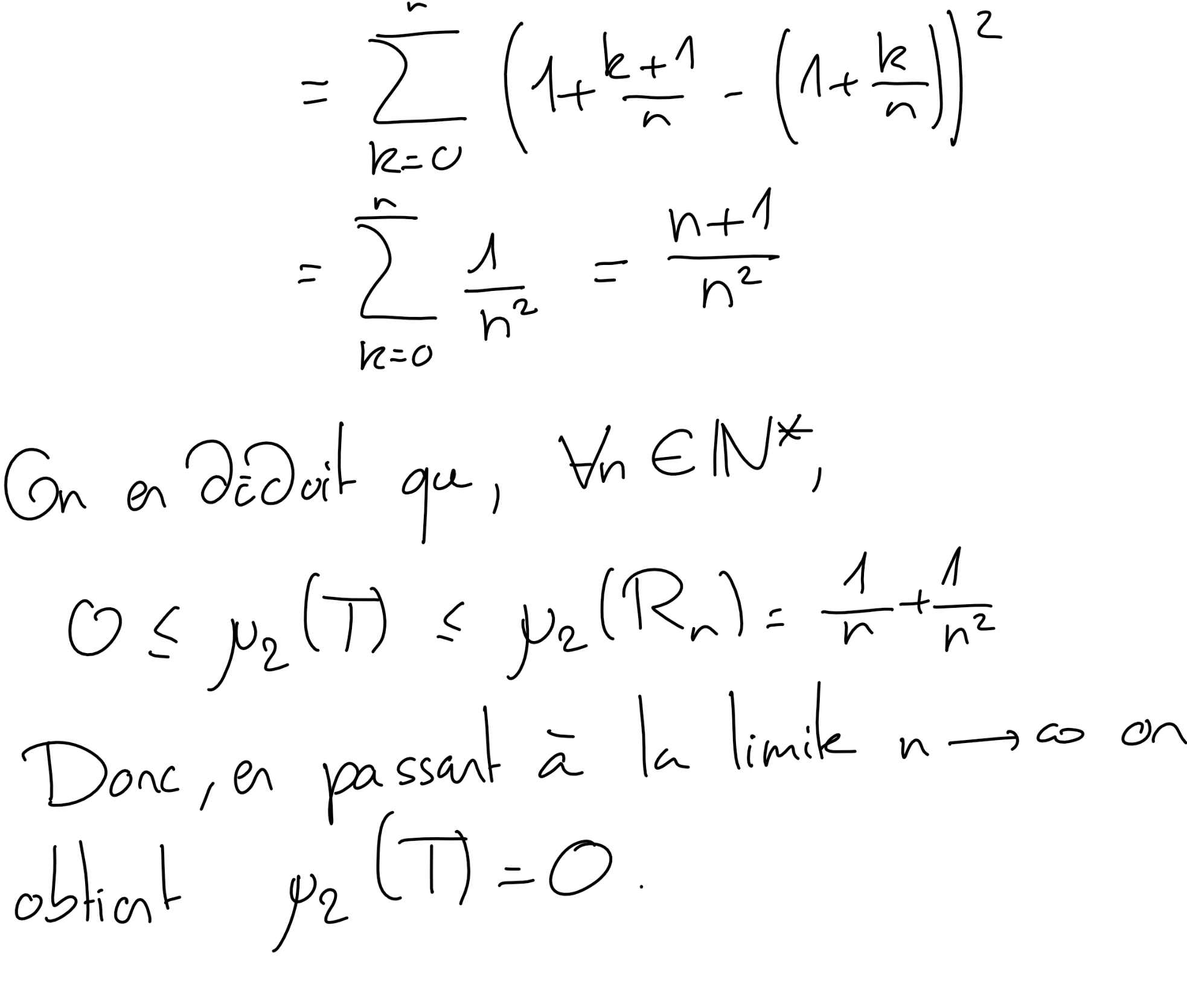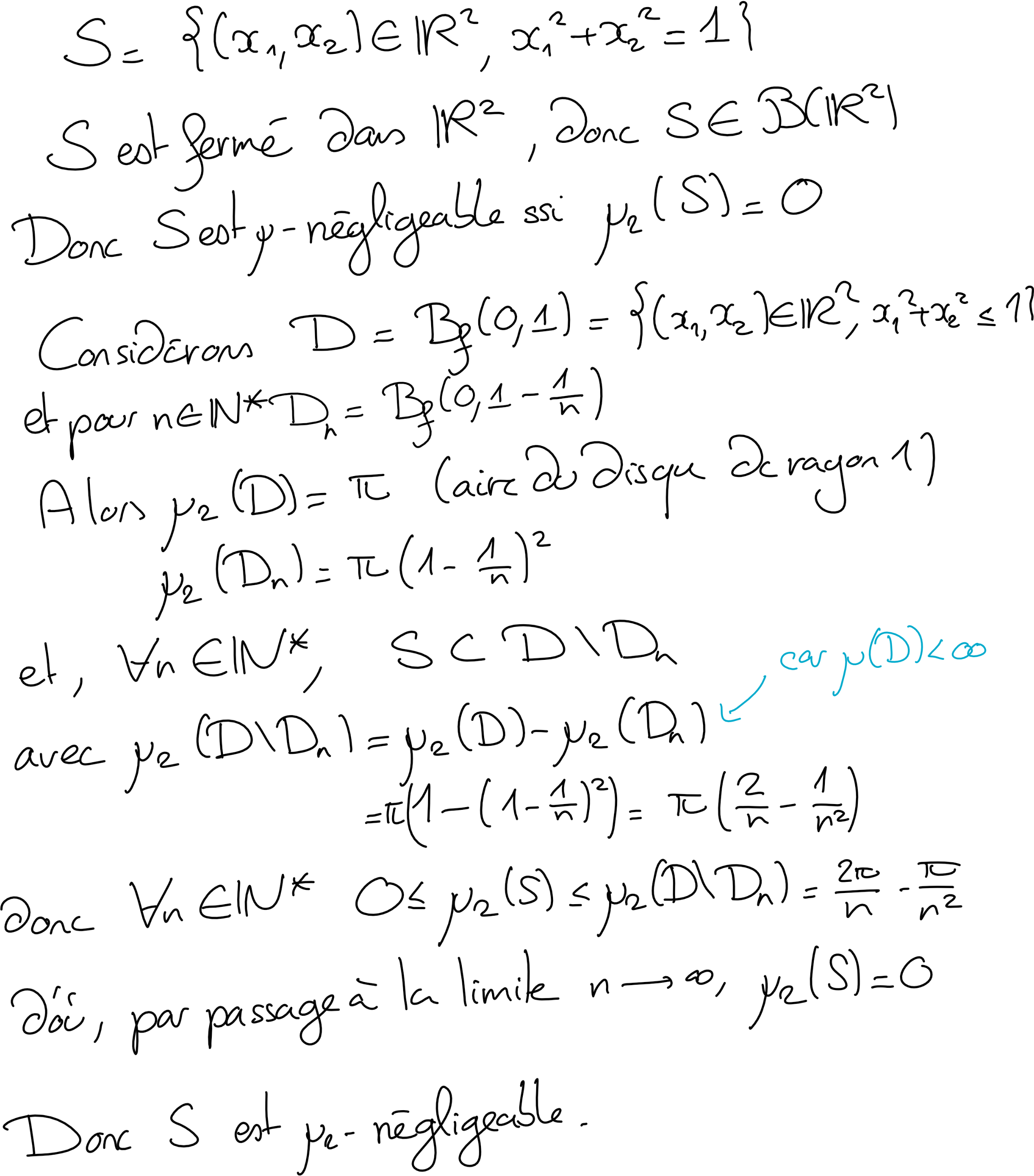Skip to main content

Section 5 Parties négligeables.

Definition 5.1.

Soit \((X,\mathscr T, \mu)\) un espace mesuré, et \(N\in \mathcal P(X)\text{.}\) On dit que \(N\) est \(\mu\)-négligeable s'il existe \(A\in \mathscr T\) tel que \(N\subset A\) et \(\mu(A)=0\text{.}\)

En particulier, si \(N\in \mathscr T\text{,}\) \(N\) est \(\mu\)-négligeable ssi \(\mu(N)=0\text{.}\) Mais les parties négligeables ne sont pas forcément mesurables. Si c'est le cas, autrement dit si, pour tout \(N\in \mathcal P(X),\)

\begin{equation*} N \mu-\text{négligeable } \Rightarrow N \in \mathscr T \end{equation*}

on dit que la tribu \(\mathscr T\) est \(\mu\)-complète (ou que la mesure \(\mu\) est complète.)

On verra que ce n'est pas le cas de la mesure de Borel. Toutefois, il est possible de construire une tribu et une mesure complètes à partir de n'importe quelle mesure: dans le cas de la mesure de Borel, on appelle tribu de Lebesgue la tribu \(\mathscr L(\mathbb R)\) ainsi obtenue, et mesure de Lebesgue la mesure correspondante sur \((\mathbb R, \mathscr L(\mathbb R))\text{.}\)

Project 5.1. Parties \(\delta_a\)-négligeables..
(a)

Soit \(X\) un ensemble, \(a\in A\text{.}\) On considère la mesure de Dirac \(\delta_a\) en \(a\) (introduite à l'Example 2.2). On munit \(X\) de la tribu \(\mathcal P(X)\text{.}\) Déterminer les parties \(\delta_a\)-négligeables de \(X\text{.}\)

Solution
(b)

On munit cette fois \(X\) de la tribu \(\{X,\emptyset\}\text{.}\) Déterminer les parties \(\delta_a\)-négligeables dans ce cas.

Solution

Soit \((a_n)_n \in (\mathbb R_+)^{\mathbb N}\) une suite de réels positifs, on considère la mesure sur \((\mathbb N, \mathcal P(\mathbb N))\) définie par

\begin{equation*} \mu =\sum_{n\in \mathbb N}a_n \delta_n \end{equation*}

Déterminer les parties \(\mu\)-négligeables.

Solution
Project 5.2. Parties négligeables pour la mesure de Borel..
On considère l'espace mesuré \((\mathbb R^2, \mathscr B(\mathbb R^2), \mu_2)\text{,}\) où \(\mu_2=\mu_1 \otimes \mu_1\) est la mesure de Borel sur \(\mathbb R^2\text{.}\)
(a)

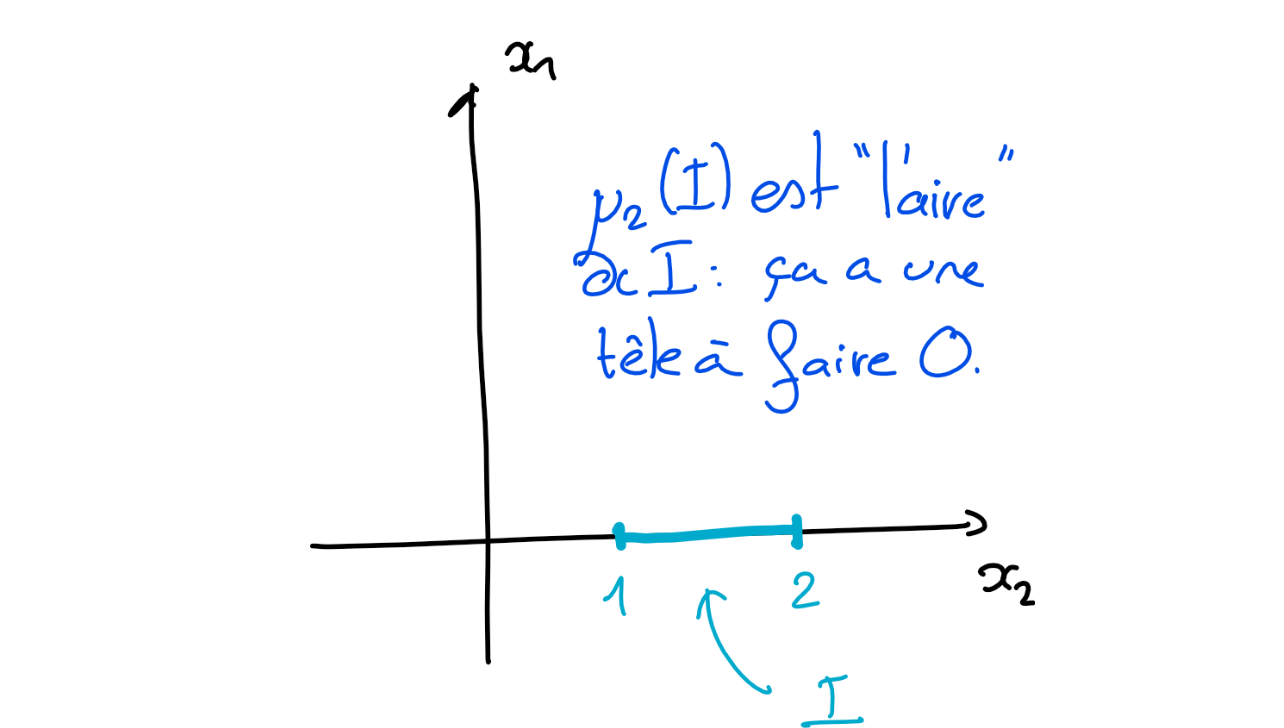
Montrer que l'ensemble

\begin{equation*} I=\{(x_1,x_2)\in \mathbb R^2, 1\leq x_1 \leq 2, x_2=0\} \end{equation*}

est \(\mu_2\)-négligeable.

Hint
Solution
(b)

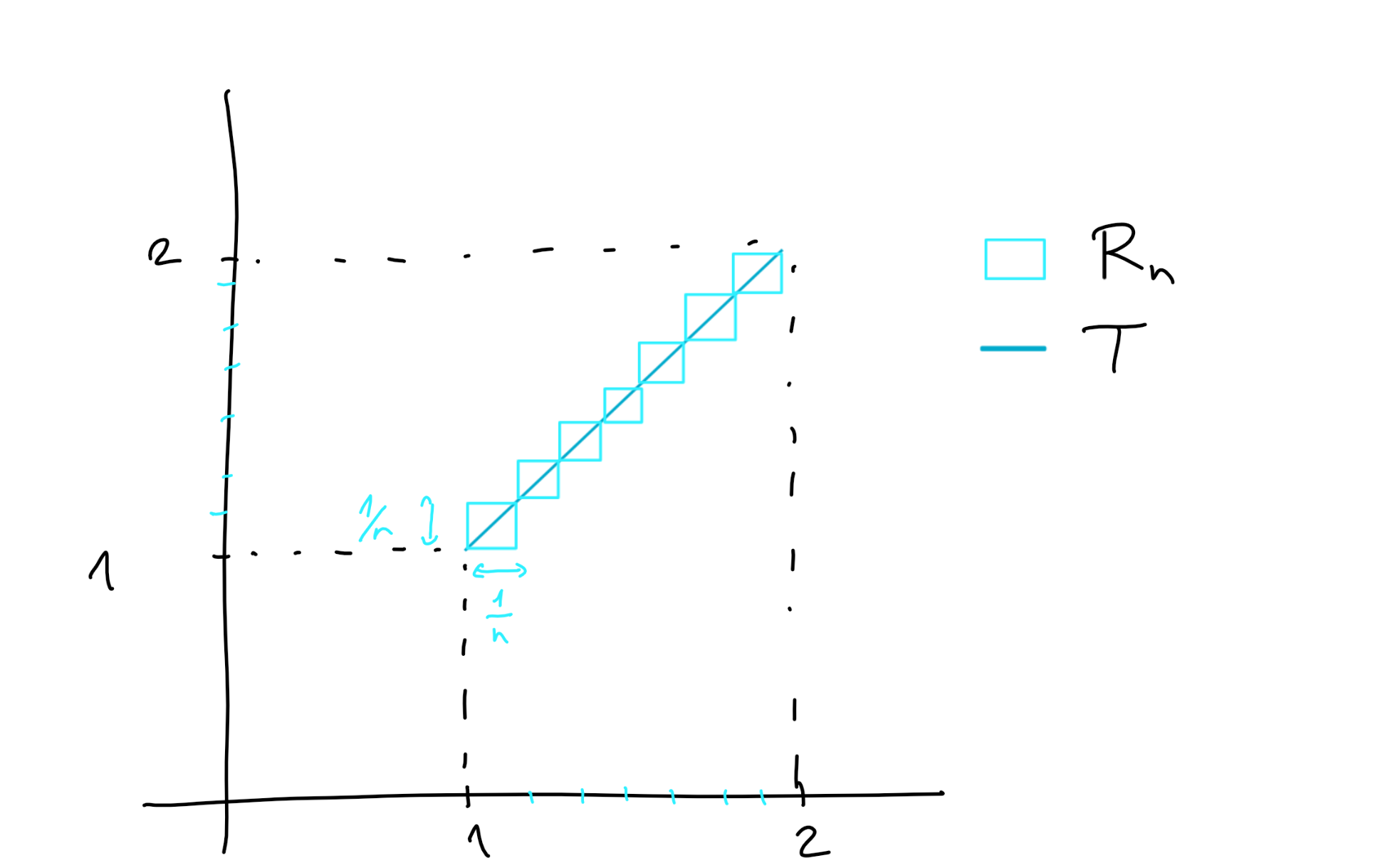
Montrer que le segment reliant \((1,1)\) et \((2,2)\) dans \(\mathbb R^2\text{:}\)

\begin{equation*} T=\{x=(x_1,x_2)\in \mathbb R^2,\ \exists t\in [0,1],\, x=(1-t)\cdot(1,1) + t\cdot(2,2)\} \end{equation*}

est \(\mu_2\)-négligeable.

Hint

L'idée est de "recouvrir" \(T\) avec de petits rectangles (car on sait calculer leur aire, puisque \(\mu_2=\mu_1 \otimes \mu_1\)):

Solution
(c)

Soit \(a\in \mathbb R^2\text{,}\) \(v\in \mathbb R^2\) Montrer que la droite vectorielle passant par \(a\) et dirigée par \(v\text{:}\)

\begin{equation*} D=\{x\in \mathbb R^2,\ \exists t\in \mathbb R,\, xa+tv\} \end{equation*}

est \(\mu_2\)-négligeable.

Hint

On peut commencer par découper \(D\) en segments, puis appliquer un raisonnement similaire à ce qu'on a fait pour \(T\) sur chaque segment:

Solution
(d)

Montrer que le cercle unité:

\begin{equation*} S=\{x=(x_1,x_2)\in \mathbb R^2,\ x_1^2+x_2^2=1\} \end{equation*}

est \(\mu_2\)-négligeable.

On pourra utiliser le fait que si \(D\) est un disque de rayon \(r\text{,}\) l'aire de \(D\) est donnée par \(\mu_2(D)=\pi r^2\text{.}\)

Hint

On peut "coincer" \(S\) entre le disque unité et un disque un tout petit peu plus petit:

Solution