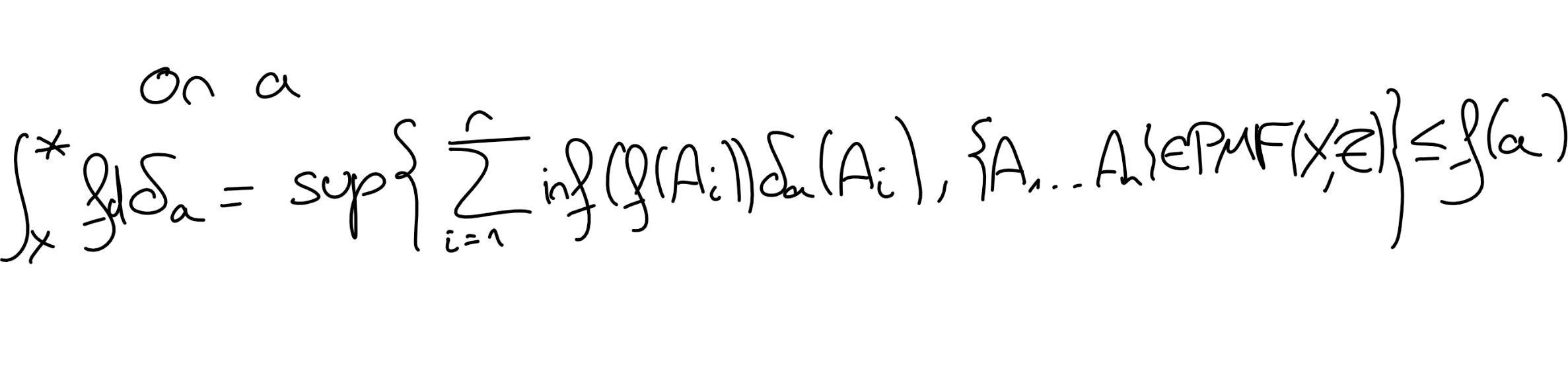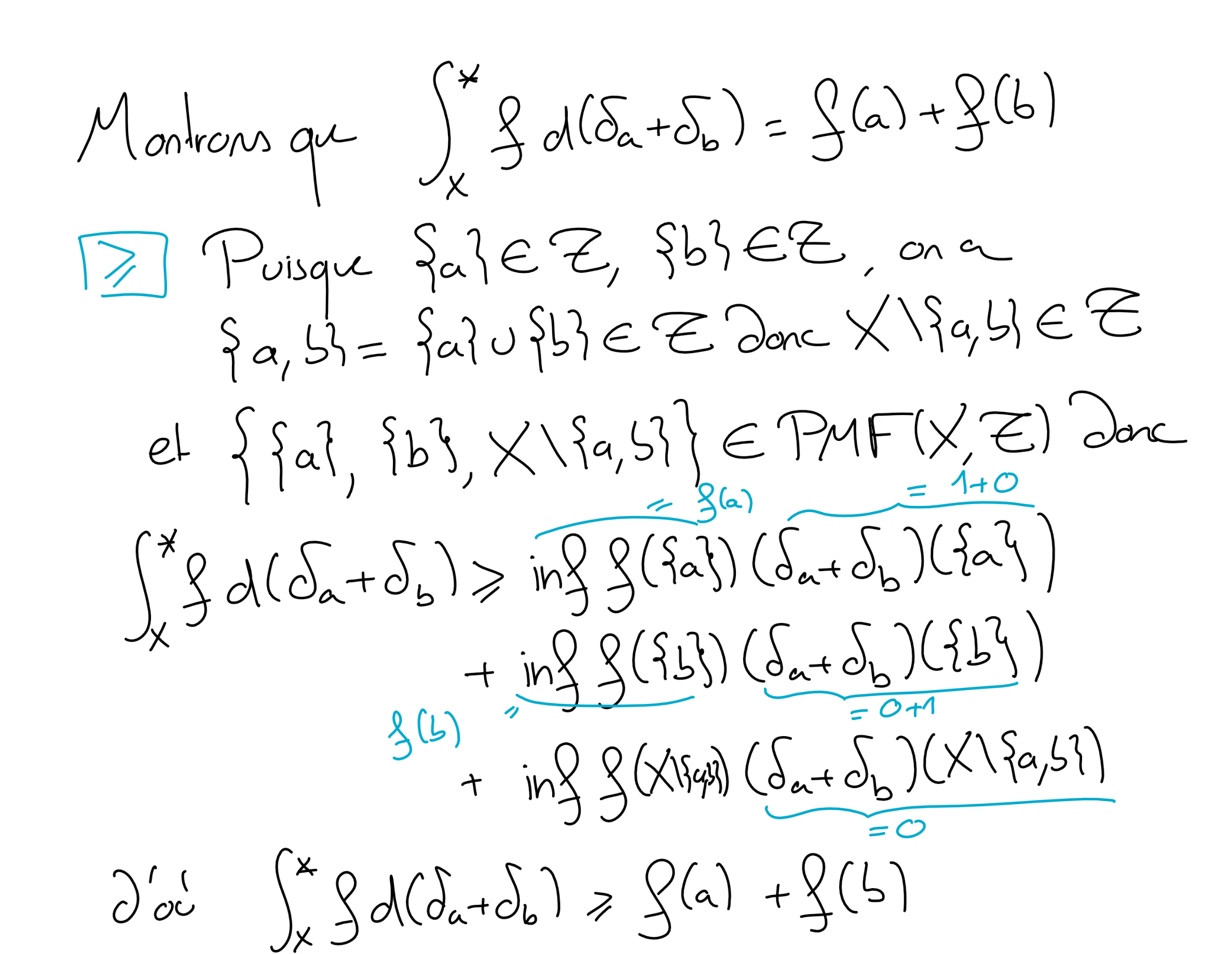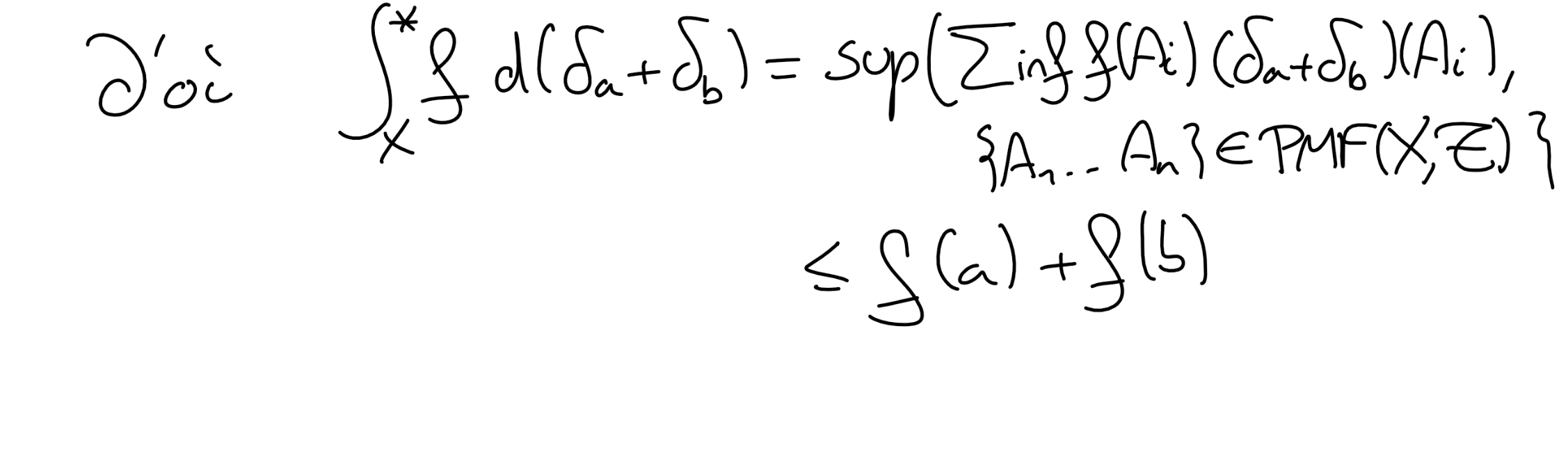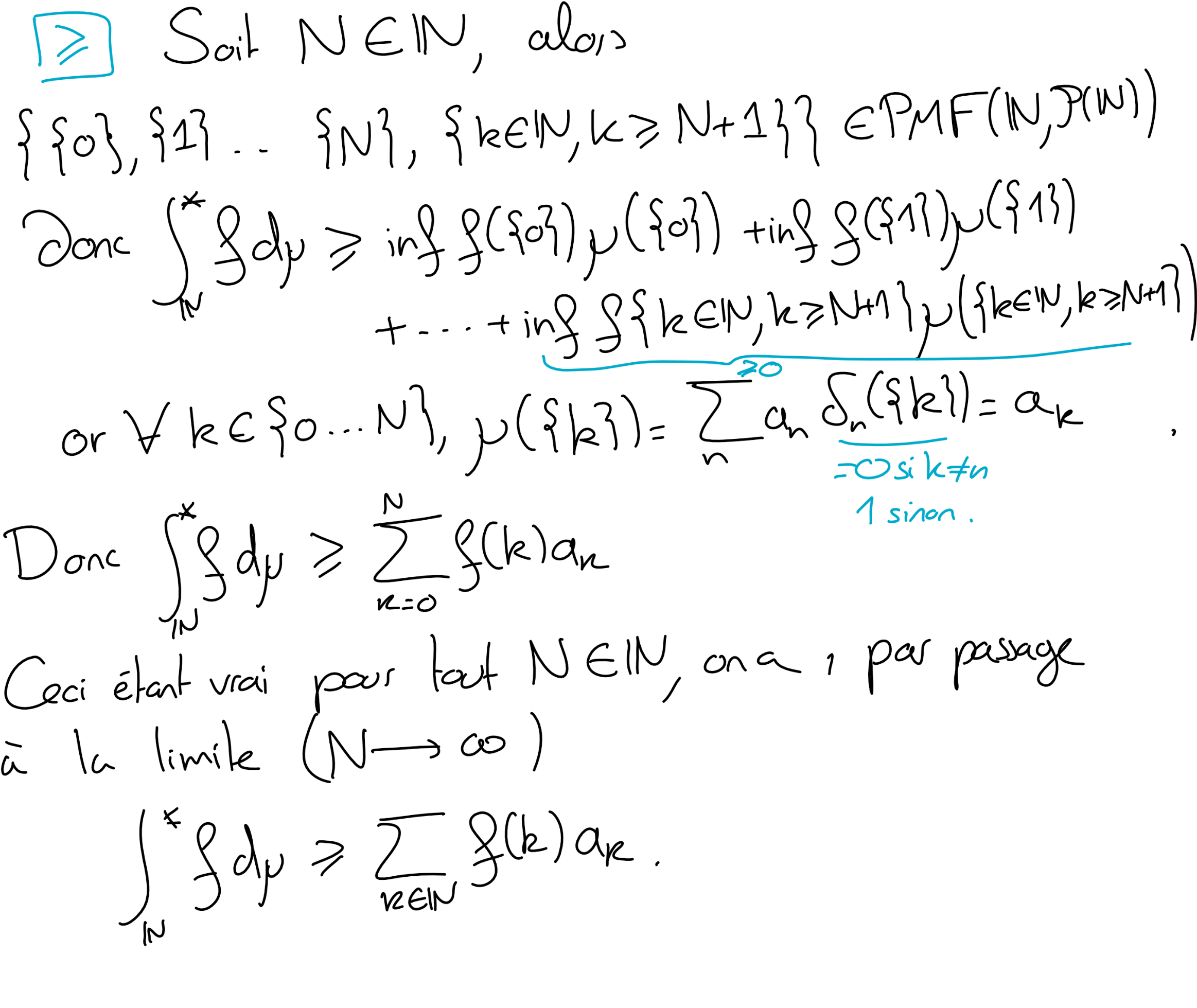Skip to main content

Section 8 Intégrale supérieure

Definition 8.1.

Soit \(\mu\) une mesure sur \((X,\mathscr T)\text{.}\)

  • Soit \(f:(X,\mathscr T)\rightarrow ([0,+\infty], \mathscr B([0,+\infty]))\) une fonction mesurable positive, et \(P=\{A_1,\ldots,A_n\}\) une Partition Mesurable Finie de \((X,\mathscr T)\text{.}\) La somme inférieure de Lebesgue associée est définie par:

    \begin{equation*} \mathscr L(f,P)=\sum_{i=1}^n \inf_{A_i}(f) \mu(A_i). \end{equation*}

  • L'intégrale supérieure de \(f\) par rapport à \(\mu\) est définie par

    \begin{equation*} \int^*_X f d\mu = \sup\{\mathscr L(f,P), P \in PMF(X,\mathscr T)\} \end{equation*}

On en déduit:

  • Pour tout \(A\in \mathscr T\text{,}\) \(\mathbb 1_A\) est mesurable positive, et on a

    \begin{equation*} \int^*_X 1_A d \mu = \mu(A) \end{equation*}

  • Si \(\{B_1,\ldots,B_m\}\) une PMF de \((X,\mathscr T)\) et \((\beta_1, \ldots,\beta_m)\in \mathbb R^m\text{,}\) notons

    \begin{equation*} f = \sum_{k=1}^n \beta_k \mathbb{1}_{B_k} \end{equation*}

    la fonction étagée associée. Alors

    \begin{equation*} \int_X^* f d \mu = \sum_{k=1}^n \beta_k\,\mu(B_k) \end{equation*}
Project 8.1. Intégration par rapport à la masse de Dirac.
(a)

Soit \((X,\mathscr T)\) un ensemble mesurable, \(a\in X\) tel que \(\{a\} \in \mathscr T\text{.}\) On munit \((X,\mathscr T)\) de la mesure de Dirac \(\delta_a\) en \(a\) (voir Example 2.2). Soit \(f\in \mathcal L^0((X,\mathscr T), ([0,+\infty], \mathscr B([0,+\infty])))\text{.}\) Montrer que

\begin{equation*} \int_X^* fd\delta_a = f(a) \end{equation*}
Hint

Procéder par double inégalité: puisque la définition de l'intégrale supérieure fait intervenir un sup, c'est plus pratique.

Solution
(b)

Soit \(b\in X\) un autre point tel que tel que \(\{b\} \in \mathscr T\text{.}\) Montrer que

\begin{equation*} \int_X^* fd(\delta_a+\delta_b) = f(a)+f(b) \end{equation*}
Hint

Pour l'une des inégalités, il peut être utile de considérer une PMF \(\{A_1,\ldots,A_n\}\) de \((X,\mathscr T)\text{,}\) et de séparer les cas selon si \(a\) et \(b\) sont dans le même \(A_{i_0}\) ou dans deux \(A_i\) différents.

Solution
Project 8.2. Intégrales sur \(\mathbb N\).
(a)

Soit \((a_n)_n \in (\mathbb R_+)^{\mathbb N}\) une suite de réels positifs, on considère la mesure sur \((\mathbb N, \mathcal P(\mathbb N))\) définie par

\begin{equation*} \mu =\sum_{n\in \mathbb N}a_n \delta_n. \end{equation*}

Soit \(f\in \mathcal L^0(\mathbb N, \mathcal P(\mathbb N);\overline{\mathbb R}_+)\text{.}\) Montrer que

\begin{equation*} \int_{\mathbb N}^* fd\mu= \sum_{n\in\mathbb N} a_n f(n). \end{equation*}
Solution