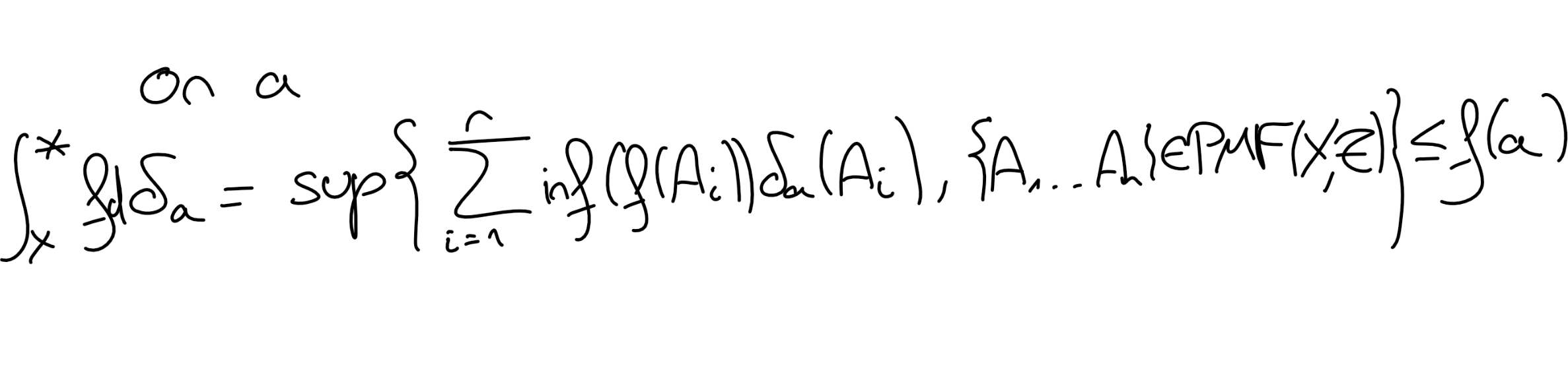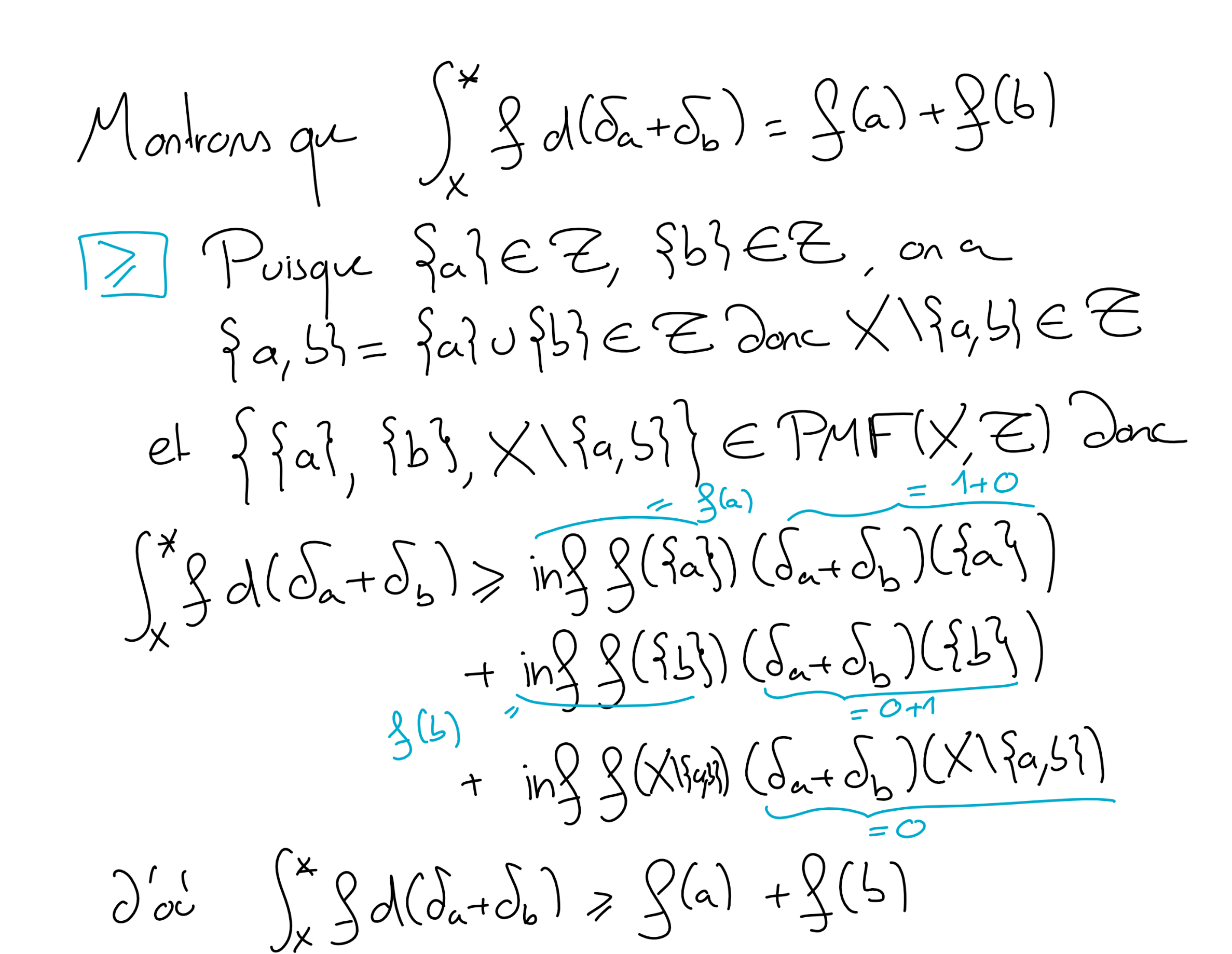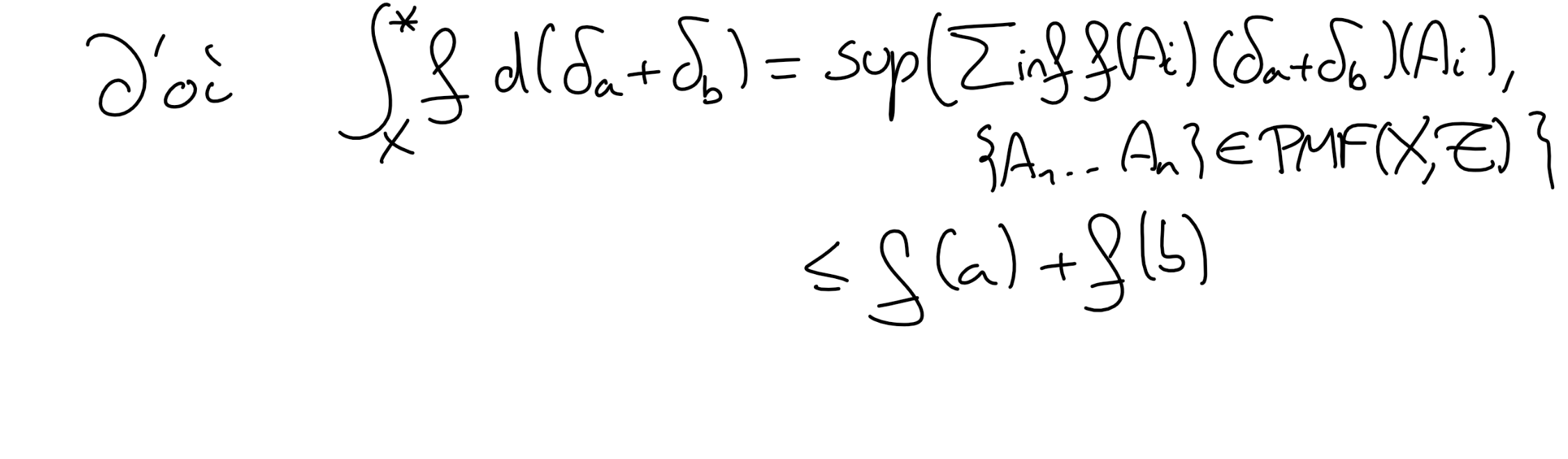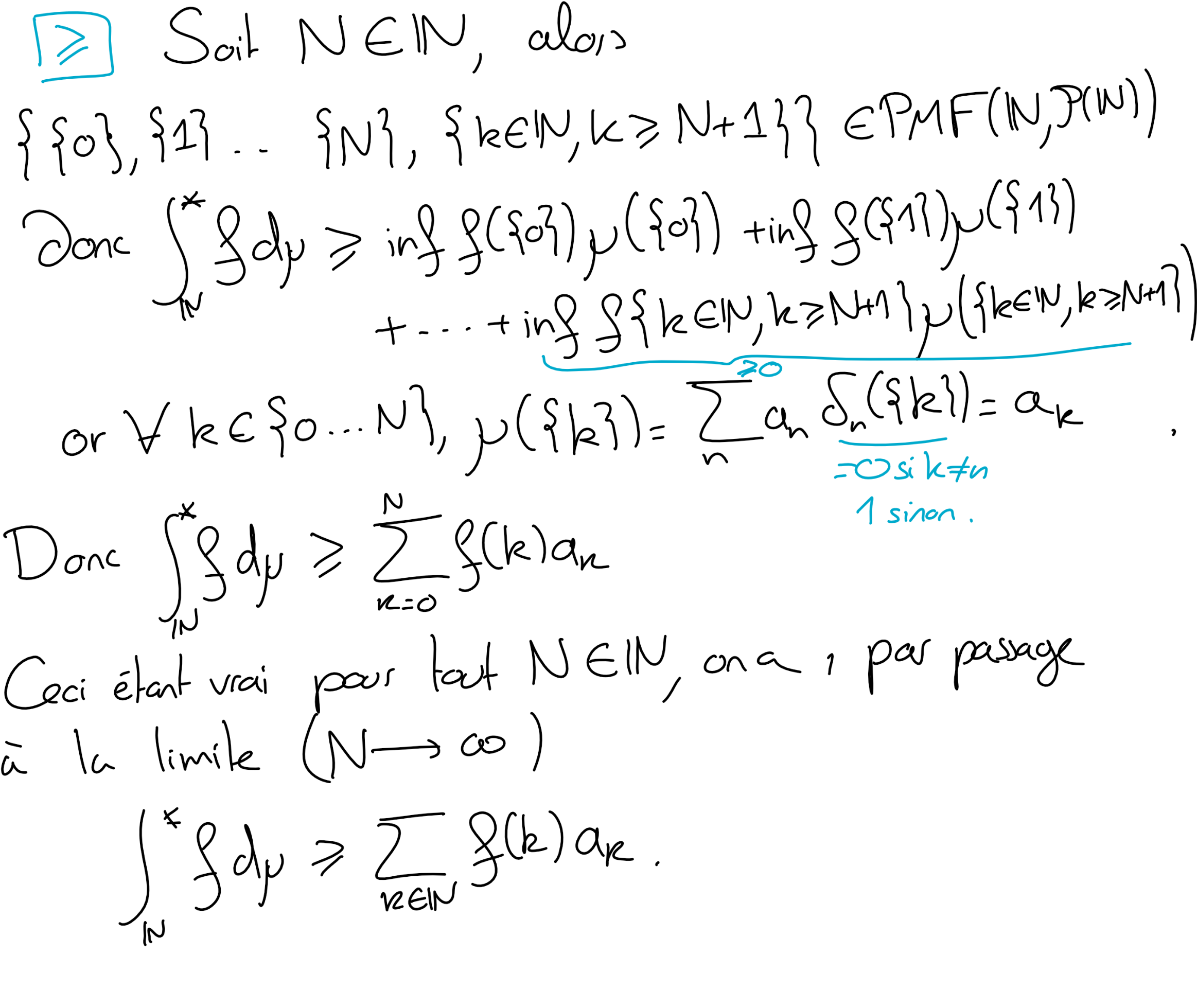Skip to main content

Section 8 Intégrale des fonctions mesurables positives

Définition 8.1.

Soit \(\mu\) une mesure sur \((X,\mathscr T)\text{.}\)

  • Soit \(e : X \rightarrow \R^+\) une fonction étagée positive, et \(P=\{A_1,\ldots,A_n\}\) une partition mesurable finie de \((X,\mathscr T)\) telle que

    \begin{equation*} e=\sum_{k=1}^n \alpha_i 1_{A_i} \end{equation*}

    (avec \(\alpha_i \in\R^+\))

    On définit l'intégrale de \(e\) par rapport à \(\mu\) par:

    \begin{equation*} \int_X e\,d\mu = \sum_{k=1}^n \alpha_i \mu(A_i) \end{equation*}

  • Soit \(f:(X,\mathscr T)\rightarrow (\rbb 0,+\infty\lbb , \mathscr B(\rbb 0,+\infty\lbb ))\) une fonction mesurable positive. On note

    \begin{equation*} \mathcal E(f) = \{e :X\rightarrow\R^+,\, e \text{ étagée },\ \forall\, x\in X,\, 0\leq e(x) \leq f(x) \} \end{equation*}

    l'ensemble des fonctions étagées positives inférieures à \(f\text{.}\)

    Avec ça, on définit l'intégrale de \(f\) par rapport à \(\mu\) par

    \begin{equation*} \int_X f d\mu = \sup\left\{\int_X e\,d\mu, e\in \mathcal E(f)\right\} \end{equation*}

  • On dit que \(f\) est intégrable si

    \begin{equation*} \int_X f d\mu \lt \infty \end{equation*}

    ⚠ Du moment que \(f\) est mesurable positive, l'intégrale de \(f\) existe même si \(f\) n'est pas intégrable: elle est alors égale à \(+\infty\text{.}\)

Exercice 8.1.

Sur l'espace mesurable \((\R,\B(\R))\text{,}\) on définit

\begin{equation*} \mu : B\in \B(\R) \mapsto 5\delta_\pi(A)+3\delta_2(A) \end{equation*}

(a)

Justifier que \(\mu\) est une mesure finie sur \((\R,\B(\R))\text{.}\)

Spoiler.

(b)

Montrer que \(]-\infty,0\,]\) est \(\mu\)-négligeable.

Spoiler.

(c)

Justifier que \(f=\mathbb{1}_{[1,2]}+3\mathbb{1}_{[3,5[}\) est étagée. Calculer \(\displaystyle \int_{\R}f\,d\mu\) et \(\displaystyle\int_{]-\infty,0]}f\,d \mu\text{.}\)

Spoiler.

(d)

Justifier que \(g:x\in\R\mapsto |x|\in\R\) est borélienne. En utilisant la définition de l'intégrale, montrer que \(\displaystyle \int_{\R} g\, d\mu \geq 18\text{.}\)

Spoiler.

Exercice 8.2.

Sur l'espace mesurable \((\R,\B(\R))\text{,}\) on définit

\begin{equation*} \nu : B\in \B(\R) \mapsto \frac12\delta_{1}(A)+2\delta_{3}(A) \end{equation*}

(a)

Justifier que \(\nu\) est une mesure finie sur \((\R,\B(\R))\text{.}\)

Spoiler.

(b)

Montrer que \(]5,+\infty\,[\) est \(\nu\)-négligeable.

Spoiler.

(c)

Justifier que \(f=\mathbb{1}_{[-1,1]}+4\mathbb{1}_{[2,4[}\) est étagée. Calculer \(\displaystyle \int_{\R}f\,d\nu\) et \(\displaystyle\int_{]5,+\infty]}f\,d \nu\text{.}\)

Spoiler.

(d)

Justifier que \(g:x\in\R\mapsto x^2+1\in\R\) est borélienne. En utilisant la définition de l'intégrale, montrer que \(\displaystyle\int_{\R} g\, d\nu \geq \frac{17}2\text{.}\)

Spoiler.

Exercice 8.3.

Soit \(a\in\R\) fixé. On rappelle que la mesure de Dirac en \(a\) est :

\begin{equation*} \delta_a:A \in \mathcal P(\R) \mapsto \begin{cases} 1 \text{ si }a\in A\\ 0 \text{ si }a\notin A \end{cases} \end{equation*}

On définit la mesure \(m\) sur \((\R,\mathcal P(\R))\) par

\begin{equation*} m = \delta_0 + 3\delta_\pi \end{equation*}

But: Montrer que pour toute fonction \(f:\R\rightarrow\R^+\text{,}\)

\begin{equation*} (\star)\quad \int_{\R}^*f\, dm = f(0) + 3f(\pi) \end{equation*}

(a)

Justifier que \(\displaystyle\int^*_\R f\, dm\) existe, quelle que soit la fonction \(f:\R\rightarrow\R^+\text{.}\)

Spoiler.

(b)

Montrer que \((\star)\) est vérifiée pour \(f=1_A\text{,}\) où \(A\subset \R\text{.}\)

Spoiler.

(c)

En déduire que \((\star)\) est vérifiée si \(f=\sum_{k=1}^n \alpha_k 1_{A_k}\text{,}\) où \(A_1,\ldots,A_n\) est une partition de \(\R\) et \(\alpha_1,...,\alpha_n\) sont des réels positifs.

Spoiler.

(d)

Montrer que \((\star)\) est vérifiée pour toute fonction la fonction \(f:\R\rightarrow\R^+\text{.}\)

Spoiler.

(e)

La fonction \(f\) est-elle \(m\)-intégrable ?

Spoiler.

Exercice 8.4.

On définit la mesure \(m\) sur \((\R,\mathcal P(\R))\) par

\begin{equation*} m = \delta_{-1} + \delta_{\sqrt 2} \end{equation*}

On veut montrer que pour toute fonction \(h:\R\rightarrow\R^+\text{,}\)

\begin{equation*} (\star)\quad \int_{\R}^*\, h\, dm = h(-1) + h(\sqrt 2) \end{equation*}

(a)

Justifier que \(\displaystyle\int_\R h\, dm\) existe, quelle que soit la fonction \(h:\R\rightarrow\R^+\text{.}\)

Spoiler.

(b)

Montrer que \((\star)\) est vérifiée pour \(h=1_X\text{,}\) où \(X\subset \R\text{.}\)

Spoiler.

(c)

En déduire que \((\star)\) est vérifiée si \(h=\sum_{k=1}^n y_k 1_{X_k}\text{,}\) où \(X_1,\ldots,X_n\) est une partition de \(\R\) et \(y_1,...,y_n\) sont des réels positifs.

Spoiler.

(d)

Montrer que \((\star)\) est vérifiée pour toute fonction la fonction \(h:\R\rightarrow\R^+\text{.}\)

Spoiler.

(e)

La fonction \(h\) est-elle \(m\)-intégrable ?

Spoiler.

Exercice 8.5. Intégration par rapport à la masse de Dirac.

(a)

Soit \((X,\mathscr T)\) un ensemble mesurable, \(a\in X\) tel que \(\{a\} \in \mathscr T\text{.}\) On munit \((X,\mathscr T)\) de la mesure de Dirac \(\delta_a\) en \(a\) (voir Exercice 2.2). Soit \(f\in \mathcal L^0((X,\mathscr T), (\rbb 0,+\infty\lbb , \mathscr B(\rbb 0,+\infty\lbb )))\text{.}\) Montrer que

\begin{equation*} \int_X^* fd\delta_a = f(a) \end{equation*}
Indice.

Procéder par double inégalité: puisque la définition de l'intégrale supérieure fait intervenir un sup, c'est plus pratique.

Spoiler.

(b)

Soit \(b\in X\) un autre point tel que tel que \(\{b\} \in \mathscr T\text{.}\) Montrer que

\begin{equation*} \int_X^* fd(\delta_a+\delta_b) = f(a)+f(b) \end{equation*}
Indice.

Pour l'une des inégalités, il peut être utile de considérer une PMF \(\{A_1,\ldots,A_n\}\) de \((X,\mathscr T)\text{,}\) et de séparer les cas selon si \(a\) et \(b\) sont dans le même \(A_{i_0}\) ou dans deux \(A_i\) différents.

Spoiler.

Exercice 8.6. Intégrales sur \(\mathbb N\).

(a)

Soit \((a_n)_n \in (\mathbb R_+)^{\mathbb N}\) une suite de réels positifs, on considère la mesure sur \((\mathbb N, \mathcal P(\mathbb N))\) définie par

\begin{equation*} \mu =\sum_{n\in \mathbb N}a_n \delta_n. \end{equation*}

Soit \(f\in \mathcal L^0(\mathbb N, \mathcal P(\mathbb N);\overline{\mathbb R}_+)\text{.}\) Montrer que

\begin{equation*} \int_{\mathbb N}^* fd\mu= \sum_{n\in\mathbb N} a_n f(n). \end{equation*}
Spoiler.