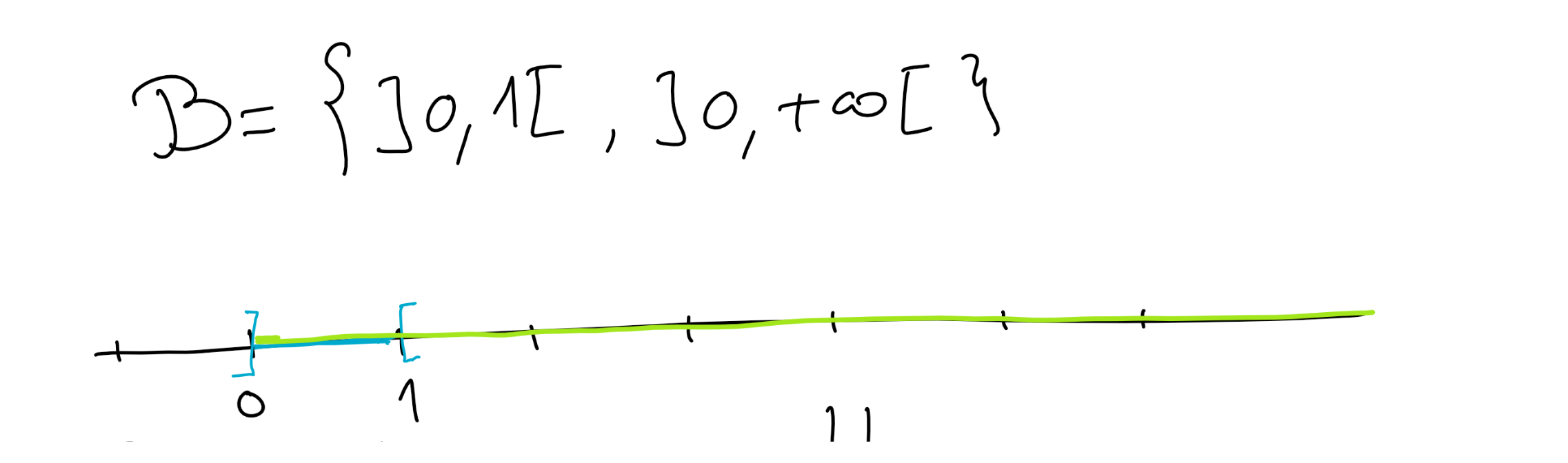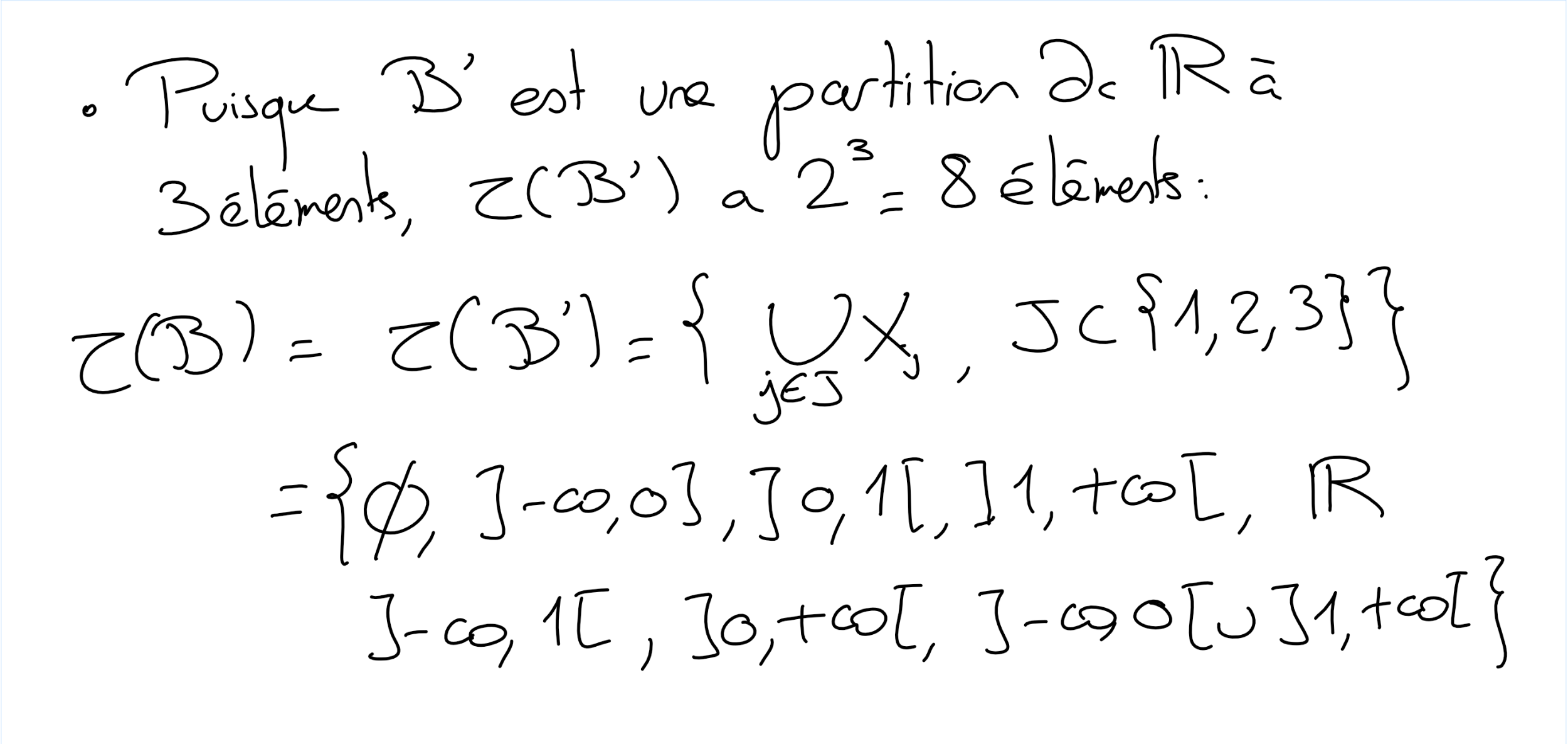Tribus et tribus engendrées

Skip to main content

\(\newcommand{\K}{\mathbb{K}} \newcommand{\Z}{\mathbb{Z}} \renewcommand{\L}{\mathcal L} \newcommand{\B}{\mathscr B} \newcommand{\T}{\mathscr T} \newcommand{\M}{\mathcal M} \newcommand{\P}{\mathcal P} \newcommand{\Q}{\mathbb{Q}} \newcommand{\N}{\mathbb{N}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\lbb}{\,] \,} \newcommand{\rbb}{\,[ \,} \newcommand{\ind}{\mathds{1}} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\rg}{rg} \DeclareMathOperator{\Ker}{Ker} \DeclareMathOperator{\Id}{Id} \DeclareMathOperator{\Image}{Im} \DeclareMathOperator{\Card}{Card} \DeclareMathOperator{\Vect}{Vect} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9} \newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}} \)

Section 1 Tribus et tribus engendrées

Définition 1.1.

Soit \(\Omega\) un ensemble non vide, une tribu de parties de \(\Omega\) est une famille \(\mathscr T \subset \mathcal P(\Omega)\) de sous-ensembles de \(\Omega\) qui vérifie

\(\Omega\in \mathscr T\text{.}\)
Pour tous \(A,B\in\mathscr T\text{,}\) \(A\setminus B \in \mathscr T\text{.}\)
Pour toute famille dénombrable \((A_n)_n\) d'éléments de \(\mathscr T\text{,}\) on a \(\bigcup_n A_n \in \mathscr T\text{.}\)

On dispose des définitions équivalentes suivantes: \(\mathscr T \subset \mathcal P(\Omega)\) est une tribu de parties de \(\Omega\) ssi

\(\Omega\in \mathscr T\text{.}\)
Pour tout \(A\in\mathscr T\text{,}\) \(A^c \in \mathscr T\text{.}\)
Pour toute famille dénombrable \((A_n)_n\) d'éléments de \(\mathscr T\text{,}\) on a \(\bigcup_n A_n \in \mathscr T\text{.}\)

ssi

\(\Omega\in \mathscr T\text{.}\)
Pour tout \(A\in\mathscr T\text{,}\) \(A^c \in \mathscr T\text{.}\)
Pour toute famille dénombrable \((A_n)_n\) d'éléments de \(\mathscr T\text{,}\) on a \(\bigcap_n A_n \in \mathscr T\text{.}\)

Les exemples les plus simples sont les extrêmes: \(\{\emptyset, \Omega\}\) et \(\mathcal P(\Omega)\) sont des tribus¹ sur \(\Omega\text{.}\) Voyons quelques cas moins triviaux :

Exercice Exemples de tribus

1.

Soit \(\Omega\) un ensemble non vide, et \(A\in\mathcal P(\Omega)\) un sous-ensemble de \(\Omega\text{.}\) Montrer que

\begin{equation*} \mathscr T_1=\{\emptyset, A,A^c, \Omega\}\subset \mathcal P(\Omega) \end{equation*}

est une tribu sur \(\Omega\text{.}\)

2.

Soit \(\Omega\) un ensemble non vide. Montrer que l'ensemble

\begin{equation*} \mathscr T_2=\{E\subset \Omega, E \text{ au plus dénombrable ou } E^c \text{ au plus dénombrable }\} \subset\mathcal P(\Omega) \end{equation*}

est une tribu sur \(\Omega\text{.}\)

Rappel: une union dénombrable d'ensembles au plus dénombrable est encore dénombrable. Par ailleurs, par convention, on considère que \(\emptyset\) est un ensemble fini (de cardinal nul).

3.

Montrer que l'ensemble

\begin{equation*} \mathscr T_3=\{A\subset \mathbb R, A=-A\} \subset\mathcal P(\mathbb R) \end{equation*}

des sous-ensembles de \(\mathbb R\) symétriques par rapport à 0 est une tribu sur \(\mathbb R\text{.}\)

4.

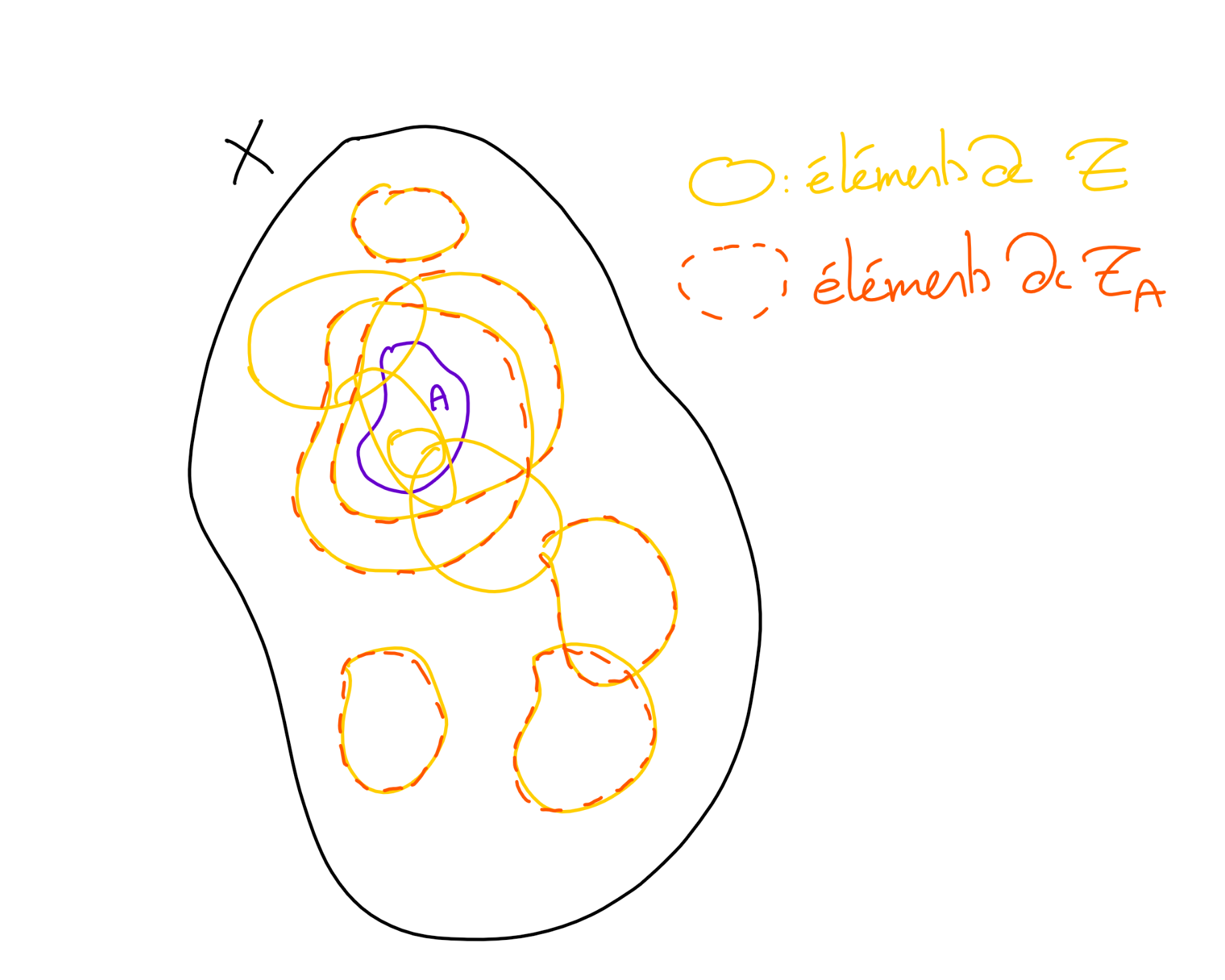
Soit \(\Omega\) un ensemble non vide, et \(\mathscr T\) une tribu sur \(\Omega\text{.}\) Soit de plus \(A\subset \Omega\text{.}\) Montrer que l'ensemble

\begin{equation*} \mathscr T_A=\{B\in \mathscr T, A\subset B \text{ ou } A\cap B = \emptyset\} \subset\mathcal P(\Omega) \end{equation*}

est une tribu sur \(\Omega\text{.}\)

Etant donné une famille \(\mathscr A \subset \mathcal P(\Omega)\) de sous-ensembles de \(\Omega\text{,}\) on peut se demander quelle est la plus petite tribu \(\mathscr T\) sur \(\Omega\) telle que \(\mathscr A \subset \mathscr T\)². On va utiliser le fait suivant:

Si \(\mathscr T, \mathscr T'\) sont deux tribus sur \(\Omega\text{,}\) alors \(\mathscr T\cap\mathscr T'\) est aussi une tribu sur \(\Omega\text{.}\) Plus généralement, si \((\mathscr T_i)_{i\in I}\) est une famille de tribus, alors \(\bigcap_{i\in I}\mathscr T_i\) est aussi une tribu.

Définition 1.2.

Soit \(\mathscr A \subset \mathcal P(\Omega)\text{,}\) on définit la tribu engendrée par \(\mathscr A\) par:

\begin{equation*} \tau(\mathscr A)= \bigcap_{\substack{\mathscr T \text{ tribu} \\ \mathscr A\subset\mathscr T}}\mathscr T \end{equation*}

C'est la plus petite tribu qui contient \(\mathscr A\text{.}\)

Méthode

Pour montrer que \(\tau(\mathscr A)=\mathscr S\text{,}\) on procède par double inclusion:
- \(\boxed{\subset}\) On montre que \(\mathscr S\) est une tribu qui contient \(\mathscr A\text{.}\) Puisque \(\tau(\mathscr A)\) est la plus petite tribu qui contient \(\mathscr A\text{,}\) on a donc \(\tau(\mathscr A)\subset\mathscr S\text{.}\)
- \(\boxed{\supset}\) On montre que toute tribu qui contient \(\mathscr A\) doit aussi contenir \(\mathscr S\) (en général, en utilisant le fait que les éléments de \(\mathscr S\) sont des unions ou intersections dénombrables, ou encore complémentaires, d'éléments de \(\mathscr A\text{.}\) On a alors
  
  \begin{gather*} \forall \mathscr T \text{ tribu t.q. } \mathscr A\subset\mathscr T, \mathscr S\subset\mathscr T\\ \text{ donc } \mathscr S \subset \bigcap_{\substack{\mathscr T \text{ tribu} \\ \mathscr A\subset\mathscr T}}\mathscr T=\tau(\mathscr A) \end{gather*}

Exercice Exemples de tribus engendrées

1.

Montrer que la tribu \(\mathscr T_1\) définie à l'Exercise 1.1 est engendrée par \(\{A\}\subset \mathcal P(\Omega)\text{:}\)

\begin{equation*} \mathscr T_1=\tau(\{A\}). \end{equation*}

2.

Considérons la famille de parties de \(\mathbb Z\) suivante:

\begin{equation*} \mathscr A=\left\{\{n,n+1,n+2\}, n\in \mathbb Z\right\}\subset \mathcal P(\mathbb Z). \end{equation*}

Montrer que

\begin{equation*} \tau(\mathscr A) = P(\mathbb Z) \end{equation*}

Exercice 1.1.

(a)

Montrer que la tribu \(\mathscr T_2\) définie à l'Exercise 1.2 est engendrée par la famille \(\mathscr S\) des singletons de \(\Omega\text{.}\) Autrement dit, soit

\begin{equation*} \mathscr S = \{\{x\}, x\in \Omega\}\subset \mathcal P(\Omega) \end{equation*}

Montrer que

\begin{equation*} \mathscr T_2=\tau(\mathscr S). \end{equation*}

Un singleton est un ensemble au plus dénombrable. Réciproquement, un ensemble fini ou dénombrable \(A\) de \(\Omega\) est une union finie ou dénombrable de singletons:

\begin{equation*} A=\bigcup_{a\in A} \{a\} \end{equation*}

(b)

On suppose que \(\Omega\) a au moins 3 éléments distincts. Considérons maintenant la famille \(\mathscr B\) des sous-ensembles de \(\Omega\) à deux éléments:

\begin{equation*} \mathscr B = \{\{x,y\}, x,y\in \Omega\}\subset \mathcal P(\Omega) \end{equation*}

Montrer que

\begin{equation*} \mathscr T_2=\tau(\mathscr B). \end{equation*}

Utiliser la question précédente: montrer que si \(\{x\}\in\mathscr S\) alors \(\{x\}\in \tau(\mathscr B)\) (en l'écrivant comme intersection d'éléments de \(\mathscr B\text{:}\) c'est là qu'il va être utile d'avoir au moins trois éléments différents).

(c)

Allons plus loin. On maintenant suppose que \(\Omega\) est infini. et on considère la famille \(\mathscr B_n\) des sous-ensembles de \(\Omega\) à \(n\) éléments:

\begin{equation*} \mathscr B_n = \{\{x_1,\ldots,x_n\}, x_i\in \Omega\}\subset \mathcal P(\Omega) \end{equation*}

Montrer que

\begin{equation*} \forall n\in \mathbb N^*,\ \mathscr T_2=\tau(\mathscr B_n). \end{equation*}

Utiliser la méthode de la question précédente pour faire marcher un raisonnement par récurrence.

Exercice 1.2. Tribu engendrée par une partition.

(a)

Montrer que

\begin{equation*} \mathscr T = \{\emptyset, \rbb 0,1\rbb , \lbb -\infty,0\rbb \cup \rbb 1,+\infty\rbb ,\R\} \end{equation*}

est une tribu de parties de \(\R\text{.}\)

Montrer que la tribu engendrée \(\tau({\rbb 0,1\lbb})\) est incluse dans \(\mathscr T\text{.}\)

(b)

Montrer que la famille de parties de \(\mathbb R\) définie par:

\begin{equation*} \mathscr T = \left\{\bigcup_{n\in I} \rbb n,n+1\rbb ,\ I\subset \mathbb Z \right\}\subset \mathcal P(\mathbb R) \end{equation*}

est une tribu de parties de \(\mathbb R\text{.}\)

(c)

Plus généralement, soit \(\Omega\) un ensemble non vide. On considère une partition au plus dénombrable \((\Omega_i)_{i\in I}\) de \(\Omega\text{,}\) autrement dit, \((\Omega_i)_{i\in I}\) est une famille de parties de \(\Omega\) telle que

\begin{equation*} \begin{cases} I \text{ est fini ou dénombrable,}\\ \forall\, i,j\in I \text{ t.q. } i\neq j,\ \Omega_i\cap \Omega_j=\emptyset\\ \Omega=\bigcup_{i\in I}\Omega_i. \end{cases} \end{equation*}

(On suppose de plus, quitte à élaguer, que les \(\Omega_i\) sont non vides)

On définit:

\begin{equation} \mathscr T = \left\{\bigcup_{j\in J}\Omega_j,\ J\subset I\right\}\subset \mathcal P(\Omega)\tag{1.1} \end{equation}

Montrer que \(\mathscr T\) est une tribu sur \(\Omega\text{.}\)

Ca va ressembler furieusement à la question précédente.

(d)

Montrer qu'alors la tribu \(\mathscr T\) définie en (1.1) est engendrée par les ensembles de la partition:

\begin{equation*} \mathscr T = \tau\left(\{\Omega_i,\ i\in I\}\right) \end{equation*}

(e)

Supposons que \(I\) est fini. Combien d'éléments y a-t-il dans la tribu \(\mathscr T\) ?

Combien y a-t-il de sous ensembles \(J\in I\) ?

Considérons l'application:

\begin{align*} \Psi: \mathcal P(I) \amp\rightarrow \mathscr T \\ J\amp \mapsto \bigcup_{j\in J}\Omega_j \end{align*}

Montrons qu'elle est bijective.

\(\Psi\) est surjective par définition de \(\mathscr T\text{:}\) pour tout \(A\in\mathscr T\text{,}\) il existe un sous-ensemble \(J\subset I\) tel que \(A= \cup_{j\in J}\Omega_j\text{.}\)
\(\Psi\) est injective: si \(J\neq J'\) sont deux sous-ensembles distincts de \(I\text{.}\) Alors soit \(J\setminus J' \neq \emptyset\text{,}\) soit \(J' \setminus J \neq \emptyset\text{.}\) Disons \(J\setminus J' \neq \emptyset\) (l'autre cas est symétrique). Soit donc \(j_0\in J\setminus J'\) et \(x\in \Omega_{j_0}\text{.}\) Alors, puisque les \(\Omega_i,\ i\in I\) sont disjoints, pour tout \(i\neq j_0\text{,}\) \(x\notin \Omega_i\text{.}\) En particulier:

\begin{equation*} x\in \bigcup_{j\in J}\Omega_j=\Psi(J) \text{ et } x\notin \bigcup_{j\in J'}\Omega_j=\Psi(J') \end{equation*}

donc \(\Psi(J)\neq \Psi(J')\text{.}\) Donc \(\Psi\) est injective.

Puisque \(\Psi\) réalise une bijection entre \(\mathcal P(I)\) et \(\mathscr T\text{,}\) ces deux ensembles ont le même cardinal, d'où

\begin{equation*} \text{Card}(\mathscr T) = 2^{\text{Card}(I)}. \end{equation*}

(f)

Un exemple: Dans \(\R\text{,}\) posons

\begin{equation*} A_1 = \,]\, - \infty,1\,[\,,\ A_2 = \,[\,1,2\,[\,,\ A_3= \,[\,2,+\infty\,] \end{equation*}

On note \(\mathcal A=\tau(\{A_1,A_2,A_3\})\) la tribu engendrée par la partition \(\{A_1,A_2,A_3\}\text{.}\)

Montrer que \(\mathcal A \subset \B(\R)\text{.}\)

(g)

Quels sont les éléments de \(\mathcal A\) ?

(h)

On note \(\mathscr T = \{[0,4] \cap A, A\in\mathcal A\}\text{.}\) Montrer que \(\mathscr T\) est une tribu sur \([0,4]\text{.}\)

(i)

On peut utiliser cette idée pour déterminer des tribus engendrées plus facilement, en se ramenant à une partition finie.

Dans cet ordre d'idées, déterminer la tribu sur \(\mathbb R\) engendrée par la famille

\begin{equation*} \mathscr A = \{\rbb 0,2\lbb , \rbb 1,3\lbb \}\text{.} \end{equation*}

Trouver une partition \(\mathscr A'=\{\Omega_i, i\in I\}\) de \(\mathbb R\) telle que les \(\Omega_i\) sont dans \(\tau(\mathscr A)\text{:}\) par exemple, des intersections ou complémentaires d'éléments de \(\mathscr A\text{.}\) Puis utiliser les questions précédentes qui décrivent \(\tau(\mathscr A')\text{.}\)

(j)

Toujours suivant cette ligne de raisonnement, déterminer la tribu sur \(\mathbb R\) engendrée par la famille

\begin{equation*} \mathscr B = \{\lbb 0,1\rbb , \lbb 0,+\infty\rbb \}\text{.} \end{equation*}

Même topo: on peut chercher une partition finie \(\mathscr B'\) de \(\mathbb R\) obtenue via des intersections/complémentaires/union d'éléments de \(\mathscr B\text{.}\) Puis utiliser les questions précédentes qui décrivent \(\tau(\mathscr B')\text{.}\)

(k)

Plus généralement, soit \(\Omega\neq \emptyset\) et soient \(A,B \in \mathcal P(\Omega)\) tels que \(A\subset B\text{.}\) Déterminer \(\tau(\{A,B\})\text{.}\)

C'était la situation à l'exemple précédent. Comment généraliser la partition qu'on a utilisée ?

Respectivement, la plus petite et la plus grande

C'est un peu la même idée que de chercher le sous-espace vectoriel engendré par une certaine famille de vecteurs