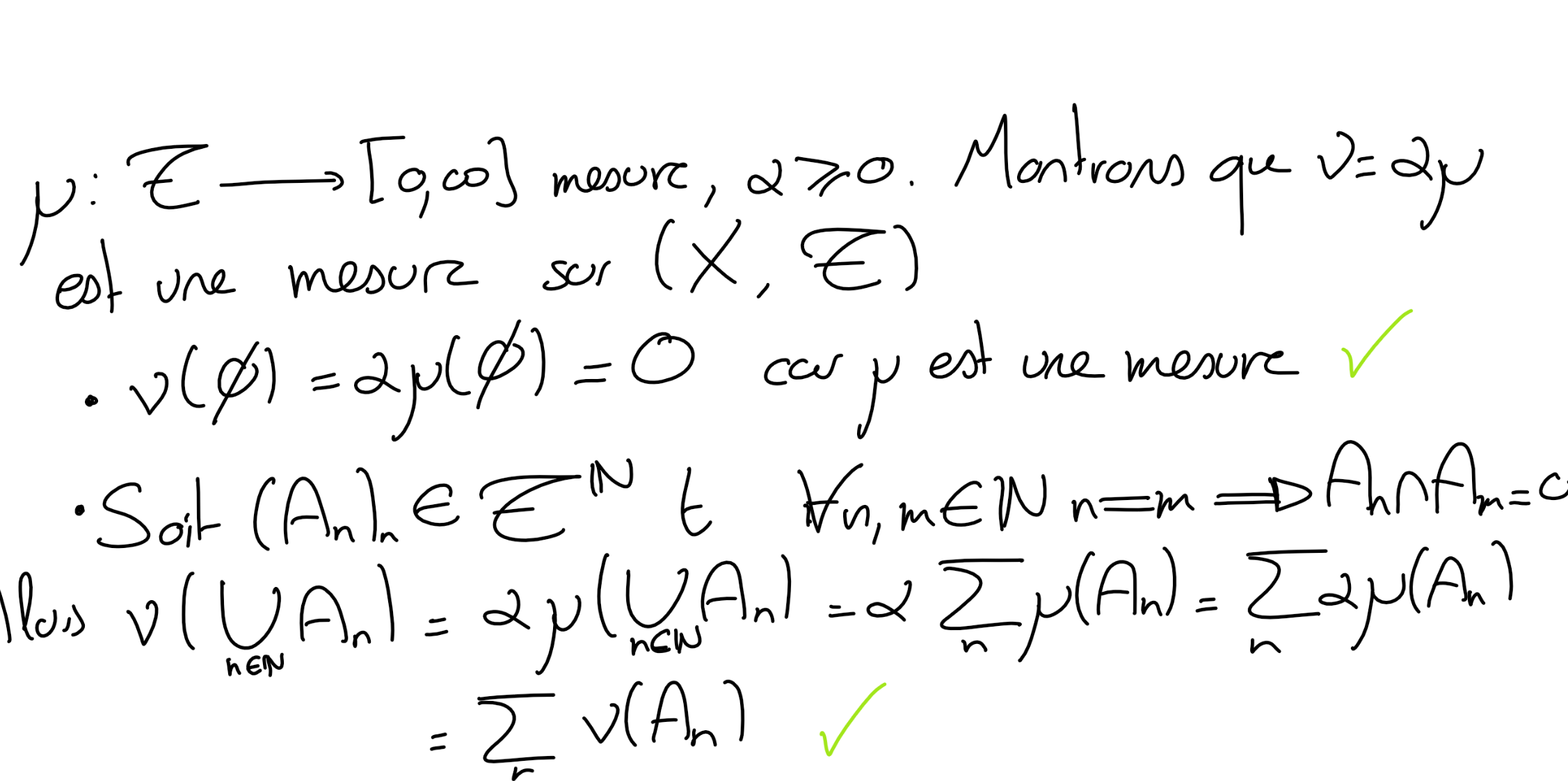Mesures positives.

Section 2 Mesures positives.

Définition 2.1.

Soit \((\Omega,\mathscr T)\) un espace mesurable; autrement dit, \(\mathscr T\) est une tribu sur \(\Omega\text{.}\) Une mesure sur \((\Omega,\mathscr T)\) est une fonction

\begin{equation*} \mu: \mathscr T \rightarrow \rbb 0,+\infty\lbb \end{equation*}

qui vérifie les propriétés suivantes:

\(\displaystyle \mu(\emptyset)=0\)
\(\mu\) est \(\sigma\)-additive: autrement dit, pour toute famille \((A_n)_n \in \mathscr T^{\mathbb N}\) dénombrable disjointe de \(\mathscr T\text{,}\) on a

\begin{equation*} \mu\left(\bigcup_{n\in \mathbb N} A_n\right)=\sum_{n\in \mathbb N} \mu(A_n) \end{equation*}

On dit alors que \((\Omega,\mathscr T, \mu)\) est un espace mesuré.

Un peu de vocabulaire: Soit \((\Omega,\mathscr T, \mu)\) un espace mesuré.

On dit que \(\mu\) est une mesure finie si \(\mu(\Omega)\lt\infty\text{.}\)
On dit que \(\mu\) est une probabilité si \(\mu(\Omega)=1\text{.}\)

Dans ce cas, on la note souvent \(\mathbb P\) plutôt que \(\mu\text{.}\)
On dit que \(\mu\) est une \(\sigma\)-finie s'il existe \((A_n)_n \in \mathscr T^{\mathbb N}\) telle que \(\Omega=\cup_n A_n\) et, pour tout \(n\in \mathbb N,\ \mu(A_n)\lt\infty\text{.}\)

Exercice 2.1. Dépendance à la tribu sur \(\Omega\text{:}\).

Pour tout \(A\subset \N\text{,}\) on pose

\begin{equation*} \nu(A) = \begin{cases} 0 \text{ si } A=\emptyset \\ 1 \text{ si } A\neq \emptyset \end{cases} \end{equation*}

(a)

Considérons la tribu \(\mathscr T_1 = \mathcal P(\N)\text{.}\)

Est-ce que \(\nu\) définit une mesure sur l'espace mesurable \((\N,\mathscr T_1)\) ?

Spoiler.

(b)

Considérons maintenant \(\mathscr T_2 = \{\emptyset, \N\}\text{.}\)

Est-ce que \(\nu\) définit une mesure sur l'espace mesurable \((\N,\mathscr T_2)\) ?

Spoiler.

Exercice 2.2. La mesure de Dirac.

(a)

Soit \(\Omega\) un ensemble, \(a\in \Omega\text{,}\) montrer que l'application

\begin{align*} \delta_a: \mathcal P(\Omega) \amp \rightarrow \rbb 0,+\infty\lbb \\ A \amp \mapsto \begin{cases} 0 \text{ si } a\notin A\\ 1 \text{ si } a \in A \end{cases} \end{align*}

est une mesure sur \((\Omega,\mathcal P(\Omega))\text{.}\) On l'appelle mesure de Dirac en a.

(b)

Montrer que c'est une probabilité sur \((\Omega,\mathcal P(\Omega))\text{.}\)

Une somme dénombrable de mesures sur un espace mesurable \((\Omega,\mathscr T)\) est une mesure sur \((\Omega,\mathscr T)\text{:}\)

Exercice 2.3. Multiplication par une constante positive.

(a)

Soit \((\Omega,\mathscr T, \mu)\) un espace mesuré, \(\alpha \geq 0\text{.}\) Montrer que \(\nu = \alpha \mu\) est une mesure sur \((\Omega,\mathscr T)\text{.}\)

Spoiler.

Armé de ces deux propriétés, on a donc:

Exercice 2.4. Mesure de comptage sur \((\mathbb N, \mathcal P(\mathbb N))\).

(a)

Montrer que l'application:

\begin{align*} \mu: \mathcal P(\mathbb N)\amp \rightarrow \rbb 0,+\infty\lbb \\ A \amp \mapsto \begin{cases} \text{Card}(A) \text{ si } A \text{ fini,}\\ +\infty \text{ sinon.} \end{cases} \end{align*}

définit une mesure sur \((\mathbb N, \mathcal P(\mathbb N))\text{.}\)

Remarque: En fait, on peut définir de cette façon une mesure sur \((X,\mathcal P(X))\) pour tout ensemble \(X\text{.}\)

Spoiler.

(b)

Montrer que \(\mu = \sum_{n\in \mathbb N} \delta_n\text{.}\)

Spoiler.

En fait, toutes les mesures sur \((\mathbb N, \mathcal P(\mathbb N))\) peuvent s'exprimer à l'aide de mesures de Dirac:

Exercice 2.5. Mesures sur \((\mathbb N, \mathcal P(\mathbb N))\).

(a)

Sur l'espace mesurable \((\N,\mathcal P(\N))\text{,}\) on définit

\begin{equation*} \nu : A\in \mathcal P(\N) \mapsto \begin{cases} 0 \text{ si } A=\emptyset \\ \sum_{k\in A} \frac1{2^k} \text{ sinon.} \end{cases} \end{equation*}

Calculer \(\mu(\{0\}\text{,}\) \(\mu(\{1,3\})\) et \(\mu(\N)\text{.}\)

Spoiler.

(b)

Montrer \(\mu\) définit une mesure finie sur \((\N,\mathcal P(\N))\text{.}\)

Spoiler.

(c)

Montrer que si \(\mu\) est une mesure sur \((\mathbb N, \mathcal P(\mathbb N))\text{,}\) alors il existe une suite \((u_n)_n\in (\overline R_+)^\mathbb{N}\) telle que

\begin{equation*} \mu = \sum_{n\in \mathbb N}u_n\delta_n \end{equation*}

Spoiler.

(d)

Quelle est la suite \((u_n)_n\) correspondant à la mesure de comptage ?

Exercice 2.6.

On considère la fonction partie entière \(E:\R \rightarrow \mathbb Z\) et on pose

\begin{equation*} m:A\in\mathcal P(\mathbb Z) \mapsto \mu(E^{-1}(A)) \in \rbb 0,+\infty\lbb \end{equation*}

où \(\mu\) est la mesure de Borel sur \(\R\text{.}\)

(a)

Montrer que pour tout \(k\in\mathbb Z\text{,}\) \(E^{-1}(\{k\})\in\mathscr B(\R)\text{.}\)

Spoiler.

(b)

En déduire que \(m\) est bien définie sur \(\mathcal P(\mathbb Z)\text{.}\)

Indice.

Autrement dit, montrer que , pour tout \(A\subset \mathbb Z\text{,}\) \(E^{-1}(A)\in \mathscr B(\R)\text{.}\)

Spoiler.

(c)

Montrer que \(m\) est une mesure positive sur l'espace mesurable \((\mathbb Z,\mathcal P(\mathbb Z))\text{.}\)

Spoiler.

(d)

Montrer que si \(A\subset \mathbb Z\) est un sous-ensemble fini, alors

\begin{equation*} m(A)=\Card(A) \end{equation*}

Spoiler.

Exercice 2.7.

Soit \(f:\rbb 0,3\rbb \rightarrow \R\) une fonction continue sur \(\rbb 0,3\rbb \text{.}\) On définit

\begin{equation*} m:B\in\mathscr B(\R) \mapsto \mu(f^{-1}(B)) \in \rbb 0,+\infty\lbb \end{equation*}

où \(\mu\) est la mesure de Borel sur \(\rbb 0,3\rbb \text{.}\)

(a)

Justifier que, pour tous réels \(a \lt b\text{,}\) \(f^{-1}(\lbb a,b\rbb )\in\mathscr B(\rbb 0,3\rbb )\text{.}\)

Spoiler.

(b)

On rappelle que l'ensemble

\begin{equation*} \mathscr T = \{A\subset \R, f^{-1}(A)\in\mathscr B(\rbb 0,3\rbb )\} \end{equation*}

Montrer que \(\mathscr B(\R)\subset \mathscr T\) et en déduire que \(m\) est bien définie sur \(\mathscr B(\R)\text{.}\)

Spoiler.

(c)

Montrer que \(m\) est une mesure positive sur l'espace mesurable \((\R,\mathscr B(\R))\text{.}\)

Spoiler.

(d)

Montrer que \(m(\R)=3\text{.}\) En déduire que \(m\) est une mesure finie.

Spoiler.

(e)

Supposons que \(f\) soit la fonction constante égale à 17. Montrer que, pour tout \(B\in\mathscr B(\R)\text{,}\)

\begin{equation*} m(B)=\begin{cases}3\text{ si } 17 \in B\\ 0 \text{ si } 17 \notin B\end{cases} \end{equation*}

Connaissez-vous un autre nom pour cette mesure ?

Spoiler.

Exercice 2.8.

Soit \(m:\mathcal P(\R) \rightarrow \rbb 0,+\infty \lbb\) une mesure positive sur l'espace mesurable \((\R,\mathcal P(\R))\text{.}\) On suppose que

\begin{equation*} \forall a \in\R, m(\lbb -\infty,a\lbb )=0 \end{equation*}

(a)

Montrer que \(m(\R)=0\text{.}\)

Indice.

Ecrire \(\R\) sous forme d'union dénombrable d'intervalles de la forme \(\lbb -\infty,a\lbb \text{.}\)

(b)

Montrer que

\begin{equation*} \mathscr T := \{B\in\mathcal P(\R),m(B)=0\} \end{equation*}

est une tribu de parties de \(\R\text{.}\)

(c)

Montrer que \(\mathscr B(\R) \subset \mathscr T\text{.}\)

Exercice 2.9. Mesure conditionnelle..

(a)

Soit \((\Omega,\mathscr T,\mu)\) un espace mesuré, et soit \(B\in \mathscr T\) tel que \(\mu(B)\gt 0\text{.}\) Montrer que l'application:

\begin{align*} \mu(\,\cdot\, |B):\mathscr T \amp \rightarrow \rbb 0,\infty\lbb \\ A \amp \mapsto \frac{\mu(A\cap B)}{\mu(B)} \end{align*}

définit une mesure sur \((\Omega,\mathscr T)\text{.}\)

Spoiler.

Exercice 2.10.

Dans \(\N\text{,}\) on note

\begin{align*} T_1 \amp= \{k\in \N,\, k \text{ divisible par }3 \},\\ T_2 \amp = \{k\in \N,\, k \text{ non divisible par }3 \},\\ \Omega \amp= \{1,2,3,4,5,6\} \end{align*}

(a)

On note \(\mathcal A\) la tribu associée à la partition \(T_1\text{,}\) \(T_2\text{.}\) Quels sont les éléments de \(\mathcal A\) ?

Spoiler.

(b)

On note \(\mathscr T = \{\Omega \cap A, A\in\mathcal A\}\text{.}\) Montrer que \(\mathscr T\) est une tribu sur \(\Omega\text{.}\)

Spoiler.

(c)

On note \(\mu_C\) la mesure de comptage sur \((\N,\mathcal P(\N))\text{,}\) et on définit

\begin{equation*} m: A\in \mathcal P(\N) \mapsto \frac16\mu_C(A\cap \Omega) \end{equation*}

Montrer que \(m\) est une mesure de probabilité sur \((\N,\mathcal P(\N))\text{.}\)

Spoiler.

Exercice 2.11.

Dans \(\N\text{,}\) on note

\begin{align*} Q_1 \amp = \{k\in \N,\, k \text{ divisible par }4 \},\\ Q_2 \amp = \{k\in \N,\, k \text{ non divisible par }4 \},\\ \Omega \amp= \{2,4,6,8,10\} \end{align*}

(a)

On note \(\mathcal A\) la tribu associée à la partition \(Q_1\text{,}\) \(Q_2\text{.}\) Quels sont les éléments de \(\mathcal A\) ?

Spoiler.

(b)

On note \(\mathscr T = \{\Omega \cap A, A\in\mathcal A\}\text{.}\) Montrer que \(\mathscr T\) est une tribu sur \(\Omega\text{.}\)

Spoiler.

(c)

On note \(\mu_C\) la mesure de comptage sur \((\N,\mathcal P(\N))\text{,}\) et on définit

\begin{equation*} m: A\in \mathcal P(\N) \mapsto \frac15\mu_C(A\cap \Omega) \end{equation*}

Montrer que \(m\) est une mesure de probabilité sur \((\N,\mathcal P(\N))\text{.}\)

Spoiler.