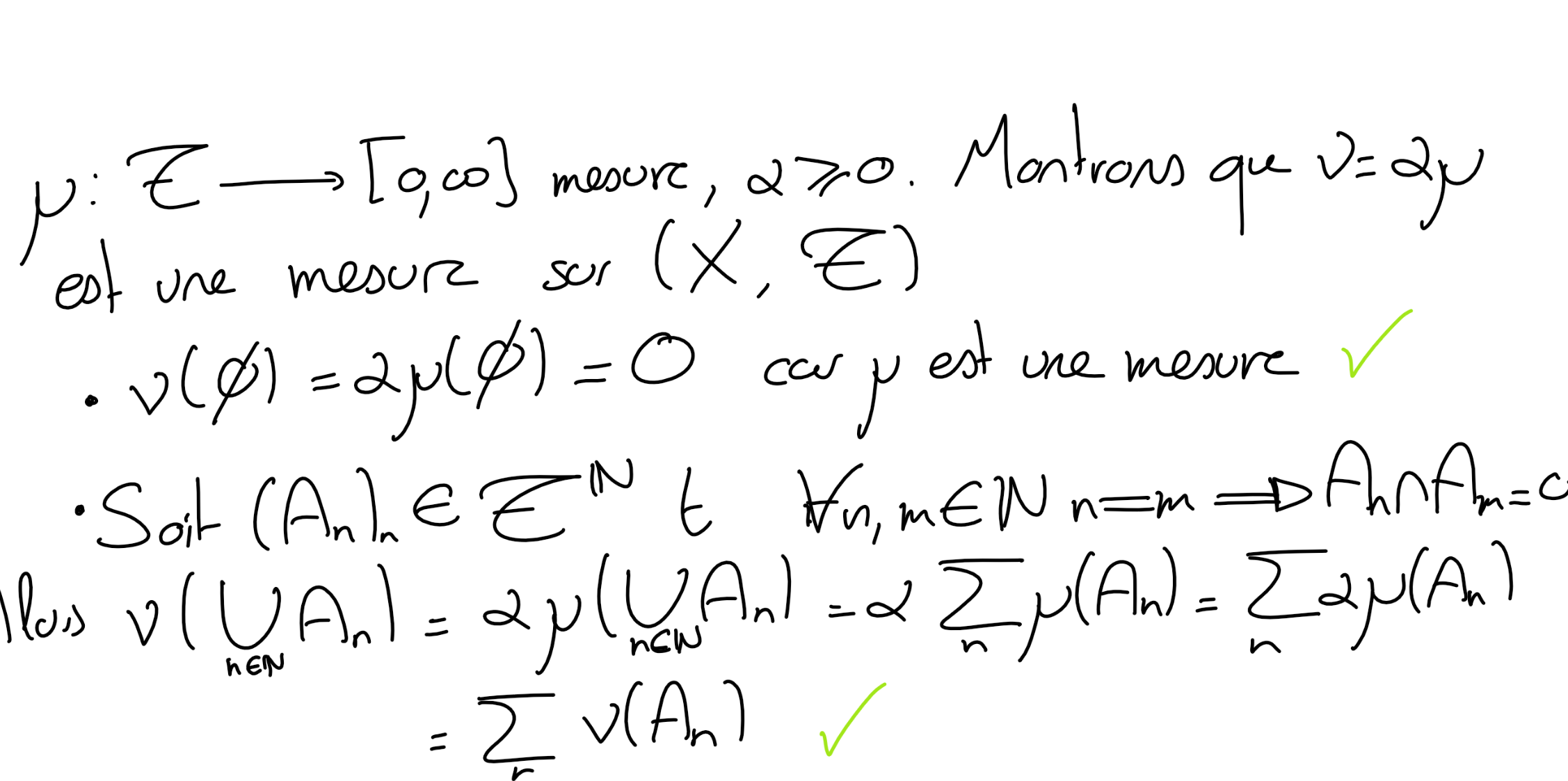Définition et premiers exemples

Section 4.1 Définition et premiers exemples

Afin que notre théorie de la mesure donne un cadre flexible à l'intégration et aux probabilités, on va, pour le moment, se passer des propriétés spécifiques à \(\mathbb R\text{:}\) l'invariance par translation et la longueur des intervalles. On verra par la suite comment construire une mesure sur \(\mathbb R\) qui ait ces spécificités.

Définition 4.1.1. Mesure sur une tribu.

Soit \((\Omega,\mathscr T)\) un espace mesurable. On appelle mesure (positive) sur \((\Omega,\mathscr T)\) toute application \(\mu: \mathscr T\rightarrow \rbb 0, \infty\lbb \) telle que

\(\displaystyle \mu(\emptyset)=0\)
(Additivité dénombrable) Pour toute famille dénombrable \((A_n)_n\) d'ensembles mesurables 2 à 2 disjoints, on a

\begin{equation*} \mu \left(\bigcup A_n\right) = \sum \mu(A_n) \end{equation*}

On dit que \((\Omega,\mathscr T, \mu)\) est un espace mesuré.

Pour attribuer une probabilité à des sous-ensembles d'un univers \(\Omega\text{,}\) on veut en plus que l'évènement certain, \(\Omega\) lui -même, ait une probabilité de 1.

Définition 4.1.2.

Soit \((\Omega,\T)\) un espace mesurable.

Si \(\mu(\Omega) \lt \infty\text{,}\) on dit que \(\mu\) est une mesure finie.
Si \(\mu(\Omega)=1\text{,}\) on dit que \(\mu\) est une mesure de probabilités.

Exercice 4.1.1. Deux exemples stupides et un contre-exemple.

(a)

Soit \(X\) un ensemble, muni de la tribu \(\mathcal P(X))\text{.}\) Montrer que l'application

\begin{equation*} \mu: A \subset X \mapsto \mu(A)=0 \end{equation*}

est une mesure sur \((X,\P(X))\text{.}\)

Est-elle finie ? Est-ce une mesure de probabilité ?

(b)

Soit \(X\) un ensemble, et soit

\begin{equation*} \mathscr T_2=\{A \in \mathcal P(X),\, A \text{ dénombrable ou } A^c \text{ dénombrable }\} \end{equation*}

la tribu dont on a déjà parlé à la fin de cet exercice. Montrer que l'application

\begin{equation*} \mu: A\in\T_2 \mapsto \begin{cases} 0 \text{ si est dénombrable}\\ 42 \text{ sinon.} \end{cases} \end{equation*}

est une mesure sur \((X,\T)\text{.}\) Est-elle finie ?

En s'inspirant de \(\mu\text{,}\) trouver une mesure de probabilité sur \((X,\T)\text{.}\)

(c)

Justifier que, malgré son nom, la mesure extérieure n'est pas une mesure sur \((\R,\P(\R)\text{.}\)

Voyons maintenant deux exemples classiques, qui reviendront souvent nous hanter.

Exercice 4.1.2. La mesure de Dirac.

Soit \(X\) un ensemble, \(a\in X\text{,}\) on définit l'application

\begin{align*} \delta_a: \mathcal P(X) \amp \rightarrow \rbb 0,+\infty\lbb \\ A \amp \mapsto \begin{cases} 0 \text{ si } a\notin A\\ 1 \text{ si } a \in A \end{cases} \end{align*}

(a)

Montrer que \(\delta_a\) est une mesure sur \((X,\mathcal P(X))\text{.}\) On l'appelle mesure de Dirac en a¹.

(b)

Montrer que \(\delta_a\) est une mesure finie.

Exercice 4.1.3. Mesure de comptage sur \((X, \mathcal P(X))\).

(a)

Montrer que l'application:

\begin{align*} \mu: \mathcal P(X)\amp \rightarrow \rbb 0,+\infty\lbb \\ A \amp \mapsto \begin{cases} \text{Card}(A) \text{ si } A \text{ fini,}\\ +\infty \text{ sinon.} \end{cases} \end{align*}

définit une mesure sur \((X, \mathcal P(X))\text{.}\)

Remarque: C'est la mesure qu'on utilise le plus souvent sur \((\N,\mathcal P(N))\text{,}\) et plus généralement sur les ensembles finis ou dénombrables ².

Spoiler.

Pour fabriquer de nouvelles mesures, on peut prendre celles qu'on a déjà, les ajouter et les multiplier par des constantes positives:

Exercice 4.1.4. Somme de mesures et multiplication par une constante positive.

(a)

Soit \((X,\mathscr T, \mu)\) un espace mesuré, et soient \(\mu_1,\mu_2:\mathscr T \rightarrow \rbb 0,+\infty\lbb \) deux mesures sur \((X,\mathscr T, \mu)\text{.}\) Montrer que \(\mu_1+\mu_2\) est une mesure sur \((X,\mathscr T, \mu)\text{.}\)

(b)

Plus généralement, soit \((\mu_n)_n\) une suite de mesures positives sur \((X,\mathscr T, \mu)\text{.}\) Montrer que \(\mu=\sum_{n\in\N} \mu_n\) est aussi une mesure que \((X,\mathscr T, \mu)\text{.}\)

Spoiler.

(c)

Soit \((X,\mathscr T, \mu)\) un espace mesuré, \(\alpha \geq 0\text{.}\) Montrer que \(\nu = \alpha \mu\) est une mesure sur \((X,\mathscr T)\text{.}\)

Spoiler.

(d)

On note \(\mu\) la msure de comptage sur \((\N,\P(\N))\text{.}\)

Montrer que \(\mu = \sum_{n\in \mathbb N} \delta_n\text{.}\)

Spoiler.

(e)

Soit \((a_n)_n \in (\R^+)^\N\) une suite de réels positifs.

Montrer que

\begin{equation*} \mu_a : A\subset \N \mapsto \sum_{n\in\N}a_n\delta_n \end{equation*}

est une mesure sur \((\N,\mathcal P(\N))\text{.}\)

Montrer que \(\mu\) est \(\sigma\)-finie, et que \(\mu\) est finie ssi \((a_n)_n\) est le terme général d'une série convergente.

Spoiler.

Une classe de mesures un peu plus générale que les mesures finies s'avèrera intéressante par la suite:

Définition 4.1.3.

Soit \(\mu\) une mesure sur un ensemble mesurable \((X,\mathscr T)\text{.}\) On dit que \(\mu\) est \(\sigma\)-finie s'il existe une suite \((E_n)_n \in \mathscr T^\mathbb N\) d'ensembles mesurables, telle que

pour tout \(n\in \mathbb N\text{,}\) \(E_n\subset E_{n+1}\)
pour tout \(n\in \mathbb N\text{,}\) \(\mu(E_n)\lt \infty\)
\(X=\bigcup_n E_n\text{.}\)

Exercice 4.1.5. Exemple, contre-exemple.

(a)

Montrer que la mesure de comptage sur \((\N,\P(\N))\) est \(\sigma\)-finie.

(b)

Soit \(\Omega\) un ensemble dénombrable et \(\mu\) une mesure sur \(\Omega\text{.}\)

Trouver une condition nécessaire et suffisante pour que \(\mu\) soit \(\sigma\)-finie.

Indice.

Pour \(\omega \in \Omega\text{,}\) considérer \(\mu(\{\omega\})\text{.}\)

(c)

Montrer que la mesure de comptage \(\mu\) sur \((\mathbb R,\P(\R))\) n'est pas \(\sigma\)-finie.

Spoiler.

Si \(\mu :A\subset \R \mapsto \Card(A)\) était \(\sigma\)-finie, il existerait une famille dénombrable \((E_n)_n\) de parties de \(\mathbb R\) telle que

\(\mathbb R= \bigcup_n E_n\text{,}\)
Pour tout \(n\in\N\text{,}\) \(\mu(E_n)\lt \infty\text{.}\)

Mais alors, chaque \(E_n\) est un ensemble fini, et alors \(\mathbb R\) serait une union dénombrable d'ensembles finis, donc serait dénombrable³ , ce qui est absurde⁴.

Quelques propriétés intuitives des mesures:

Proposition 4.1.4.

Soit \((X, \mathscr T, \mu)\) un espace mesuré.

(Monotonie): Soient \(A, B\in \mathscr T\) tels que \(A\subset B\text{.}\) Alors \(\mu(A)\leq \mu(B)\text{.}\)
(Différence): Soient \(A, B\in \mathscr T\) tels que \(A\subset B\) et \(\mu(A) \lt \infty\text{.}\) Alors, \(\mu(B\setminus A) = \mu(B)-\mu(A)\text{.}\)
(Sous-additivité): Soit \((A_n)_n \in \mathscr T^\mathbb N\text{.}\) Alors

\begin{equation*} \mu\left(\bigcup_n A_n\right) \leq \sum_n \mu(A_n) \end{equation*}
(Union croissante:) Soit \((A_n)_n \in \mathscr T^\mathbb N\) tel que pour tout \(n\text{,}\) \(A_n \subset A_{n+1}\text{.}\) Alors

\begin{equation*} \mu\left(\bigcup_n A_n\right) = \lim_{n\rightarrow \infty} \mu(A_n) \end{equation*}
(Intersection décroissante:) Soit \((A_n)_n \in \mathscr T^\mathbb N\) tel que pour tout \(n\text{,}\) \(A_{n+1} \subset A_{n}\text{,}\) et tel que \(\mu(A_0) \lt \infty\text{.}\) Alors

\begin{equation*} \mu\left(\bigcap_n A_n\right) = \lim_{n\rightarrow \infty} \mu(A_n) \end{equation*}

Exercice 4.1.6. Preuve.

(a)

Démontrer que \(\mu\) est monotone.

Spoiler.

Soient \(A, B\) tels que \(A\subset B\text{.}\) Alors \(B=A \cup (B\setminus A)\) donc, par additivité,

\begin{equation*} \mu(B) = \mu(A)+\mu(B\setminus A) \geq \mu(A) \end{equation*}

(b)

Démonter la deuxième propriété (calcul de la mesure d'une différence ensembliste)

Spoiler.

Reprenons la preuve de la monotonie : si \(\mu(A) \lt \infty\text{,}\) alors on peut soustraire \(\mu(A)\) de part et d'autre de l'égalité, ce qui donne

\begin{equation*} \mu(B\setminus A) = \mu(B)-\mu(A) \end{equation*}

(c)

Démontrer que \(\mu\) est sous-additive

Indice.

Construire, à partir des \((A_n)_n\) une suite d'ensembles mesurables disjoints, puis utiliser la \(\sigma\)-additivité de \(\mu\text{.}\)

Spoiler.

Posons \(B_0 = A_0\) et, pour tout \(n\geq 1\text{,}\)

\begin{equation*} B_n = A_n \setminus \bigcup_{k=0}^{n-1} A_k. \end{equation*}

Alors, la suite \((B_n)_n\) vérifie

\begin{equation*} \begin{cases} B_n \subset A_n \text{ donc } \mu(B_n) \leq \mu(A_n)\\ \bigcup_{k=0}^{n} A_k = \bigcup_{k=0}^{n} B_k\\ n \neq m \rightarrow B_n \cap B_m = \emptyset. \end{cases} \end{equation*}

On a donc, pour \(n\in \mathbb N\)

\begin{equation*} \mu\left(\bigcup_{k=0}^{n} A_k\right) =\mu\left(\bigcup_{k=0}^{n} B_k\right) =\sum_{k=0}^n \mu(B_k) \leq \sum_{k=0}^n \mu(A_k), \end{equation*}

d'où le résultat, par passage à la limite quand \(n\rightarrow \infty.\)

(d)

Montrer la propriété sur les unions croissantes.

Indice.

Construire à nouveau une suite disjointe.

Spoiler.

On poset \(B_0 = A_0\) et, pour tout \(n\geq 1\text{,}\)

\begin{equation*} B_n = A_n \setminus A_{n-1} \end{equation*}

Alors les \(B_n\) sont deux à deux disjoints et, pour tout \(n\text{,}\)

\begin{equation*} A_n = \bigcup_{k=0}^{n} B_k \end{equation*}

donc

\begin{align*} \mu(A_n) \amp= \mu\left(\bigcup_{k=0}^{n} B_k\right)\\ \amp = \sum_{k=0}^n \mu(B_k) \xrightarrow{n \rightarrow \infty} \mu\left(\bigcup_{k\geq 0} B_k\right)\\ \amp = \mu\left(\bigcup_{k\geq0} A_k\right). \end{align*}

(e)

....Devinez ce qu'il reste à faire, et faites-le.

Spoiler.

Posons, pour tout \(n\in \mathbb N\text{,}\) \(B_n= A_0 \setminus A_n\text{.}\)

Alors \((B_n)_n\) est une suite croissante de \(\mathscr T\) et \(\bigcup_n B_n = A_0 \setminus \bigcap_n A_n\text{.}\)

Puisque \(\mu(A_0)\lt \infty\text{,}\) on a par la propriété 2.:

\begin{align*} \mu(A_0) - \mu\left(\bigcap_{n\geq 0} A_n\right)\amp = \mu\left(\bigcup_{n\geq 0} B_n\right)\\ \amp = \lim_{n\rightarrow \infty} \mu(B_n)\\ \amp = \mu(A_0) - \lim_{n\rightarrow \infty}\mu(A_n). \end{align*}

(f)

Considérons \((\mathbb N, \mathcal P(\mathbb N))\) muni de la mesure de comptage et posons, pour \(n\in \mathbb N\text{,}\)

\begin{equation*} A_n=\{n, n+1,\dots\}=\{k\in\N,k\geq n\} \end{equation*}

Calculer \(\mu\left(\bigcap_n A_n\right)\) et \(\lim_{n\rightarrow \infty} \mu(A_n)\text{.}\) Quel est le problème ?

Spoiler.

Pour tout \(n\in\N\text{,}\) \(\mu(A_n)= \infty\) donc, dans \(\Rb\text{,}\)

\begin{equation*} \mu(A_n)\xrightarrow[n\rightarrow\infty]{}+\infty \end{equation*}

D'un autre côté,

\begin{equation*} \bigcap_{n \in \mathbb N} A_n =\{k\in\N, \forall n\in\N ,k\geq n\}= \emptyset \end{equation*}

donc \(\mu\left(\bigcap_n A_n\right) = 0\text{.}\)

On a donc

\begin{equation*} \mu(A_n)=+\infty\nrightarrow \mu\left(\bigcap_n A_n\right) = 0. \end{equation*}

Pourtant, la suite d'ensembles \((A_n)_n\) est bien décroissante: pour tout \(n\in\N\text{,}\) \(A_n \supset A_{n+1}\text{.}\)

Le problème, c'est que \(\boxed{\mu(A_0)=+\infty}\text{,}\) ce qui fait tout rater.

Parenthèse culturelle: l'idée de la mesure de Dirac a des ancêtres dans les travaux de Fourier et Cauchy, et représente, en physique, une charge électrique ou une masse concentrée en un seul point. La notation \(\delta_p\) fut introduite par le physicien Paul Dirac, un des fondateurs de la mécanique quantique, comme une généralisation ``continue'' des symboles de Kronecker \(\delta_{ij}\text{.}\)

En anglais, ces ensembles s'appellent "countable sets". Ceux qu'on peut compter, donc. D'où l'idée...de compter.

Voir ici, question (e).

Voir là.