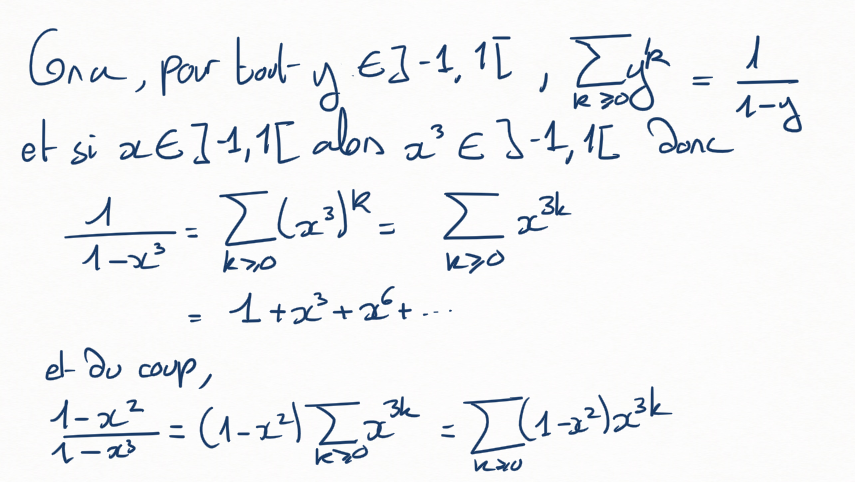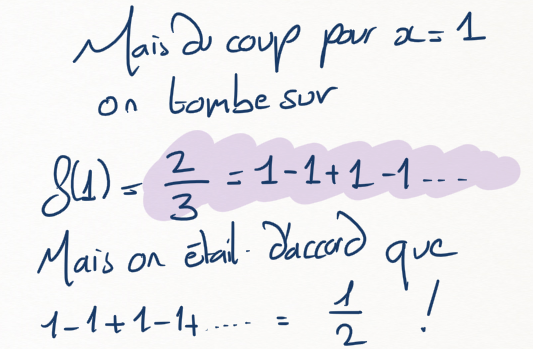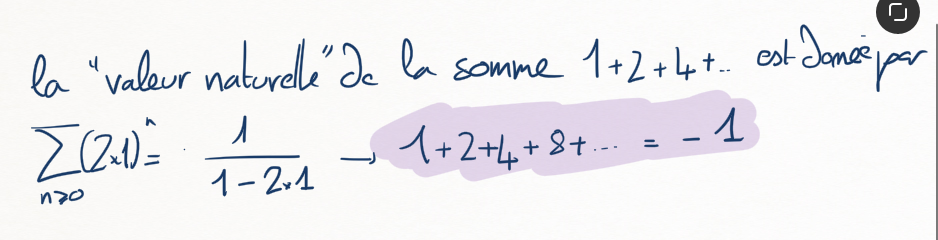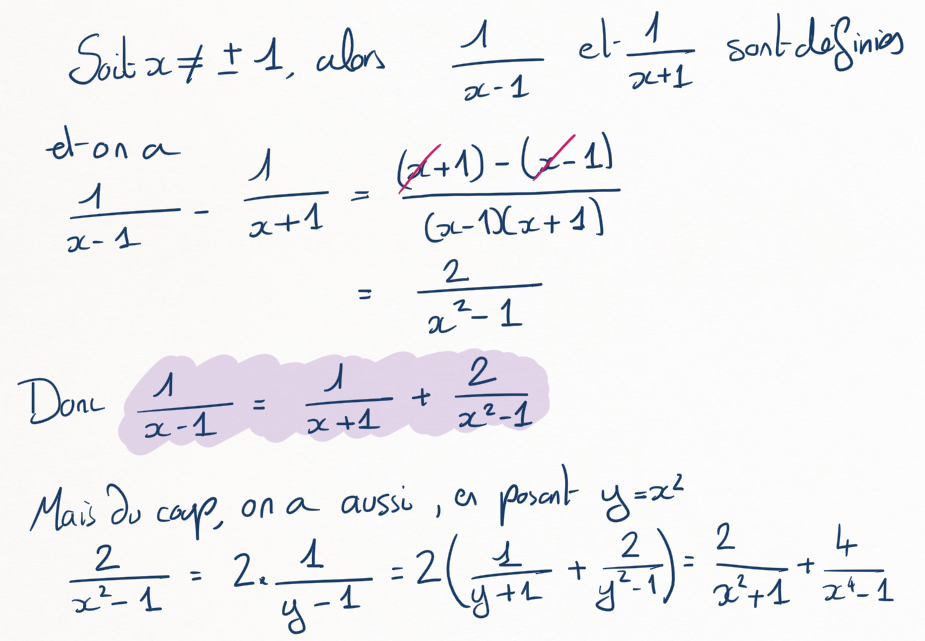Sommes des entiers - oui, tous

Section 6.1 Abel répand la lumière sur toute cette obscurité

Malgré toute la créativité déployée, il commence à devenir à peu près clair que les méthodes de sommations de séries divergentes basées sur des sommes intermédiaires et des moyennes, même pondérées avec goût, ne nous donneront aucune bonne raison de croire que la somme des entiers fait, en fait, \(-\frac1{12}\text{.}\)

Il va nous falloir une façon radicalement différente d'aborder le problème, et c'est Niels Abel qui va nous donner la prochaine étape.

Je consacrerai toutes mes forces à répandre de la lumière sur l’immense obscurité qui règne aujourd’hui dans l’Analyse. Elle est tellement dépourvue de tout plan et de tout système, qu’on s’étonne seulement qu’il y ait tant de gens qui s’y livrent—et ce qui pis est, elle manque absolument de rigueur.

―Niels Henrik Abel, dans une lettre à son professeur B. Holmboe

¹

Et Abel joignit le geste à la parole, en attaquant les séries divergentes par le biais de limites, non pas de sommes mais de fonctions.

Et en fait, historiquement, c'est cette méthode de traitement des séries divergentes qui est arrivée en premier.

Les sommes infinies étaient devenues incontournables pendant le développement de l'analyse par Newton, Leibniz et Euler à la fin du XVIIème siècle: une intégrale, finalement, c'est une somme infinie d'aires de rectangles.

Elles étaient donc utilisées avec allégresse, qu'elles tradi-convergent ou non, avec un certain, disons, dédain pour ce qu'on appellerait maintenant la rigueur mathématique.

Quoique, comme le fait remarquer Hardy, ce n'est pas la rigueur qui faisait défaut aux premiers analystes, dont la technique était irréprochable, mais plutôt les définitions. A cette époque, la tradition de préciser le sens de chaque terme qu'on emploie n'était pas établie, et ne semblait pas nécessaire: on voit bien de quoi ça parle ! Et notamment, il n'y avait aucune définition de ce qu'on appelle ici tradi-converger².

Euler, par exemple, estimait que toute série \(a_0+a_1+...\) a une somme "naturelle": quand c'est une série qu'on dirait maintenant (tradi-)convergente, il s'agit de la somme "traditionnelle"; quand c'est une série divergente, il l'obtient en utilisant "l'expression analytique associée": par exemple, à \(1-1+1-1+...\) correspond l'expression analytique

L'idée est donc une sorte d'interversion de limite:

Ou, plus généralement, si on a des fonctions (continues) \(f_n\) telles que \(f_n(x*)=a_n\) pour tout \(n\text{,}\) alors on pose

Euler obtient également de cette façon que \(1-2+3-4+...\) donne \(\frac14\) et \(1-4+9-16+...\) donne \(0\text{.}\)

A priori, cette histoire de ne pas se prendre la tête et faire ce qui vient naturellement semble marcher: pour la somme de Grandi, on récupère bien \(\frac12\text{,}\) etc.

Mais les interversions sauvages de limites, ça mord. Et Jean-Charles Callet, un homme contrariant, fit remarquer un paradoxe avec celle-ci.

Exercice 6.1.1. Somme déplaisante de Callet.

(a)

Montrer que, si \(x\in ]-1,1[\text{,}\)

\begin{equation*} f(x)=\frac{1+x}{1+x+x^2} = \frac{1-x^2}{1-x^3} \end{equation*}

Indice.

Multiplier par \(1-x\) au numérateur et au dénominateur.

Spoiler.

(b)

En déduire que

\begin{equation*} f(x)=\frac{1+x}{1+x+x^2} = 1-x^2+x^3-x^5+x^6-x^8+... \end{equation*}

Indice.

\begin{equation*} \frac{1-x^2}{1-x^3} = (1-x^2)\frac1{1-x^3} \end{equation*}

et on sait écrire \(\frac1{1-y}\) sous forme de somme. Qu'est-ce que ça donne pour \(y=x^3\) ?

Spoiler.

(c)

Qu'est-ce que ça donne pour \(x=1\) ?

....Est-ce que ce n'est pas un problème ?

Spoiler.

(d)

Choisissez votre fraction positive préférée \(\frac{m}{n}\text{,}\) avec \(n\gt m \geq 2\) et montrez que, pour tout \(x\in ]-1,1[\text{,}\)

\begin{align*} \frac{1+x+....+x^{m-1}}{1+x+....+x^{n-1}} \amp = \frac{1-x^m}{1-x^n}\\ \amp=1-x^m+x^n-x^{n+m}+x^{2n}-x^{2n+m}+... \end{align*}

Indice.

Pour la première égalité, penser à la formule qui donne la somme des termes d'une suite géométrique:

\begin{equation*} 1+x+x^2+...+x^k= \frac{1-x^{k+1}}{1-x} \end{equation*}

Pour la deuxième, remarquer que, puisqu'on sait écrire \(\frac1{1-y}\) sous forme de somme, on doit pouvoir écrire \(\frac1{1-x^m}\) sous forme de somme.

Spoiler.

(e)

Qu'est-ce que ça donne cette fois, pour \(x=1\) ?

Expliquer en quoi le problème a empiré.

Spoiler.

Et Callet demande: pourquoi prendrait-on la fonction \(\frac1{1-x}\text{,}\) et pas \(f(x)=\frac{1+x}{1+x+x^2}\) (ou n'importe laquelle des fonctions \(f_{\frac mn}=\frac{1+x+....+x^{m-1}}{1+x+....+x^{n-1}}\)) pour représenter la somme \(1-1+1-1+....\text{?}\)³.

Lagrange trouva une réponse à ce paradoxe: l'expression analytique qu'on obtient avec \(f(x)=\frac{1+x}{1+x+x^2}\) a des "trous": comme on a vu,

\(\leadsto\) Il manque \(x^1,x^4,...\text{,}\) en fait, il manque tous les \(x^{3k+1}\) !

Il faudrait donc écrire

Et donc, rétorque Lagrange à Callet, la somme infinie correspondante n'est pas \(1-1+1-1+...\) mais \(1+0-1+1+0-1+1+0-1....\text{.}\)

Mais...on n'a fait que saupoudrer de zéros. Ca devrait donner la même chose, non ?

C'est là qu'on voit les limites de la "valeur naturelle": on manque un peu d'arguments pour contrer ce désagréable contre-exemple. Lagrange, cependant, maintient que zéro, ce n'est pas rien (!), surtout quand il y en a beaucoup, et le justifie en arguant qu'avec l'exemple de \(\frac{1+x}{1+x+x^2}\text{,}\) on ne s'intéresse plus à la suite

mais à la suite

\(\leadsto\) Ce n'est pas la même suite, et il n'y a donc rien d'alarmant à ce que la série correspondante converge vers \(\frac23\text{.}\)

Et c'est ce que Lagrange avait conclu: la série \(\sum a_n\) converge "en moyenne" vers \(\frac23\text{.}\)

"En moyenne" sauvage plutôt que en moyenne propre à la Ernesto. Nettoyons tout ça.

Exercice 6.1.2.

(a)

Moderniser l'affirmation de Lagrange en montrant que la somme infinie \(1+0-1+1+0-1+1+0-1....\) correspond à une série \(\sum_p a_p\) Cesàro-convergente, telle que

\begin{equation*} \sum_{p= 0}^\infty a_p = \frac23 \quad [\mathcal C,1] \end{equation*}

Indice.

Du coup, on veut montrer la Cesàro-convergence de la somme correspondant à la suite

\begin{equation*} 1,0,-1,1,0,-1,1,0,-1,... \end{equation*}

\(\leadsto\) cette suite vaut 1 une fois sur trois, autrement dit \(1=a_0=a_3=a_6=...=a_{3k}...\text{,}\) la fois sur trois "suivante": \(0=a_1=a_4=a_7=...=a_{3k+1}...\text{,}\) et -1 la fois sur trois restante: \(-1=a_=a_5=a_8=...=a_{3k+2}.\)

Spoiler.

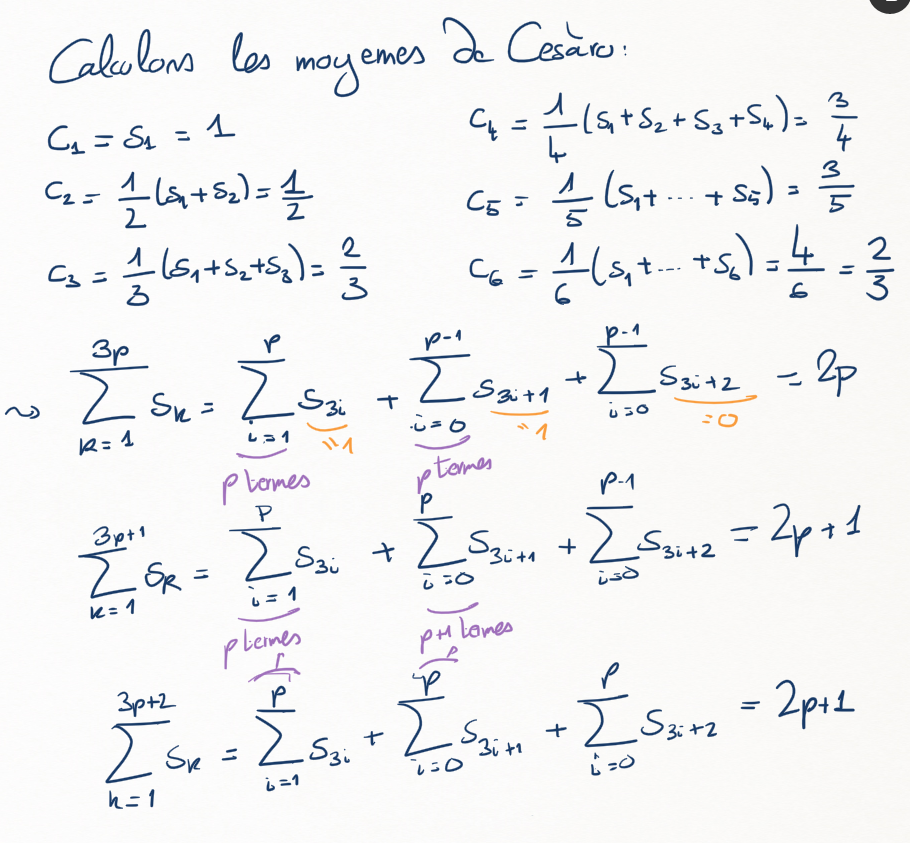
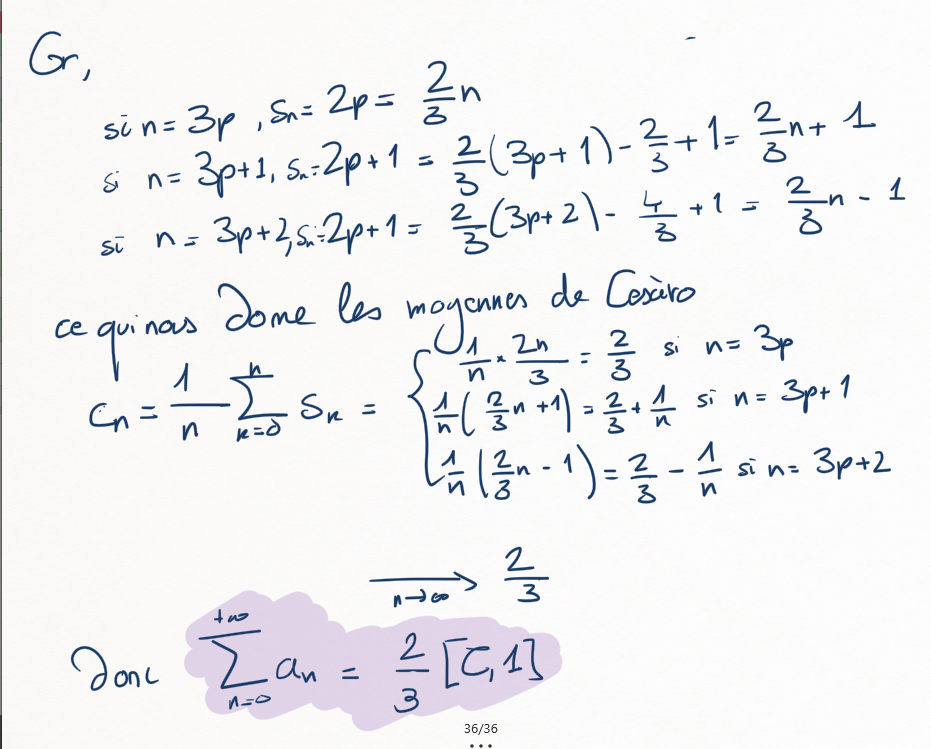
(b)

En cas d'extrême motivation: faire de même avec la somme infinie correspondant à l'"expression analytique" \(\frac{1+x+....+x^{m-1}}{1+x+....+x^{n-1}}\text{,}\) avec \(n \gt m \geq 2\text{:}\) montrer que la somme correspondante donne une série qui Cesàro-converge vers \(\frac{m}{n}\text{.}\)

Indice.

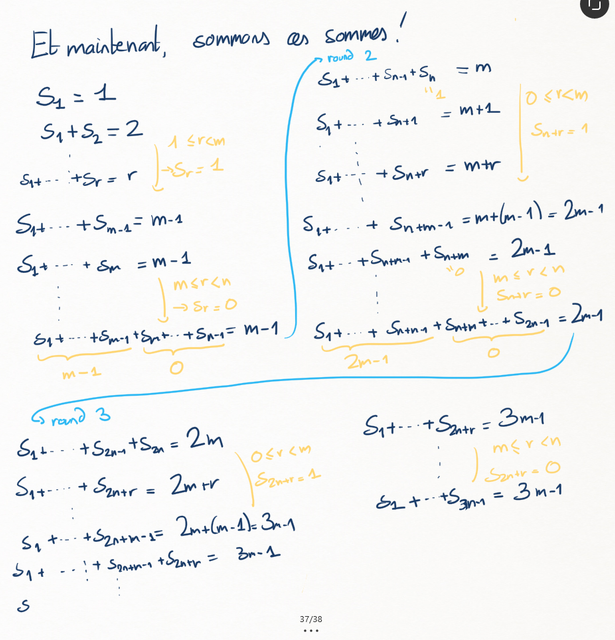
Cette fois, la suite qui nous intéresse est la suite \((a_p)_p\) telle que

\begin{equation*} \sum_{p\geq 0} a_px^p = \sum_{k\geq 0} x^{nk}-x^{nk+m} \end{equation*}

Pour la comprendre, on peut utiliser la division euclidienne de \(p\) par \(n\text{:}\) si on écrit \(p=nq+r\) avec \(0\leq r \lt n\text{,}\) on a

\begin{equation*} a_p= \begin{cases} 1\text{ si } p=nk;\\ 0\text{ si } p=nk+r,r\neq 0,m;\\ -1\text{ si } p=nk+m \end{cases} \end{equation*}

et du coup, les sommes partielles \(a_0,a_0+a_1,a_0+a_1+a_2,...\) donnent d'abord 1, jusqu'à ce qu'on atteigne \(a_m=-1\text{:}\) ça fait ensuite 0 jusqu'à ce qu'on atteigne \(a_n\text{:}\) à ce stade on ajoute 1, donc \(a_0+...+a_n=1,a_0+....+a_n+a_{n+1}=1...\) jusqu'à ce qu'on ajoute \(a_{m+n}=-1\text{,}\) après quoi ça fait à nouveau 0...

Et donc la suite des sommes partielles donne

\begin{equation*} \underbrace{1,1,....,1}_{m\text{ fois}}, \underbrace{0,0,....,0}_{n-m\text{ fois}},\underbrace{1,1,....,1}_{m\text{ fois}}, \underbrace{0,0,....,0}_{n-m\text{ fois}},... \end{equation*}

\(\leadsto\) : il y a une "proportion" de \(\frac{m}{n}\) sommes partielles qui valent 1, et une proportion de \(\frac{n-m}{n}\) qui valent \(0\text{,}\) donc "en moyenne" ça nous fait

\begin{equation*} \frac{m}{n} * 1 + \frac{n-m}{n}*0 = \frac{m}{n} \end{equation*}

C'est ce que Lagrange voulait dire par "en moyenne" ça tend vers \(\frac{m}{n}\text{.}\)

Plus qu'à l'expliciter !

Spoiler.

\(\leadsto\) Avec l'observation de Lagrange (et l'aide d'Ernesto), on se débarrasse du paradoxe: les suites \(1,-1,1,-1,...\) et \(1,0,-1,1,0,-1...\) sont différentes, donc il n'y a rien d'étonnant à ce que les fonctions qui leur sont associées par la méthode d'Abel soient différentes, et, à partir de là, que leurs sommes soient différentes.

Mais dire que zéro n'est pas rien, ce n'est pas très naturel, et si on se contente d'un passage sauvage à la limite comme on a fait plus haut, on passe facilement à côté de cette subtilité, et il est donc difficile de clarifier les choses sans établir solidement les notions de suites, de fonctions et de limites.

Une autre difficulté se présente si on remarque qu'Euler ne précise pas quel type "expression analytique" il envisage, et rien n'oblige donc à se restreindre aux "polynômes infinis" \(\sum a_n x^n \text{.}\) Ce qui peut mener à de nouveaux paradoxes :

Exercice 6.1.3.

(a)

Montrer que pour \(x\in ]-\frac12,\frac12[\text{,}\) on a

\begin{equation*} \frac1{1-2x} = 1 +2x + 4x^2+8x^3+... \end{equation*}

En déduire une possible "valeur à la Euler" de la somme \(1+2+4+....\text{.}\)

Indice.

Utiliser, d'abord raisonnablement, puis déraisonnablement, notre bonne vieille formule

\begin{equation*} 1+y+y^2+...=\frac{1}{1-y} \end{equation*}

Spoiler.

(b)

Montrer que, pour tout \(x\neq 1\text{,}\)

\begin{equation*} \frac{1}{x-1}=\frac{1}{x+1}+\frac{2}{x^2-1} \end{equation*}

et en déduire que, pour tout \(y\gt 0\text{,}\)

\begin{equation*} \frac{2}{e^{2y}-1}=\frac{2}{e^{2y}+1}+ \frac{4}{e^{4y}+1} +\frac{8}{e^{8y}+1}+... \end{equation*}

En voilà une belle expression analytique ! En déduire une autre valeur à la Euler pour \(1+2+4+....\)

Spoiler.

(c)

Montrer que pour tout \(x\in[0,1[\text{,}\)

\begin{equation*} x+(3x^2-x)+(7x^4 - 3x^2)+(15x^8-7x^4)+....=0 \end{equation*}

et en déduire une troisième possibilité pour la Euler-somme de \(1+2+4+...\text{.}\)

Spoiler.

...Ok, mais du coup, la somme \(1+2+4+8+...\text{,}\) ça fait \(-1,0\) ou \(+\infty\) ?

Ok, alors pourquoi ne pas se restreindre aux "polynômes infinis" qui semblent donner la bonne réponse plus souvent ?

L'ennui, c'est qu'Euler, et surtout ses successeurs Fourier et Poisson, comptent bien s'en servir dans d'autre cas que les "polynômes infinis": ils s'intéressent notamment à des séries trigonométriques du type

Ce qui présente à nouveau tout un tas de paradoxes, dont un qui énervait particulièrement Abel:

Les séries divergentes sont une invention du diable et c’est une honte qu’on ose fonder sur elles la moindre démonstration. On peut tirer d’elles tout ce qu’on veut quand on les emploie et ce sont elles qui ont produit tant d’échecs et tant de paradoxes.

[…] L'exemple suivant montre comme on peut se tromper. On peut démontrer rigoureusement qu'on aura pour toutes les valeurs de \(x\) inférieures à \(\pi\text{,}\)

\begin{equation*} \frac x2= \sin(x)-\frac12\sin(2x)+\frac13\sin(3x)-.etc. \end{equation*}

Il me semble qu'on pourrait conclure que la même formule aurait lieu pour \(x=\pi\text{;}\) mais cela donne

\begin{equation*} \frac{\pi}2= \sin(\pi)-\frac12\sin(2\pi)+\frac13\sin(3\pi)-.etc.=0 \end{equation*}

résultat absurde. On peut trouver une infinité d'exemples pareils.

―Niels Henrik Abel, toujours dans une lettre à Holmboe.

Exercice 6.1.4. Goutte d'eau qui fait déborder le vase.

(a)

Montrer que si \(x\in ]-\pi,\pi[\text{,}\) la série

\begin{equation*} \sum \frac{(-1)^{n+1}\sin(nx))}{n} \end{equation*}

est convergente.

⚠ Cette preuve fait appel à des outils un peu plus avancés que d'habitude: les nombres complexes et le critère de convergence d'Abel pour les séries. Si ça ne vous dit rien, pas de complexes⁶, passer à la suite sans plus se poser de question.

Indice 1.

On va utiliser le critère de (tradi)convergence d'Abel pour les séries:

Théorème 6.1.3.

Soit \((u_n)_n\in \R^\N\) une suite qui, pour tout \(n\in\N\text{,}\) s'écrit \(u_n=a_nb_n\) avec \((a_n)_n,(b_n)_n\) deux suites telles que

• \((a_n)_n\) est décroissante et tend vers \(0\text{.}\)

• La suite \((B_n)_n\) des sommes partielles des \((b_n)_n\) définie par \(B_n=\sum_{k=0}^n b_k\) est bornée: il existe \(M \gt 0\) tel que

  \begin{equation*} \forall\,n\in\N,|B_n|\leq M \end{equation*}

Alors la série \(\sum u_n\) tradiconverge.

On va aussi utiliser les faits divers suivants sur les nombres complexes:

• Si \(z_1,z_2,....z_p\) sont des nombres complexes: \(z_k=a_k+ ib_k\text{,}\) alors

  \begin{equation*} \Re(z_1+...+z_p)=a_1+...+a_p,\Im(z_1+...+z_p)=b_1+...+b_p \end{equation*}

  (La partie réelle/ d'une somme, c'est la somme des parties réelles/imaginaires)

• Dans le même ordre d'idée, si \(\lambda\) est un réel et \(z=a+ib\) un complexe, alors

  \begin{equation*} \Re(\lambda z) = \lambda \Re(z)=\lambda a, \Im(\lambda z) = \lambda \Im(z)=\lambda b \end{equation*}

• Pour tout réel \(x\text{,}\)

  \begin{equation*} e^{ix}=\cos(x)+i\sin(x) \end{equation*}

  donc \(\sin(x)=\Im(e^{ix})\text{.}\)

  \(\leadsto\) Ce qui permet de transformer des sommes de sinus en sommes d'exponentielles, qui ont l'avantage de ressembler à des séries géométriques.

  De plus, du coup,

  \begin{equation*} \sin(x)=\frac{e^{it}-e^{-it}}{2_i}, \cos(x)=\frac{e^{it}+e^{-it}}{2} \end{equation*}

• ...D'où on tire en plus la technique de l'angle moitié

  \begin{equation*} 1-e^{ix}=e^{i\frac{x}{2}}(e^{-i\frac{x}{2}}+e^{i\frac{x}{2}})=e^{i\frac{x}{2}}(2i\sin(\frac{x}{2})) \end{equation*}

• Pour trouver les parties réelles et imaginaires d'un quotient de complexes \(\dfrac{z_1}{z_2}=\dfrac{a_1+ib_1}{a_2+ib_2}\text{,}\) on multiplie enhaut et en bas par le conjugué de \(z_2\text{:}\)

  \begin{equation*} \frac{z_1}{z_2} = \frac{z_1\overline{z_2}}{z_2\overline{z_2}} = \frac{1}{|z_2|^2}(z_1\overline{z_2}) \end{equation*}

  \(\leadsto\) L'avantage, c'est que le produit, c'est facile à calculer, et \(\frac{1}{|z_2|^2}=\frac1{a_2^2+b_2^2}\text{,}\) c'est un réel.

Indice 2.

Et donc, pour utiliser le critère d'Abel, il s'agit de borner

\begin{equation*} B_N=\sum_{k=0}^N (-1)^{n+1}\sin(nx)) \end{equation*}

Pour cela, on note que

\begin{equation*} \sin(kx)= \Im(e^{ikx}) \end{equation*}

et qu'une somme finie de parties imaginaires de nombres complexes, c'est égal à la partie imaginaire de la somme.

Spoiler.

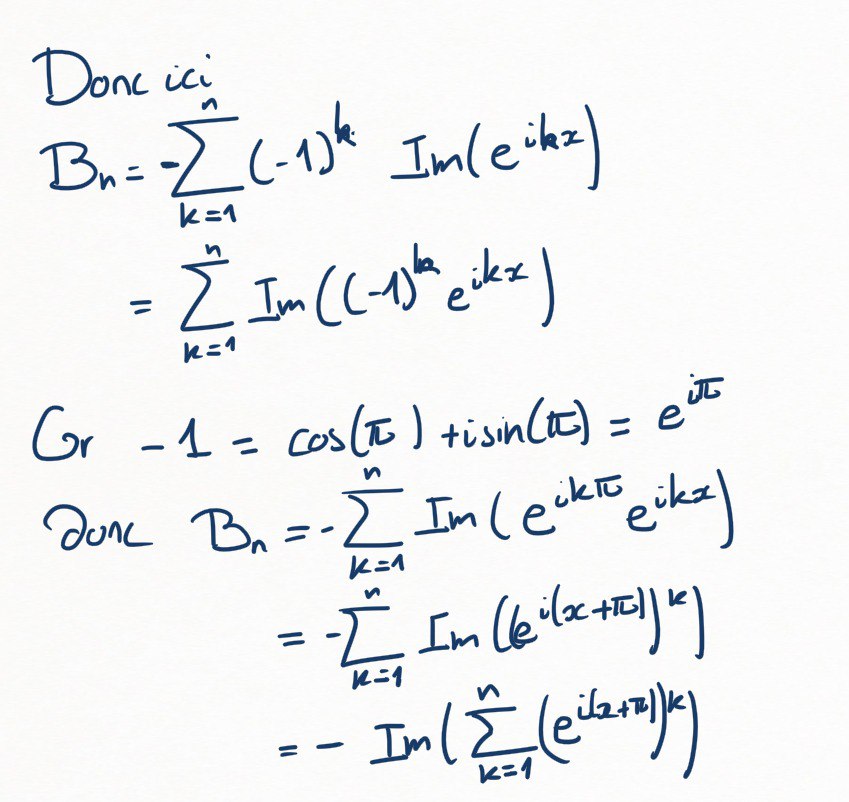
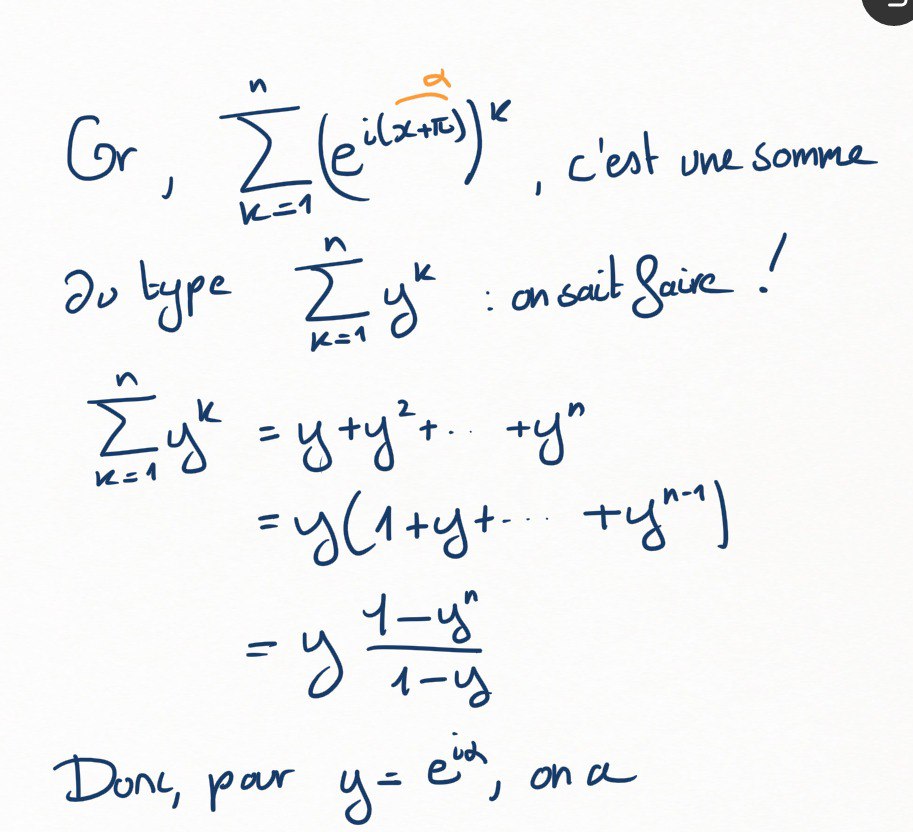
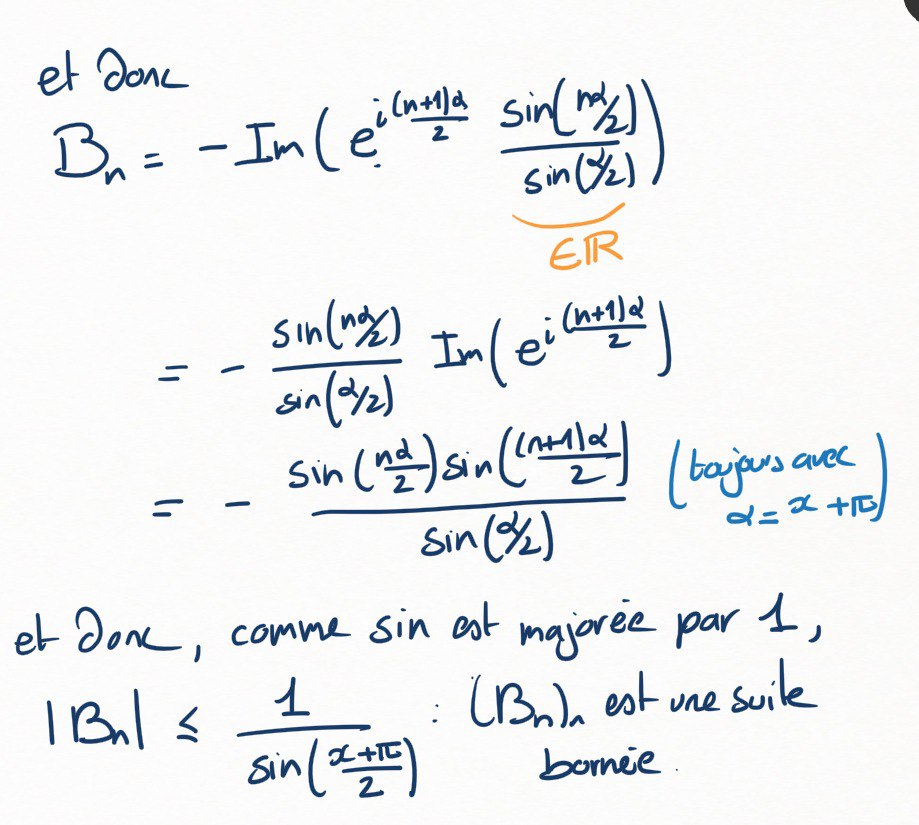
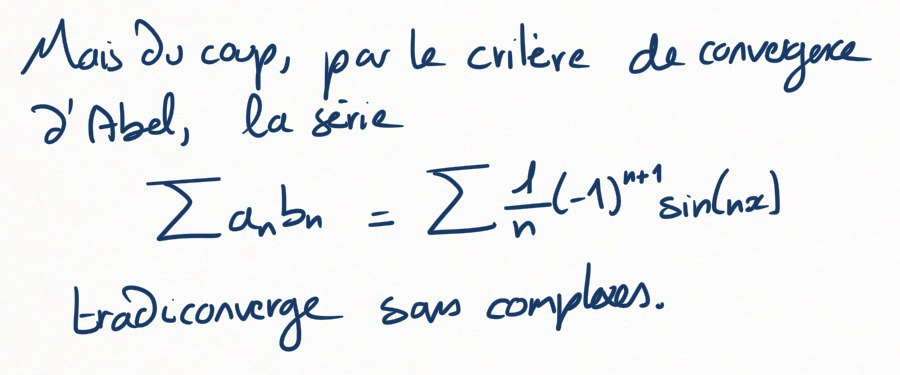
(b)

C'est la merveilleuse théorie de Fourier qui donne le résultat dont parle Abel dans la citation ci-dessus:

\begin{equation*} \sum_{n=1}^\infty \frac{(-1)^{n+1}\sin(nx))}{n} = \sin(x)-\frac12\sin(2x)+\frac13\sin(3x)-...=\frac x2 \end{equation*}

Si on suit l'art de la somme à la Euler, qu'est-ce que ça donne pour \(x=\pi\) ?

Pourquoi ça énerve Abel ?

Indice.

Combien ça fait, \(\sin(n\pi)\text{,}\) en général ?

Spoiler.

La fonction \(\frac x2\) est tout ce qu'il y a de plus définie pour \(x=\pi\text{,}\) et on a envie de dire, en faisant comme Euler, que la somme

\begin{equation*} \sum_{n=1}^\infty \frac{(-1)^{n+1}\sin(nx))}{n} \end{equation*}

a une "valeur naturelle" de \(\frac{\pi}2\text{.}\)

Mais d'un autre côté, pour tout entier \(n\text{,}\) \(\sin(n\pi)=0\) donc on se retrouve avec

\begin{equation*} \frac{pi}{2}= \sum_{n=1}^\infty \frac{(-1)^{n+1}\sin(n\pi))}{n} =\sum_{n=1}^\infty 0 \end{equation*}

et on est tenté de dire qu'une somme de zéros, même infinie, ça devrait faire 0.

(et d'ailleurs, la somme des zéros tradiconverge bien sûr vers 0!)

Et donc...\(\frac{\pi}2 =0\text{.}\) Aïe.

Ou, comme dirait Abel,

Mes amis, voici quelque chose dont il faut se moquer.

Abel entreprit alors de mettre bon ordre à tout ceci, en se basant sur le Cours d'Analyse⁷, dont il jugeait "qu'il devrait être lu par tout analyste". Dans son article de 1826, au titre engageant de "Untersuchungen über die Reihe: \(1 + \frac{m}1x + \frac{m(m - 1)}{(1\cdot 2)} x^2+ \frac{m(m - 1)(m - 2)}{(1\cdot 2\cdot 3)}x^3+ ...\)", il s'intéressa notamment à la formule du binôme

classique pour \(m\) entier, et que Newton avait généralisée à une somme infinie quand \(m\) n'est pas entier. Il s'attaqua à prouver que l'égalité est valide du moment que la somme infinie du membre de droite est convergente, un résultat utilisé mais pas (vraiment) démontré à son époque; ce faisant, il repéra quelques insuffisances dans les preuves de Cauchy, selon lequel

Lorsque les différents termes de la série sont des fonctions d'une même variable \(x\text{,}\) continues par rapport à cette variable dans le voisinage d'une valeur particulière pour laquelle la série est convergente, la somme \(s\) de la série est aussi, dans le voisinage de cette valeur particulière, fonction continue de \(x\text{.}\)

―Augustin-Louis Cauchy, Cours d'analyse de l'École royale polytechnique.

Comme Abel l'avait noté, l'horripilante série

constitue un flagrant contre-exemple à cette affirmation: tous les termes \(\frac{(-1)^{n+1}}{n}\sin(nx)\) sont continus sur \(\R\text{,}\) mais la somme présente des discontinuités à chaque point \((2m+1)\pi\text{.}\)

Il se trouve que la continuité ne suffit pas, mais il faut introduire une subtilité, une version un peu plus puissante appellée continuité uniforme. Si vous l'avez déjà croisée, vous vous êtes peut-être demandé "Pourquoi tant de haine ?"

Abel corrigea le résultat de Cauchy en introduisant des hypothèses supplémentaires similaires, pour ceux qui savent, au critère de convergence de d'Alembert, et qui impliquent la convergence uniforme.

Il ne mit pas le doigt sur exactement la bonne condition, mais ses travaux mirent sur la voie ses successeurs qui finirent enfin par mettre la main sur la continuité uniforme...plusieurs décennies plus tard.

Mais ceci est une autre histoire, qui sera contée une autre fois.

―M. Ende, L'Histoire sans fin