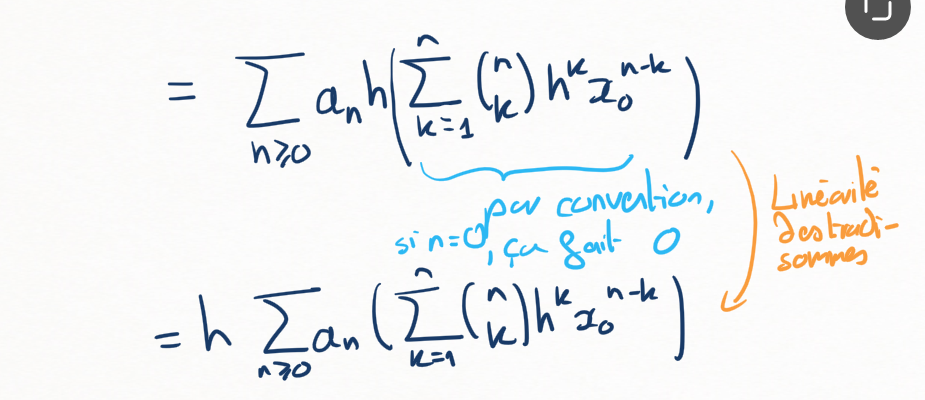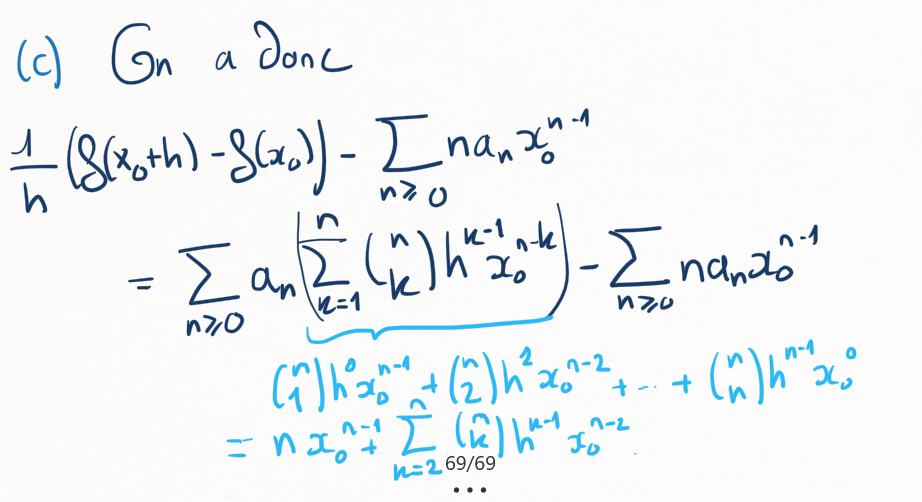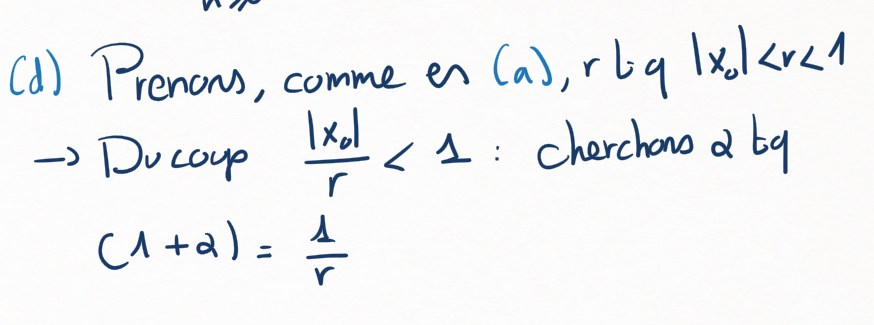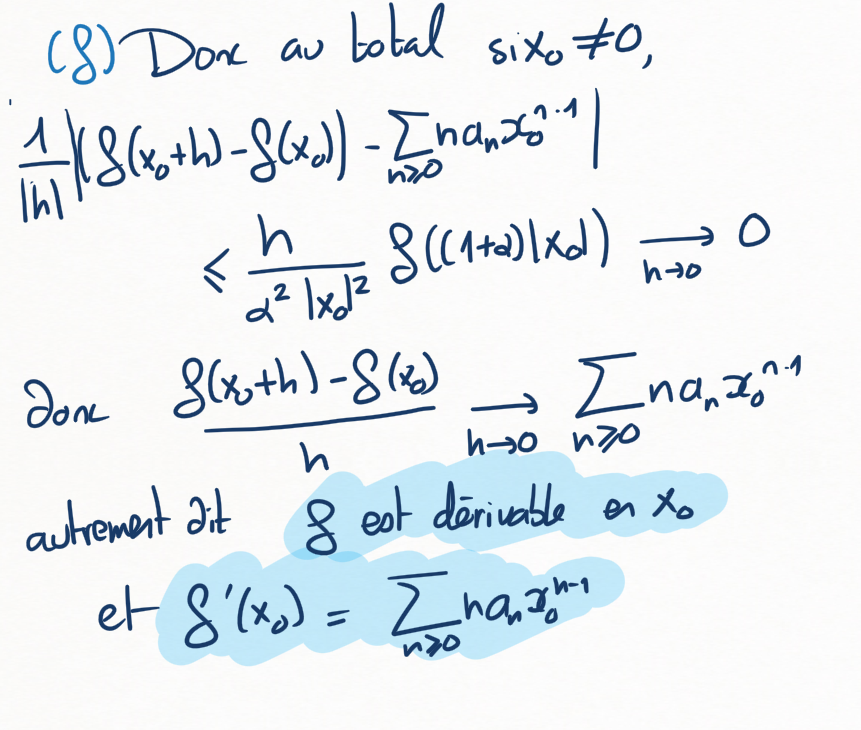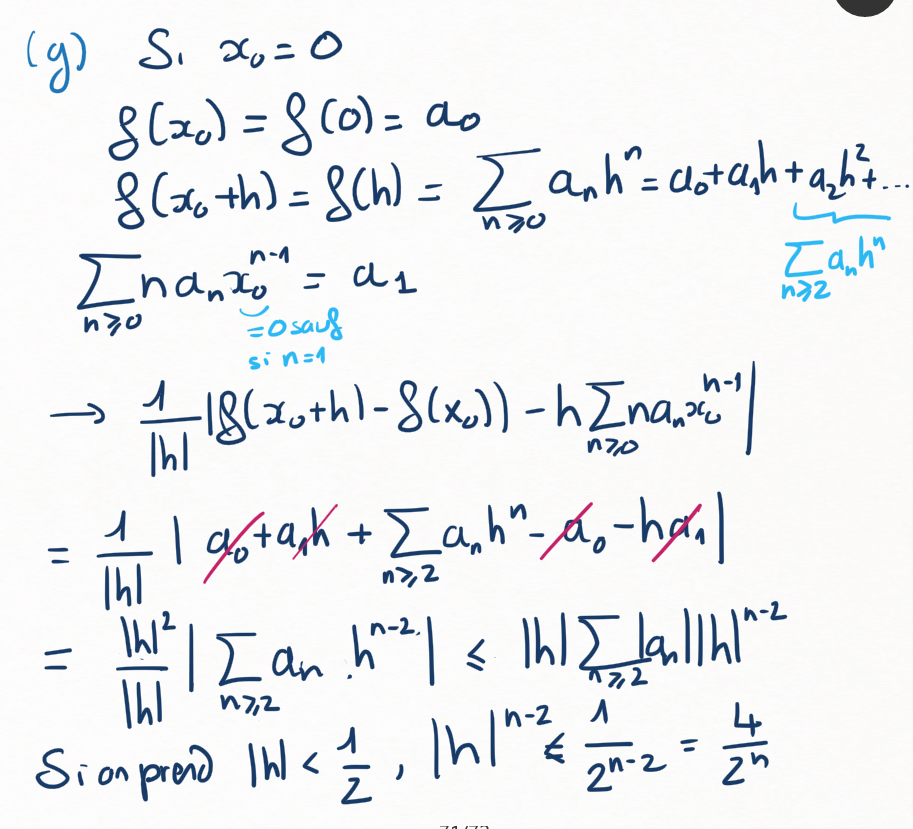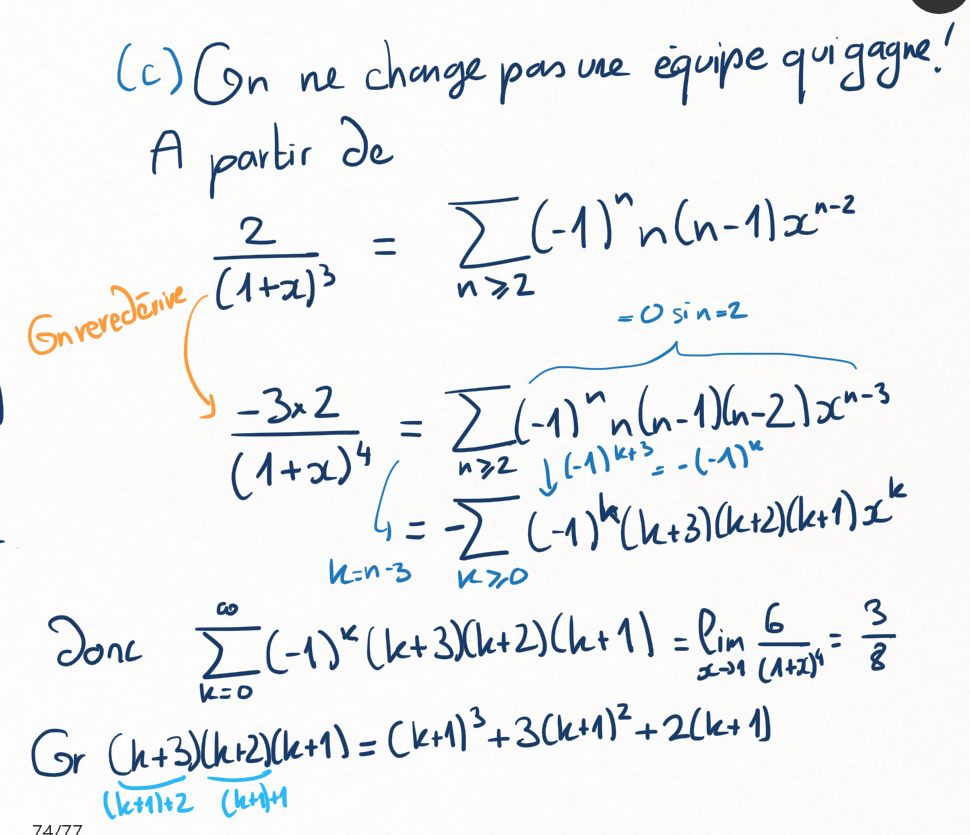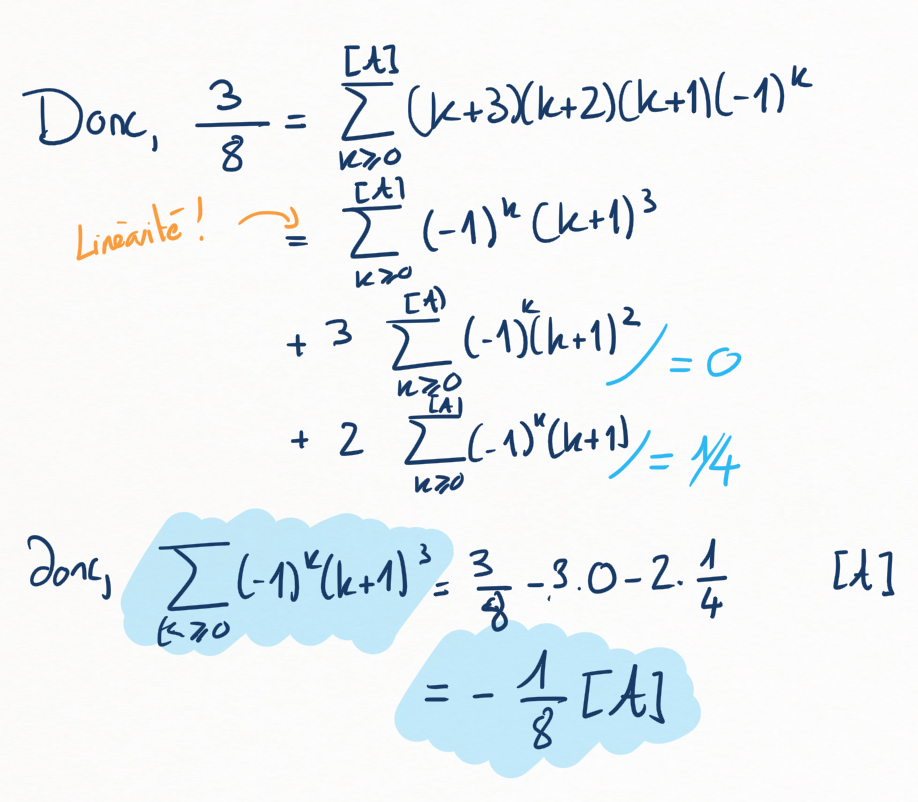Sommes des entiers - oui, tous

Section 6.4 Calculs de quelques sommes avec Abel

La sommation d'Abel repose sur la représentation des séries qu'on veut faire converger par des fonctions, dont on espère qu'elles ont une limite en \(1\text{.}\)

Un avantage des fonctions, par rapport aux suites, c'est que si elles ne sont pas trop bizarres, on dispose d'un arsenal conséquent d'outils pour les étudier. Et dans cet arsenal, une des armes les plus puissantes, c'est la \(dérivation\text{:}\)

Une brave fonction \(f:I\rightarrow \R\) est dérivable en \(x_0\) si le taux d'accroissement

converge vers quelque chose quand \(h\rightarrow 0\)¹. Dans ce cas, ce quelque chose s'appelle \(f'(x_0)\text{.}\)

Et si ça marche quel que soit \(x_0\in I\text{,}\) on récupère ainsi une nouvelle fonction \(x\in I \mapsto f'(x)\) qu'on appelle la dérivée de \(f\) et qui permet, entre autres, d'étudier les variations de \(f\text{.}\)

La bonne nouvelle, c'est que les fonctions à la Niels se laissent dériver sans heurts, et même plusieurs fois de suite, et nous permettent, à partir d'une somme qu'on connaît, d'en trouver tout un tas d'autres.

Commençons donc par vérifier que ces polynômes, bien qu'infinis, sont gentiment dérivables.

Remarquons déjà que les polynômes tout court le sont: les fonctions \(x\mapsto 1,x\mapsto x, x\mapsto x^2,...\) sont dérivables, avec

et de là, un polynôme quelconque, mettons de degré \(d\text{,}\) est dérivable:

Ou, pour l'écrire sous un format plus transportable

(On peut faire commencer la somme de droite à 0 ou à 1, selon ce qui nous arrange: de toute façon pour \(k=0\) le terme \(ka_kx^{k-1}\) donne 0)

Avec un peu de chance, on peut tout simplement remplacer \(d\) par \(+\infty\text{:}\) un calcul de séries entières

nous donnerait du coup

\(\leadsto\) Si \(f'(x)\) nous fait le plaisir d'avoir une limite quand \(x\rightarrow 1\text{,}\) on pourrait en déduire la Abel-somme de la série \(\sum na_n\) (qui semble pourtant diverger encore plus férocement que \(\sum a_n\))²

Exercice 6.4.1. Vérifions qu'on a un peu de chance.

On part donc d'une fonction "polynôme infini" du genre auquel Abel s'intéresse:

\begin{equation*} \forall x\in \lbb -1,1 \rbb,\ f(x)=\sum_{n=0}^\infty a_n x^n \end{equation*}

On va montrer que la fonction \(f\) est dérivable sur \(\lbb -1,1\rbb\text{,}\) et que

\begin{equation*} \forall x\in \lbb -1,1 \rbb,\ f'(x)=\sum_{n=0}^\infty na_n x^{n-1} \end{equation*}

(a)

Commençons par vérifier que la somme de droite

\begin{equation*} \sum_{n=0}^\infty na_n x^{n-1} \end{equation*}

existe pour tout \(x\in \lbb -1,1 \rbb\text{.}\)

Indice.

Commencer par choisir un \(x_0 \in \lbb -1, 1 \rbb\) et un \(r\) tel que \(|x_0|\lt r \lt 1 \)³. En utilisant la tradiconvergence de \(\sum a_n x^n\text{,}\) montrer que pour une constante \(M_1 \gt 0\) choisie avec goût,

\begin{equation*} 0\leq na_n x^{n-1} \leq n M_1 \left(\frac{|x_0|}{r}\right)^n \end{equation*}

Plus qu'à montrer que la série \(\sum n \left(\frac{|x_0|}{r}\right)^n \) tradiconverge !

Pour ça, montrer qu'on peut majorer \(n \left(\frac{|x_0|}{r}\right)^n \) par \(\frac{M_2}{n^2}\text{,}\) pour une certaine constante \(M_2\text{.}\)

Spoiler.

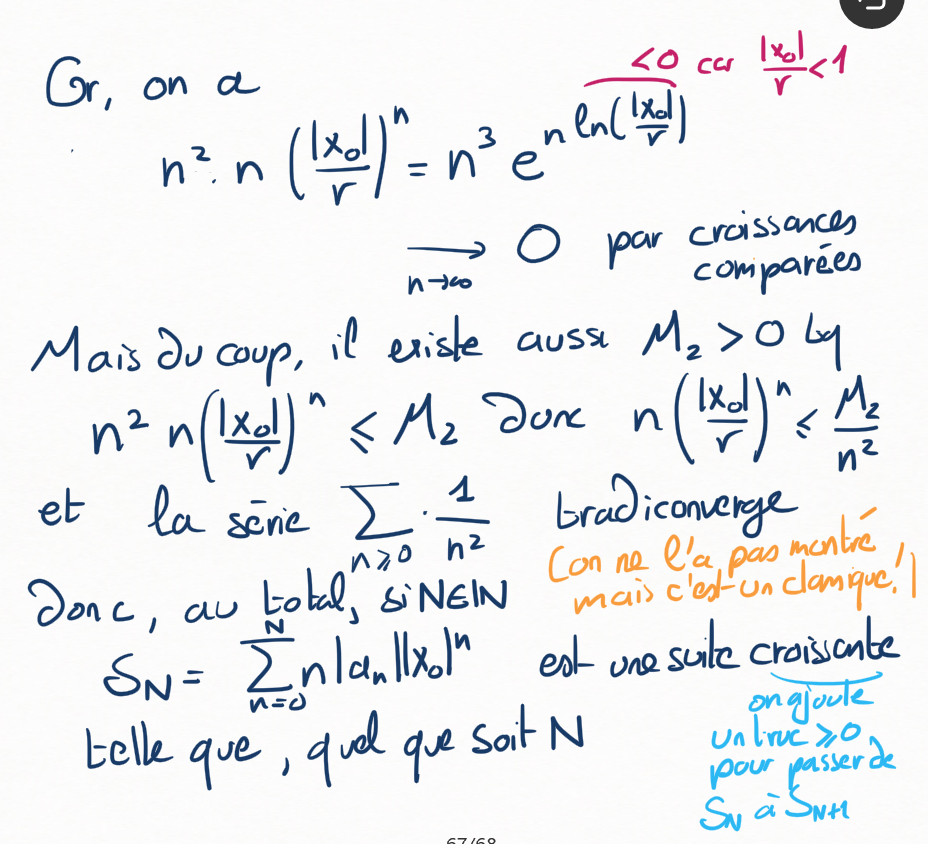
(b)

Maintenant qu'on est sûrs de ne pas aller dans le mur, il s'agit de montrer que le taux d'accroissement

\begin{equation*} \frac1h(f(x_0+h)-f(x_0)) \end{equation*}

tend vers \(\sum_{n=0}^\infty na_n x^{n-1}\) quand \(h\rightarrow 0\text{.}\)

Commençons pas nous faire une idée de la tête de ce taux d'accroissement: montrer que

\begin{equation*} f(x_0+h)-f(x_0) = h\sum_{n=0}^\infty a_n \left(\sum_{k=1}^n \binom{n}{k}h^{k-1}x_0^{n-k}\right) \end{equation*}

Indice.

On peut utiliser la formule du binôme, qui, dans le cas où elle est finie, n'énervait pas trop Abel:

\begin{equation*} (a+h)^n = \sum_{k=0}^n \binom{n}{k}h^ka^{n-k} \end{equation*}

Spoiler.

(c)

En déduire que

\begin{equation*} \frac{1}{h}(f(x_0+h)-f(x_0)) - \sum_{n=0}^\infty na_n x^{n-1} = \sum_{n=0}^\infty a_n \left(\sum_{k=2}^n \binom{n}{k}h^{k-1}x_0^{n-k}\right)= h\sum_{n=0}^\infty a_n \left(\sum_{k=2}^n \binom{n}{k}h^{k-2}x_0^{n-k}\right) \end{equation*}

Indice.

Dans la somme \(\sum_{k=1}^n \binom{n}{k}h^{k-1}x_0^{n-k}\) sur laquelle on vient de tomber, que donne le premier terme \(k=1\) ?

Spoiler.

(d)

On se retrouve donc à étudier

\begin{equation*} u_n(h) = \sum_{k=2}^n \binom{n}{k}h^{k-2}x_0^{n-k} \end{equation*}

Montrer qu'on peut trouver \(\alpha \gt 0\) tel que \((1+\alpha)|x_0| \lt 1\text{.}\)

Indice.

Comme \(|x_0| \lt 1\text{,}\) on sait qu'il y a un \(r\) tel que \(|x_0|\lt r \lt 1\text{.}\)

Peut-on construire un \(\alpha\) qui marche à partir de ce \(r\) ?

Spoiler.

(e)

En déduire que, pour tout \(n\text{,}\) si on prend \(x_0\neq 0\) et \(h\) suffisamment petit pour que \(|h| \lt \alpha |x_0|\text{,}\) alors

\begin{equation*} |u_n(h)|\leq (1+|\alpha|)^n |x_0|^n \cdot \frac{1}{\alpha^2|x_0|^2} \end{equation*}

En déduire que

\begin{equation*} \sum a_n |u_n(h)| \end{equation*}

est convergente (vers quoi, d'ailleurs ?)

Question bonus: Est-ce un problème que ça ne marche que si \(h\) est assez petit ?

Indice.

La formule du binôme, on peut l'utiliser dans les deux sens !

Spoiler.

(f)

Conclure pour le cas où \(x_0\neq 0\text{,}\) ce qui est le gros du travail !

Spoiler.

(g)

Et si \(x_0=0\) ?

Montrer que, si on prend \(h\in\lbb -\frac12, \frac12 \rbb\text{,}\)

\begin{equation*} \frac{1}{|h|}|f(h)-f(0) - ha_1|\leq 4h \sum_{n\geq 0} |a_n|\frac1{2^n} \end{equation*}

Et conclure conclusivement.

Spoiler.

Du coup, si on connaît la fonction \(f(x)\) et qu'on sait la dériver, on va pouvoir en déduire d'autres sommes.

Notamment, on avait vu⁴ que les sommes alternées

sont \((\mathcal C,p)\)-convergentes, mais on n'avait pas pu trouver leur \((\mathcal C,p)\)-somme.

Du coup, toutes ces sommes sont aussi \((\mathcal A)\)-convergentes; est-ce que Niels peut nous les calculer ?

Exercice 6.4.2. Calcul de quelques \(1^p-2^p+3^p-4^p+...\).

Partons de notre série divergente préférée: la somme de Grandi \(\sum (-1)^n\text{.}\)

Avec Abel, on avait introduit la fonction

\begin{equation*} \forall x \in \lbb -1,1\rbb, f(x)=\sum_{n=0}^\infty (-1)^n x^n = \frac1{1+x} \end{equation*}

(a)

Montrer que, pour tout \(x \in \lbb -1,1\rbb\text{,}\)

\begin{equation*} \frac1{(1+x)^2} = \sum_{n=0}^\infty (-1)^{n+1} n x^{n-1} \end{equation*}

En déduire que \(\sum (-1)^n (n+1)\) est Abel-convergente, et que

\begin{equation*} \sum_{n=0}^\infty (-1)^n (n+1) = \frac14 \quad [\mathcal A] \end{equation*}

Indice.

Qu'est-ce que ça donne si on dérive chaque terme de

\begin{equation*} \frac1{1+x} = \sum_{n=0}^\infty (-1)^n x^n \end{equation*}

avec la formule obtenue au Exercice 6.4.1 ?

Spoiler.

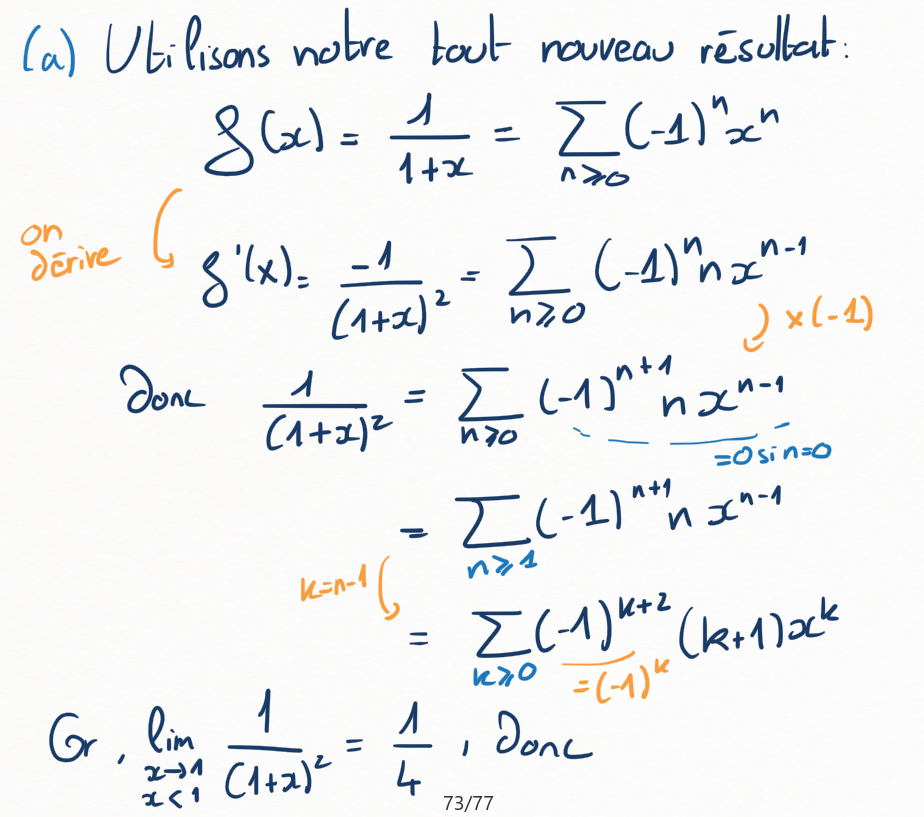
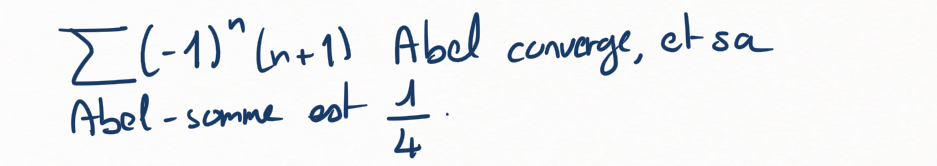
(b)

Montrer que, pour tout \(x \in \lbb -1,1\rbb\text{,}\)

\begin{equation*} \frac2{(1+x)^3} = \sum_{n=0}^\infty (-1)^{n} n(n-1) x^{n-2} \end{equation*}

En déduire que \(\sum (-1)^n (n+1)^2\) est Abel-convergente, et que

\begin{equation*} \sum_{n=0}^\infty (-1)^n (n+1)^2 = 0 \quad [\mathcal A] \end{equation*}

Indice.

A nouveau, utiliser la formule du Exercice 6.4.1 pour re-dériver

\begin{equation*} \frac1{(1+x)^2} = \sum_{n=0}^\infty (-1)^{n+1} n x^{n-1} \end{equation*}

Ca ne donne pas exactement ce qu'on veut, mais d'un autre côté on a déjà calculé

\begin{equation*} \sum_{n=0}^\infty (-1)^n (n+1) = \frac14 \end{equation*}

et on peut s'en servir !

Spoiler.

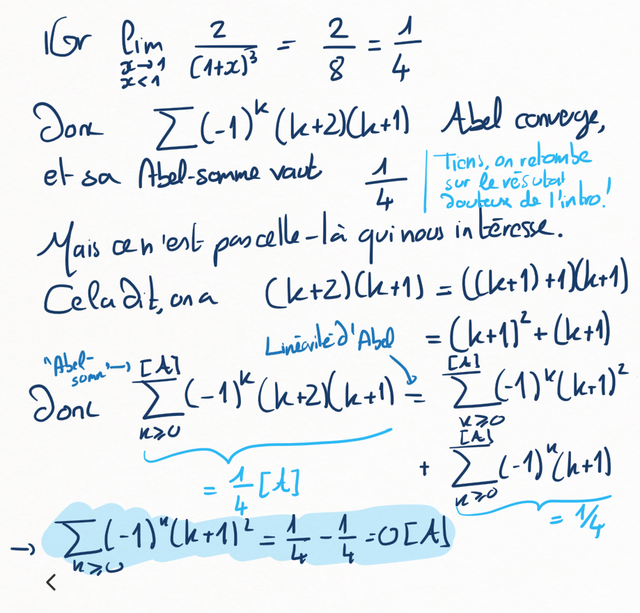
(c)

Une autre pour la route : calculer la \((\mathcal A)\)-somme de la série

\begin{equation*} \sum (-1)^n (n+1)^3 \end{equation*}

et se convaincre qu'un (long) dimanche après-midi pluvieux, on pourrait trouver un paquet de \(\sum (-1)^n (n+1)^p\) comme ça.

Spoiler.

(d)

A l'époque des Cesàro-sommes, on avait aussi obtenu les sommes alternées des coefficients binomiaux (dans la douleur):

\begin{equation*} \sum_{n=0}^\infty (-1)^n\binom{n+p}{n} = \frac 1{2^{p+1}} \quad [\mathcal C,p] \end{equation*}

A l'aide des questions précédentes, retrouver

\begin{align*} \sum_{n=0}^\infty (-1)^n\binom{n+1}{n} \amp =\frac14 \quad [\mathcal A]\\ \sum_{n=0}^\infty (-1)^n\binom{n+2}{n} \amp=\frac18 \quad [\mathcal A]\\ \sum_{n=0}^\infty (-1)^n\binom{n+3}{n} \amp=\frac1{16} \quad [\mathcal A] \end{align*}

et constater avec soulagement qu'on ne semble pas avoir trop déliré en comparant Abel avec Cesàro.

Spoiler.

(e)

En dérivant avec enthousiasme, montrer plus généralement que

\begin{equation*} \sum_{n=0}^\infty (-1)^n\binom{n+p}{n} = \frac 1{2^{p+1}} \quad [\mathcal A] \end{equation*}

Indice.

Quelle est la dérivée de

\begin{equation*} \frac1{(1+x)^p} ? \end{equation*}

et du coup quelle est la fonction qu'on trouve en dérivant \(p\) fois

\begin{equation*} f(x)=\frac1{1+x} \end{equation*}

Et d'un autre côté, qu'est ce que ça donne si on dérive \(p\) fois de suite

\begin{equation*} \sum_{n=0}^\infty (-1)^n x^n \end{equation*}

en particulier ?

Spoiler.

La dérivation allègre et répétée nous permet ainsi, par récurrence, de calculer les sommes alternées

Mais on peut en fait trouver une formule explicite⁵, qui donne leur valeur sans avoir à calculer toutes les précédentes. Cette formule fait intervenir les mystérieux nombres de Bernoulli. Faisons donc un détour pour voir de quoi il s'agit, en compagnie d'un alchimiste et de l'héritier d'une familel de samourais.