Applications linéaires continues et norme des applications linéaires

Section 8 Applications linéaires continues et norme des applications linéaires

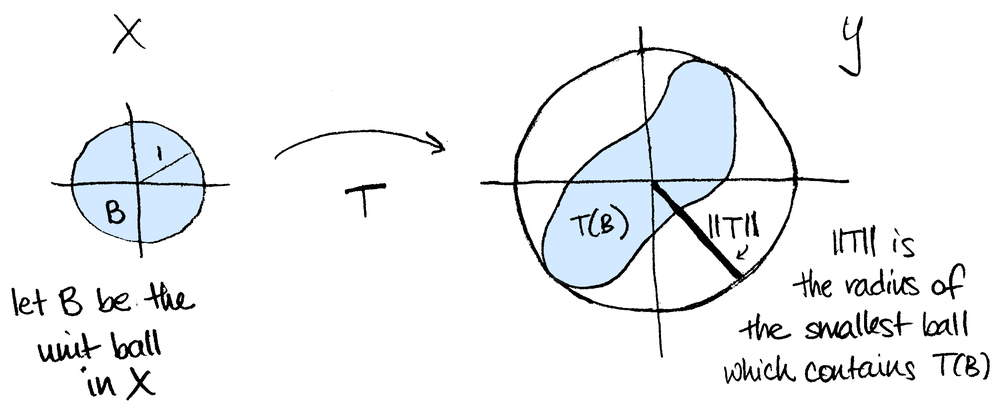
Théorème 8.2. Continuité des applications linéaires.

Soit \(f: E \rightarrow F\) une application linéaire. Alors \(f\) est continue ssi il existe \(c>0\) tel que

\begin{equation*} \forall\, x \in E,\ \|f(x)\|_F \leq c\|x\|_E. \end{equation*}

On note \(\mathcal L(E,F)\) l'ensemble des applications linéaires continues \(E \rightarrow F\text{.}\)

Théorème 8.3.

Pour tout \(f\in \mathcal L(E,F)\text{,}\) on définit

\begin{equation*} \|f\|_{\mathcal L(E,F)} = \sup_{\|x\|_E=1} \|f(x)\|_F = \sup_{x \neq 0} \frac{\|f(x)\|_F}{\|x\|_E}. \end{equation*}

Alors \(\|.\|_{\mathcal L(E,F)}\) est une norme sur l'e.v. \(\mathcal L(E,F)\text{.}\)

Méthode

Pour montrer qu'une application linéaire \(f\) est continue et calculer sa norme, on procède en deux étapes:
1. On montre qu'il existe \(c>0\) telle que
  
  \begin{equation*} \forall\, x \in E,\ \|f(x)\|_F \leq c\|x\|_E. \end{equation*}
  
  \(\leadsto\) On en déduit que \(f\) est continue et que \(\|f\|_{\mathcal L(E,F)} \leq c\text{.}\)
2. On montre que \(\|f\|_F \geq c\text{.}\)
  
  Pour cela, on cherche \(x\in E\) tel que \(\|x\|_E=1\) et \(\|f(x)\|_F=c.\text{.}\)
  
  Si on ne trouve pas de tel \(x\text{,}\) on peut aussi chercher une suite \(x_n\) telle que \(\|x_n\|=1\) et \(\|f(x_n)\| \geq c-\frac1n\text{.}\)
  
  On a alors \(\|f\|_F \geq c-\frac 1n\) pour tout \(n\text{,}\) donc \(\|f\|_F \geq c\text{.}\)
Si \(E\) est de dimension finie, toute application linéaire \(E\rightarrow F\) est continue ²
Pour montrer qu'une application linéaire n'est pas continue, on peut chercher une suite \((u_n)_n\) de \(E^\N\) telle que

\begin{equation*} \text{Pour tout } n\in\N,\ \|u_n\|=1 \end{equation*}

et

\begin{equation*} \|f(u_n)\| \rightarrow \infty. \end{equation*}

Proposition 8.4. Propriétés de la norme d'application linéaire.

\(\displaystyle \|Id_E\|_{\mathcal L(E)} = 1\)
\(\|f\circ g\| \leq \|f\|\,\|g\|\text{.}\)

En particulier, en notant

\begin{equation*} f^n=\underbrace{f \circ f \circ .... \circ f}_{n \text{fois}} \end{equation*}

on a

\begin{equation*} \|f^n\| \leq \|f\|^n. \end{equation*}
Si \(F\) est complet, alors \(\mathcal L(E,F)\) est complet.

Exercice 8.1.

On considère l'espace vectoriel \(E=\R_n[X]\) muni de la norme définie, pour \(P=\sum_{k=0}^{n}a_kX^k\) par

\begin{equation*} \|P\|=\sum_{k=0}^{n}|a_k|. \end{equation*}

On s'intéresse aux applications suivantes sur \(E\text{:}\)

\begin{align*} L_1:P\in E\amp\mapsto XP'\\ L_2: P\in E \amp\mapsto 17P \end{align*}

(a)

Montrer que \(L_1\) et \(L_2\) sont des endomorphismes de \(E\text{.}\)

(b)

Justifier (sans calcul !) que \(L_1\) et \(L_2\) sont continues.

Spoiler.

\(L_1\) et \(L_2\) sont des applications linéaires définies sur un espace vectoriel \(E=\R_n[X]\) qui est de dimension finie, donc elles sont nécessairement continues.

(c)

Montrer que \(\|L_1\|_{\mathcal L(E)}=n\) et \(\|L_2\|_{\mathcal L(E)}=17\text{.}\)

Spoiler.

Montrons que \(\|L_1\|_{\mathcal L(E)}=n\) par double inégalité:

\(\boxed{\leq}\) Soit \(P=\sum_{k=0}^n a_kX^k\in E\text{,}\) on calcule

\begin{align*} \|L_1(P)\|\amp =\left\|X\sum_{k=0}^nka_kX^{k-1}\right\| = \left\|\sum_{k=0}^nka_kX^{k}\right\|\\ \amp =\sum_{k=0}^{n}|ka_k| \\ \amp \leq n\sum_{k=0}^{n}|a_k|=n\|P\| \end{align*}

donc \(\|L_1\|_{\mathcal L(E)}\leq n\text{.}\)
\(\boxed{\geq}\) Pour \(P=X^n\) on a, d'une part, \(\|P\|=1\) et d'autre part, \(L_1(P)=nX^n\) donc \(\|L_1(P)\|=n\text{.}\) Donc

\begin{equation*} \|L_1\|_{\mathcal L(E)}=\sup_{\|P\|=1} \|L_1(P)\| \geq \|L_1(X^n)\|= n \end{equation*}

On a donc bien \(\|L_1\|_{\mathcal L(E)}=n\text{.}\)

Pour \(L_2\text{,}\) on remarque que \(L_2=17\, Id_E\) donc

\begin{equation*} \|L_2\|_{\mathcal L(E)}=\|17\,Id_E\|_{\mathcal L(E)}=17\|Id_E\|_{\mathcal L(E)}=17 \end{equation*}

(d)

En déduire que \(L:P\mapsto XP'+ 17P\) est un endormorphisme continu et majorer sa norme.

Spoiler.

\(L\) est continue car c'est une somme d'applications linéaires continues.

De plus, par inégalité triangulaire,

\begin{equation*} \|L\|_{\mathcal L(E)}=\|L_1+L_2\|_{\mathcal L(E)}\leq \|L_1\|_{\mathcal L(E)}+\|L_2\|_{\mathcal L(E)} = 17+n. \end{equation*}

Exercice 8.2.

On considère l'espace vectoriel \(E=\R[X]\) muni de la norme définie, pour \(P=\sum_{k=0}^{\deg P}a_kX^k\) par

\begin{equation*} \|P\|=\sum_{k=0}^{\deg P}|a_k|. \end{equation*}

On s'intéresse aux applications suivantes sur \(E\text{:}\)

\begin{align*} L_1:P\in E\amp\mapsto X^2 P \\ L_2: P \in E \amp\mapsto 3P\in E \end{align*}

(a)

Montrer que \(L_1\) et \(L_2\) sont des endomorphismes de \(E\text{.}\)

(b)

Montrer que \(L_1\) est continue de norme 1.

Spoiler.

Montrons que \(\|L_1\|_{\mathcal L(E)}=1\) par double inégalité:

\(\boxed{\leq}\) Soit \(P=\sum_{k=0}^n a_kX^k\in E\text{,}\) on calcule

\begin{align*} \|L_1(P)\|\amp=\left\|X^2\sum_{k=0}^na_kX^{k}\right\|\\ \amp = \left\|\sum_{k=0}^na_kX^{k+2}\right\|\\ \amp=\sum_{k=0}^{n}|a_k| =1\cdot\|P\| \end{align*}

donc \(\|L_1\|_{\mathcal L(E)}\leq 1\text{.}\)
\(\boxed{\geq}\) Pour \(P=1\) on a, d'une part, \(\|P\|=1\) et d'autre part, \(L_1(P)=X^2\) donc \(\|L_1(P)\|=1\text{.}\) Donc

\begin{equation*} \|L_1\|_{\mathcal L(E)}=\sup_{\|P\|=1} \|L_1(P)\| \geq \|L_1(1)\|= 1 \end{equation*}

On a donc bien \(\|L_1\|_{\mathcal L(E)}=1\text{.}\)

(c)

Justifier (sans calculs!) que \(L_2\) est continue de norme 3.

Spoiler.

Pour \(L_2\text{,}\) on remarque que \(L_2=3\, Id_E\) donc \(L_2\) est continue, car \(\mathcal{L}(E)\) est un espace vectoriel, et

\begin{equation*} \|L_2\|_{\mathcal L(E)}=\|3\,Id_E\|_{\mathcal L(E)}=3\|Id_E\|_{\mathcal L(E)}=3 \end{equation*}

(d)

En déduire que \(L:P\mapsto (X^2+3)P\) est un endormorphisme continu de \(E\) et majorer sa norme.

Exercice 8.3.

On considère l'espace vectoriel \(E\) des suites réelles convergentes:

\begin{equation*} E=\{(u_n)_n \in \R^\N, \exists \ell\in \R, u_n \xrightarrow[]{n\rightarrow \infty}\ell\} \end{equation*}

muni de la norme \(\|(u_n)_n\|_\infty=\sup_{n\in\N}|u_n|\text{.}\)

On s'intéresse à l'application suivante:

\begin{equation*} L:(u_n)_n\in E\mapsto \lim_{n\rightarrow\infty} u_n\in\R \end{equation*}

(a)

Montrer que la norme \(\|.\|_\infty\) est bien définie sur \(E\text{.}\)

(b)

Montrer que \(L\) est une forme linéaire.

Spoiler.

\(L\) est une application linéaire: soient \((u_n)_n,(v_n)_n\in E\) et \(\lambda,\mu\in\R\text{,}\) on a

\begin{align*} L(\lambda (u_n)_n+\mu (v_n)_n)\amp=L((\lambda u_n + \mu v_n)_n)=\lim_{n\rightarrow\infty} (\lambda u_n + \mu v_n)\\ \amp= \lambda \lim_{n\rightarrow\infty} u_n + \mu \lim_{n\rightarrow\infty} v_n\\ \amp=\lambda L((u_n)_n)+ \mu L((v_n)_n) \end{align*}

Donc \(L\) est linéaire et à valeurs dans \(\R\text{,}\) c'est bien une forme linéaire.

(c)

On munit comme toujours \(\R\) de la norme \(|.|\text{.}\) Montrer que \(L\) est continue et majorer sa norme.

Spoiler.

Montrons que \(L\) est continue. Soit \((u_n)_n\in E\text{,}\) on a \(|L((u_n)_n)| =| \lim_{n\rightarrow\infty} u_n |\text{.}\) Or, pour tout \(n\in\N\text{,}\)

\begin{equation*} |u_n|\leq \sup_{n\in\N}|u_n|=\|(u_n)_n\|_\infty. \end{equation*}

Donc, par passage à la limite dans les inégalités larges,

\begin{equation*} |L((u_n)_n)|=|\lim u_n |\leq \|(u_n)_n\|_\infty \end{equation*}

On en déduit que \(L\) est continue et que \(\|L\|_{\mathcal L(E,\R)} \leq 1\text{.}\)

(d)

Montrer que \(\|L\|_{\mathcal L(E,\R)}=1\text{.}\)

Indice.

Considérer la suite constante égale à 1.

Spoiler.

Reste à montrer que \(\|L\|_{\mathcal L(E)} \geq 1\text{.}\)

Pour cela, considérons la suite \((c_n)_n\) définie, pour tout \(n\in\N\text{,}\) par \(c_n=1\text{.}\) Alors \((c_n)_n\in E\) puisque \((c_n)_n\) est convergente.

De plus, \(\|(c_n)_n\|_\infty = \sup_n |c_n|=\sup_n 1 = 1\text{.}\)

Et d'autre part, \(L((c_n)_n)=\lim c_n =1\text{,}\) donc \(|L((c_n)_n)|=1\text{.}\)

Du coup,

\begin{equation*} \|L\|_{\mathcal L(E,\R)} = \sup_{\|(u_n)_n\|_\infty = 1} |L((u_n)_n)|\geq |L((c_n)_n)| = 1. \end{equation*}

Exercice 8.4.

On considère l'espace vectoriel \(\ell^\infty\) des suites réelles convergentes:

\begin{equation*} \ell^\infty=\{(a_n)_n \in \R^\N, \exists M\geq 0,\forall n\in\N |a_n|\leq M \} \end{equation*}

muni de la norme \(\|(u_n)_n\|_\infty=\sup_{n\in\N}|u_n|\text{.}\) Soit \((b_n)_n\in\ell^\infty\) une suite bornée.

On s'intéresse à l'application suivante:

\begin{equation*} L:(u_n)_n\in \ell^\infty\mapsto (u_n b_n)_n \end{equation*}

(a)

Montrer que \(L\) est un endormorphisme de \(\ell^\infty\text{.}\)

Spoiler.

Montrons que, pour tout \((u_n)\in E\text{,}\) \(L((u_n)_n)\in \ell^\infty\text{.}\) On a

\begin{equation*} \forall n\in \N, |u_nb_n| = |u_n| |b_n|\leq \|(u_n)_n\|_\infty \|(b_n)_n\|_\infty \end{equation*}

\(\leadsto\) La suite \(L((u_n)_n)\) est bornée, donc appartient à \(E\text{.}\)

Montrons que \(L\) est linéaire.

Soient \((u_n)_n,(v_n)_n\in E\) et \(\lambda,\mu\in\R\text{,}\) on a

\begin{align*} L(\lambda (u_n)_n+\mu (v_n)_n)\amp=L((\lambda u_n + \mu v_n)_n)= ((\lambda u_n + \mu v_n)b_n)_n\\ \amp= \lambda (u_n b_n)_n + \mu (v_n b_n)_n \\ \amp=\lambda L((u_n)_n)+ \mu L((v_n)_n) \end{align*}

Donc \(L\) est linéaire.

(b)

Montrer que \(L\) est continue et majorer sa norme.

Indice.

Remarquer que, pour tout \((u_n)_n\in \ell^\infty\text{,}\) pour tout \(n\text{,}\) \(|u_n b_n| \leq \|b_n\|_\infty|u_n|\text{.}\)

Spoiler.

Montrons que \(L\) est continue. Soit \((u_n)_n\in E\text{,}\) on calcule

\begin{equation*} \|L(u_n)_n\|_\infty = \|(u_n b_n)_n\|_\infty= \sup_{n\in\N} |u_nb_n| \end{equation*}

Or, pour tout \(n\in\N\text{,}\) \(|u_n|\leq \sup_{n\in\N} |u_n|=\|(u_n)_n\|_\infty\text{,}\) \(|b_n|\leq \sup_{n\in\N} |b_n|=\|(b_n)_n\|_\infty\) donc, pour tout \(n\in \N\text{,}\)

\begin{equation*} |u_n b_n| = |u_n||b_n| \leq \|(u_n)_n\|_\infty\|(b_n)_n\|_\infty \end{equation*}

donc \(\|(u_n)_n\|_\infty\|(b_n)_n\|_\infty \) est un majorant de \((|u_n b_n|)_n\text{,}\) donc \(\sup_{n\in\N} |u_nb_n|\leq \|(u_n)_n\|_\infty\|(b_n)_n\|_\infty\text{.}\)

On a donc, pour tout \((u_n)_n\in E\text{,}\) \(\|L((u_n)_n)\|_\infty \leq \|(u_n)_n\|_\infty\|(b_n)_n\|_\infty\text{.}\)

On en déduit que \(L\) est linéaire et que \(\|L\|_{\mathcal L(E)} \leq \|(b_n)_n\|_\infty\text{.}\)

(c)

Montrer que \(\|L\|_{\mathcal L(E)}=\|b_n\|_\infty\text{.}\)

Indice.

Considérer la suite constante égale à 1.

Exercice 8.5.

On note \(E=\mathcal C^0([0,1])\) l'ensemble des fonctions continues \([0,1]\rightarrow \R\text{.}\)

(a)

Justifier que, si \(f\in E\text{,}\) alors \(|f|\) admet un maximum sur \([0,1]\text{.}\)

On note \(\|f\|_\infty =\displaystyle \max_{t\in[0,1]}|f(t)|\text{,}\) et on admet que ceci définit une norme sur \(E\text{.}\)

Spoiler.

(b)

On note \(g\) la fonction \(g(x)=2x^2+1\) et on considère l'application

\begin{equation*} L:f\in E\mapsto fg \end{equation*}

Montrer que \(L\) est un endomorphisme continu de \((E,\|.\|_\infty)\text{.}\)

Spoiler.

(c)

Calculer la norme d'application linéaire de \(L\text{.}\)

Spoiler.

Exercice 8.6.

On note \(E=\mathcal C^0([0,1])\) l'ensemble des fonctions continues \([0,1]\rightarrow \R\text{.}\)

(a)

Justifier que, si \(f\in E\text{,}\) alors \(|f|\) admet un maximum sur \([0,1]\text{.}\)

On note \(\|f\|_\infty =\displaystyle \max_{t\in[0,1]}|f(t)|\text{,}\) et on admet que ceci définit une norme sur \(E\text{.}\)

Spoiler.

(b)

On note \(g\) la fonction \(g(x)=3\exp(x)\) et on considère l'application

\begin{equation*} L:f\in E\mapsto fg \end{equation*}

Montrer que \(L\) est un endomorphisme continu de \((E,\|.\|_\infty)\text{.}\)

Spoiler.

(c)

Calculer la norme d'application linéaire de \(L\text{.}\)

www.math3ma.com/blog/operator-norm-intuitively

même si \(F\) est de dimension infinie !