Section 1.1 Comment intégrer ?
Peut-on alors développer une méthode qui s'applique, sinon à tous, au moins à un grand nombre de cas ? C'est là que l'on passe dans le domaine de l'analyse et plus spécifiquement de la théorie de l'intégration.
On reformule la question: étant donnée une fonction \(f:I \rightarrow \mathbb R\) (autrement dit, une quantité qui varie en fonction d'une autre), comment calculer l'aire comprise entre la courbe de \(f\) et l'intervalle \(I\) sur l'axe des abscisses ?
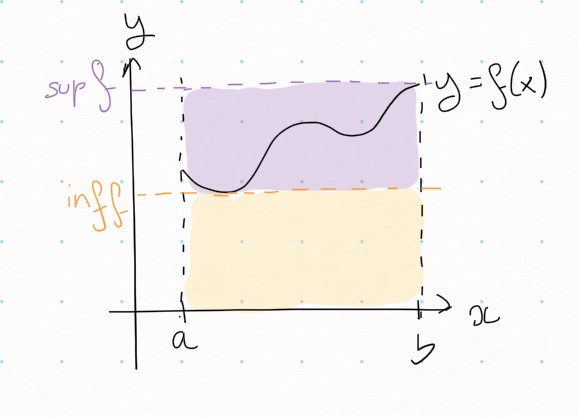
En grossissant suffisamment le trait, on s'aperçoit que l'analyse propose une méthode identique pour une immense variété de problèmes: approximer par quelque chose de plus simple, puis passer à la limite. Dans le cas du calcul d'aire, le plus simple, ce sont les rectangles (c'est-à-dire, les fonctions constantes). On commence donc par approcher la fonction \(f\) par une fonction constante: raisonnablement, celle qui approche le mieux \(f\text{,}\) soit par en-dessous (\(\inf_I f\)), soit par au-dessus (\(\sup_I f\)).
Evidemment, cette approximation est trop grossière pour être satisfaisante. On va donc l'améliorer pas à pas, dans l'idée que, à l'infini, on obtiendra l'aire souhaitée. Pour faire mieux, donc, on peut découper \(I\) en deux sous-intervalles \(I_1\) et \(I_2\text{,}\) et approcher \(f\) par une constante sur chaque sous-intervalle. Pour faire encore mieux que ça, on peut redécouper \(I_1\) et \(I_2\text{.}\) Et ainsi de suite...
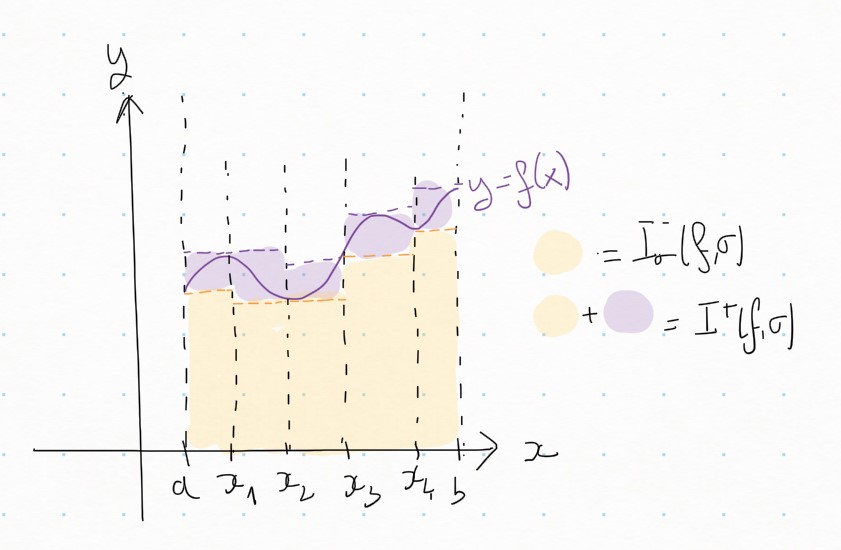
Un précurseur de cette solution se trouve déjà dans le cours d'analyse de Cauchy, rédigé en 1821. Dans ce cours, si \(f:\rbb a,b\lbb \rightarrow \mathbb R\) est une fonction continue, alors on lui associe son intégrale \(I(f)\) par
Remarque 1.1.3.
Dans cette formule, sur chaque sous-intervalle
\(f\) est approximée par la fonction constante égale à \(f(a+k\frac{b-a}N)\text{,}\) plutôt que par \(\inf_{\lbb a+k\frac{b-a}N,a+(k+1)\frac{b-a}N \rbb } f\) ou \(\sup_{\lbb a+k\frac{b-a}N,a+(k+1)\frac{b-a}N\rbb} f\text{.}\) S'agissant d'une fonction continue, on obtient la même limite quand \(N\rightarrow \infty\) 1
Les travaux de Riemann, présentés vers 1850, visaient à déterminer pour quelles fonctions (au-delà des fonctions continues) on pouvait faire fonctionner ce procédé.