Section 3.2 Tribus et ensembles mesurables
Cela nous amène à la définition suivante:
Définition 3.2.1.
Soit \(X\) un ensemble. On appelle tribu (ou \(\sigma\)-algèbre) sur \(X\) une famille \(\mathscr T\) de parties de \(X\) telle que
\(\displaystyle \emptyset \in \mathscr T\)
Si \(A\in \mathscr T\) alors son complémentaire \(A^c\in \mathscr T\)
Si \((A_n)_n \) est une famille dénombrable d'éléments de \(\mathscr T\text{,}\) alors \(\bigcup_n A_n \in \mathscr T\text{.}\)
Les éléments de \(\mathscr T\) sont les parties mesurables de \(X\text{,}\) et on dit que \((X, \mathscr T)\) est un espace mesurable.
Quelques propriétés immédiates qui découlent de cette définition:
Proposition 3.2.2.
Soit \(\mathscr T\) une tribu sur \(X\text{.}\) Alors
\(\displaystyle X \in \mathscr T\)
\(\mathscr T\) est stable par intersection dénombrable: si \((A_n)_n \) est une famille dénombrable d'éléments de \(\mathscr T\text{,}\) alors \(\bigcap_n A_n \in \mathscr T\text{.}\)
Pour tous \(A, B \in \mathscr T\text{,}\) \(A \cup B\text{,}\) \(A \cap B\text{,}\) \(A \setminus B\) appartiennent aussi à \(\mathscr T\text{.}\)
Exemple 3.2.3.
Les exemples suivants fonctionnent quel que soit l'ensemble \(X\text{:}\)
\(\{\emptyset, X\}\) est la plus petite tribu sur \(X\text{.}\)
Soit \(A \subset X\text{.}\) Alors \(\{\emptyset, A, A^c, X\}\) est la plus petite tribu sur \(X\) qui contient \(A\text{.}\)
\(\mathcal P(X)\) est la plus grande tribu sur \(X\text{.}\)
\(\{A \in \mathcal P(X),\, A \text{ dénombrable ou } A^c \text{ dénombrable }\}\) est une tribu sur \(X\text{.}\)
Exemple 3.2.4. Contre-exemple.
Soit \((E, \|.\|)\) un espace vectoriel normé. Alors l'ensemble des ouverts de \(E\) n'est pas une tribu, puisque le complémentaire d'un ouvert est un fermé (en général non ouvert).
L'ensemble des ouverts et des fermés de \(E\) n'est toujours pas une tribu: par exemple, dans \(\mathbb R\text{,}\) pour tout \(n\text{,}\) \(\rbb 0,1-\frac 1n\lbb \) est fermé, mais \(\bigcup_n \rbb 0,1-\frac 1n\lbb = \rbb 0,1\rbb \) n'est ni ouvert, ni fermé.
Et re-exemples:
Petit Exercice 3.2.5. Exemple 1.
Soit \(X\) un ensemble non vide, et \(A\in\mathcal P(X)\) un sous-ensemble de \(X\text{.}\) Montrer que
est une tribu sur \(X\text{.}\)
Petit Exercice 3.2.6. Exemple 2.
Soit \(X\) un ensemble non vide. Montrer que l'ensemble
est une tribu sur \(X\text{.}\)
Petit Exercice 3.2.7. Exemple 3.
Montrer que l'ensemble
des sous-ensembles de \(\mathbb R\) symétriques par rapport à 0 est une tribu sur \(\mathbb R\text{.}\)
Petit Exercice 3.2.8. Exemple 4:.
Soit \(X\) un ensemble non vide, et \(\mathscr T\) une tribu sur \(X\text{.}\) Soit de plus \(A\subset X\text{.}\) Montrer que l'ensemble
est une tribu sur \(X\text{.}\)
Subsection 3.2.1 Fabrication de tribus
A partir d'une tribu \(\T\) sur un ensemble \(X\text{,}\) on peut en construire de nouvelles:
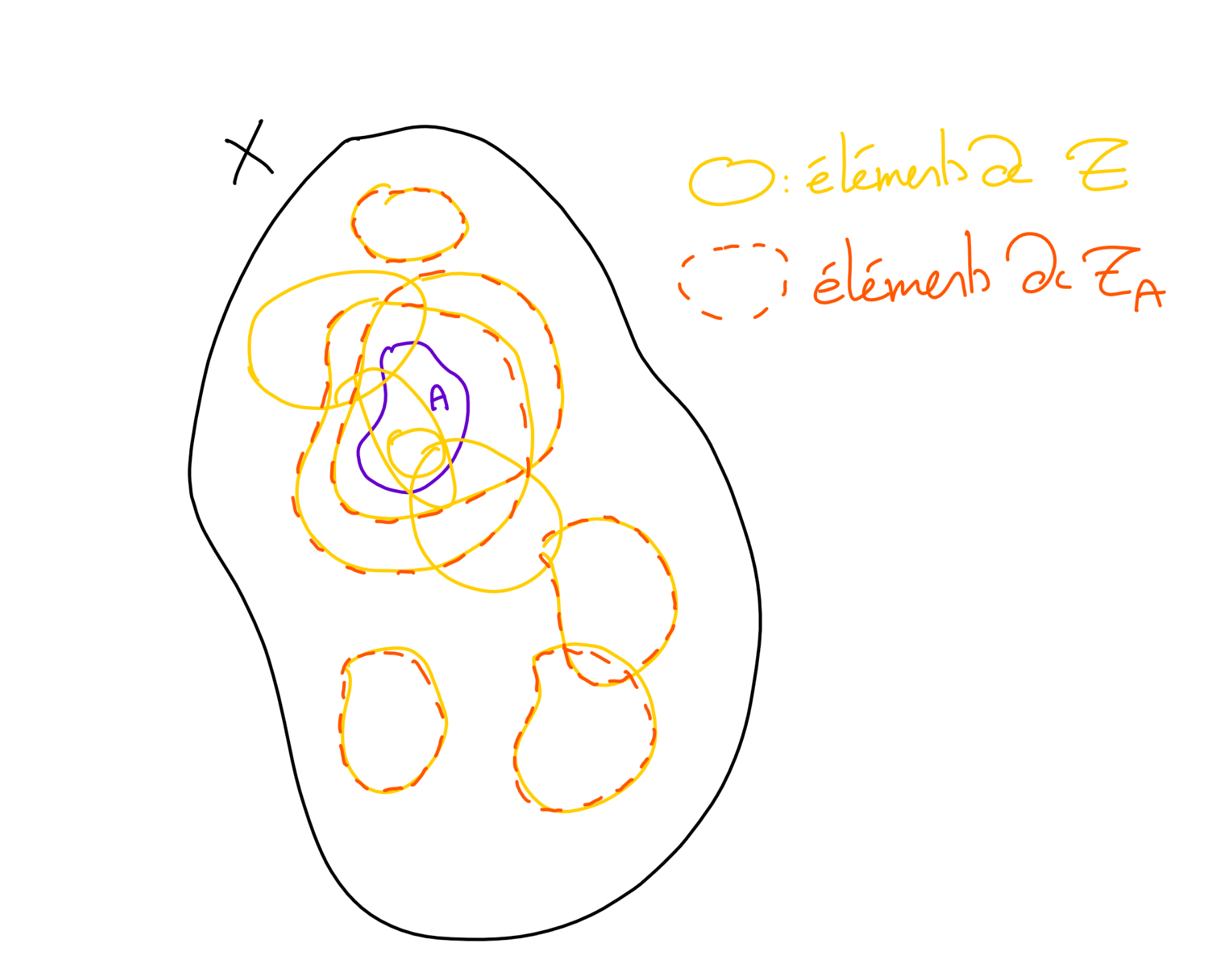
Proposition 3.2.9. Tribu-trace.
Soit \((X,\T)\) un ensemble mesurable, et soit \(A\subset X\) un sous-ensemble (mesurable ou non). On note
Alors \(\T_A\) est une tribu sur \(A\text{,}\) qu'on appelle la tribu-trace de \(\T\) sur \(A\text{.}\)
Petit Exercice 3.2.10.

Proposition 3.2.11. Tribu-image réciproque.
Soit \((Y,\S)\) un ensemble mesurable, \(X\) un autre ensemble et \(f:X\rightarrow Y\) une fonction.
Alors \(f^{-1}(\S)\) est une tribu sur \(X\text{,}\) qu'on appelle la tribu-image réciproque de \(\S\) sur \(f\text{.}\)
Petit Exercice 3.2.12.

Petit Exercice 3.2.13. Lien avec la tribu-trace.
Soit \((X,\T)\) un ensemble mesurable, et soit \(A\subset X\text{.}\) On note
la fonction inclusion de \(A\) dans \(X\text{.}\) Montrer que
autrement dit la tribu trace de \(\T\) sur \(A\) coincide avec la tribu image réciproque de \(\T\) par \(i_A\text{.}\)
En revanche, si \((X,\T)\) est un ensemble mesurable, \(Y\) un autre ensemble et \(f:X\rightarrow Y\) une fonction, alors en général, la famille de sous-ensembles
n'est pas une tribu sur \(Y\text{.}\)
C'est assez facile à voir, en fait: considérons un exemple mesuré simple: \(X=\{1,2,3\}\) avec la tribu \(\mathcal P(X)\text{,}\) \(Y=\{Chocolat, Epinard, Salsifi\}\text{.}\) On prend une fonction constante
Alors que que soit \(A\in\P(X)\) non vide,
et
donc \(\{f(A),A\in \T\} = \{\, \{Chocolat\}\, \}\) n'est pas une tribu, puisque \(Y\notin \{Chocolat\}\, \}\text{.}\)
Petit Exercice 3.2.14.
Trouver un contre-exemple où \(f\) est surjective.
Prenons
avec la tribu sur \(X\text{:}\)
et la fonction \(f:X\rightarrow Y\) définie par
Alors
n'est pas stable par complémentaire, donc ce n'est pas une tribu sur \(Y\text{.}\)
Du coup, pour passer d'une tribu sur \(X\) à une tribu sur \(Y\) via une fonction \(f:X\rightarrow Y\text{,}\) il faut se contorsionner un peu:
Proposition 3.2.15. Tribu-image.
\((X,\T)\) est un ensemble mesurable, \(Y\) un autre ensemble et \(f:X\rightarrow Y\) une fonction. On note
Alors \(f(\T)\) est une tribu sur \(Y\text{,}\) qu'on appelle la tribu-image de \(\T\) sur \(f\text{.}\)
Petit Exercice 3.2.16.

Exemple 3.2.17.
Si on reprend
avec la tribu sur \(X\text{:}\)
et la fonction \(f:X\rightarrow Y\) définie par
alors
ce qui donne
donc au total,
\(\leadsto\) C'est bien une tribu sur \(Y\) (quoi que pas très riche, mais bon, \(Y\) lui-même est assez peu intéressant...sauf si on parle de loi de Bernoulli, peut-être).