Skip to main content

Section 1.2 Construction de l'intégrale de Riemann

Formalisons cette idée. Tout d'abord, identifions les cas simples: ce sont les fonctions constantes, ou, au pire, constantes par morceaux. On pose donc:

Définition 1.2.1.

Une fonction \(f:\rbb a,b\lbb \rightarrow \mathbb R\) est en escaliers s'il existe une subdivision \(\sigma=(a=t_0 \lt t_1 \lt \dots \lt t_n=b)\) de \(\rbb a,b\lbb \) en \(n\) sous-intervalles \(\lbb t_i,t_{i+1}\rbb \) et des réels \(\lambda_0, \dots, \lambda_{n-1}\) tels que

\begin{equation*} f = \sum_{i=0}^{n-1} \mathbb{1}_{\lbb t_i,t_{i+1}\rbb } = \lambda_i. \end{equation*}

On note \(\mathcal E(\rbb a,b\lbb )\) l'ensemble des fonctions en escalier sur \(\rbb a,b\lbb \text{.}\)

L'intégrale d'une telle fonction est une somme d'aires de rectangles:

Définition 1.2.2.

Soit \(f \in \mathcal E(\rbb a,b\lbb )\) une fonction en escalier. Son intégrale sur \(\rbb a,b\lbb \) est définie par

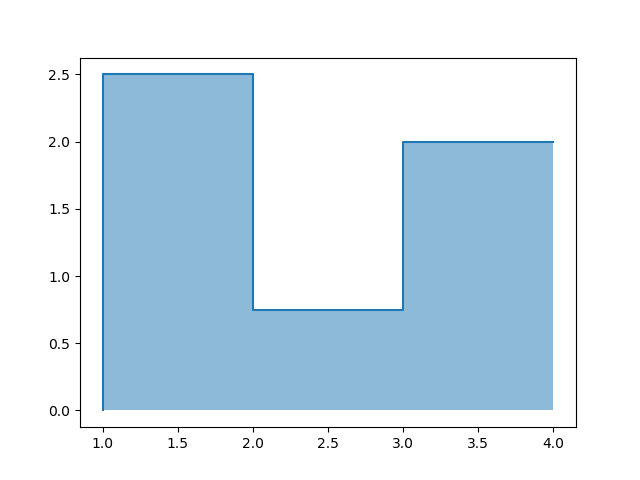
\begin{equation*} I(f)= \sum_{i=0}^{n-1} \underbrace{(t_{i+1}-t_i)}_{\text{base}} \cdot \underbrace{\lambda_i}_{\text{hauteur}}. \end{equation*}
Figure 1.2.3. Intégrale des fonctions en escalier

Passons maintenant au cas général. Soit \(f: \rbb a,b\lbb \rightarrow \mathbb R\) une fonction bornée, et \(\sigma=(a=t_0 \lt x_1 \lt \dots \lt t_n=b)\) une subdivision de l'intervalle \(\rbb a,b\lbb \) en sous-intervalles \(\rbb t_i,t_{i+1}\lbb \text{.}\) Sur chaque sous-intervalle, on approche \(f\) par une fonction constante.

  • On peut choisir \(\sup_{\rbb t_i,t_{i+1}\lbb } f\text{:}\) on approche \(f\) par la fonction en escalier

    \begin{equation*} h_\sigma^+ = \sum_{i=0}^{n-1}\sup_{\rbb t_i,t_{i+1}\lbb } f\cdot \mathbb{1}_{\rbb t_i,t_{i+1}\rbb } \end{equation*}

  • On peut aussi prendre \(\inf_{\rbb t_i,t_{i+1}\lbb } f\) : on approche \(f\) par la fonction en escalier

    \begin{equation*} h_\sigma^- = \sum_{i=0}^{n-1}\inf_{\rbb t_i,t_{i+1}\lbb } f \cdot \mathbb{1}_{\rbb t_i,t_{i+1}\rbb }. \end{equation*}

Remarque 1.2.4.

Il y a en fait beaucoup de choix possibles à ce stade: on peut aussi prendre \(f(t_i)\) (méthode des rectangles à gauche), \(f(t_{i+1})\) (méthode des rectangles à droite), \(f\left(\frac{t_i+t_{i+1}}2\right)\) (méthode du point milieu)... Si \(f\) est une fonction "sympathique", tout cela devrait donner le même résultat. L'intérêt de choisir le sup et l'inf est de déterminer si la fonction est suffisamment sympathique.

On approche donc l'aire sous la courbe de \(f\) par l'intégrale de ces fonctions en escalier:

\begin{equation*} I^+(f,\sigma) = \sum_{i=0}^{n-1} (t_{i+1}-t_i) \sup_{\rbb t_i,t_{i+1}\lbb } f, \quad I^-(f,\sigma) =\sum_{i=0}^{n-1} (t_{i+1}-t_i) \inf_{\rbb t_i,t_{i+1}\lbb } f \end{equation*}

où \(I^+(f,\sigma)\) est légèrement plus grande que l'aire sous la courbe de \(f\) et \(I^-(f,\sigma)\) est légèrement plus petite. Si on prend des subdivisions de plus en plus fines (et que \(f\) n'est pas trop méchante), on devrait approcher de mieux en mieux l'aire sous la courbe de \(f\text{.}\) On définit donc

\begin{equation*} \begin{cases} I^+(f) = \inf \{ I^+(f,\sigma)\,|\, \sigma \text{ subdivision de } \rbb a,b\lbb \},\\ I^-(f) = \sup \{ I^-(f,\sigma)\,|\, \sigma \text{ subdivision de } \rbb a,b\lbb \} \end{cases} \end{equation*}

et on dit que \(f\) est intégrable si \(I^+(f) = I^-(f)\text{.}\) Dans ce cas, on appelle cette quantité l'intégrale de \(f\) sur \(\rbb a,b\lbb \text{,}\) notée \(\int_a^b f(t)dt\text{.}\) Les fonctions intégrables incluent les fonctions continues, les fonctions monotones, et bien sûr les fonctions en escaliers.

\(\leadsto\)une illustration interactive. 1 

En déroulant les définitions de sup et inf, on obtient le critère d'intégrabilité suivant:

L'intégrale de Riemann a les propriétés qu'on attend intuitivement de "l'aire sous la courbe": linéarité, monotonie, relation de Chasles. Dans le cas des fonctions continues, le calcul explicite d'intégrales est grandement facilité par le lien entre intégrale et primitives:

Une version animée:

Toutefois, son champ d'application est limité aux fonctions bornées sur un intervalle borné.

On peut contourner ce problème, et étendre la notion d'intégrale à des fonctions définies sur des intervalles ouverts éventuellement infinis. Ce sont les intégrales impropres, et elles sont définies par passage à la limite (évidemment).

Définition 1.2.7. Intégrales impropres.

  • Soit \(f:\rbb a, b\rbb \rightarrow \mathbb R\text{,}\) où \(b \in \mathbb R \cup \{+\infty\}\text{.}\) On dit que \(f\) est localement intégrable sur \(\rbb a,b\rbb \) si, pour tout \(x\lt b\text{,}\) \(f\) est Riemann-intégrable sur \(\rbb a,x\lbb \text{.}\)

  • Soit \(f\) une fonction localement intégrable sur \(\rbb a,b\rbb \text{.}\) Si \(\lim_{x\rightarrow b} \int_a^x f(t)dt\) existe, on dit que l'intégrale généralisée \(\int_a^b f(t)dt\) converge. Sinon, on dit qu'elle diverge.

Remarque 1.2.8.

On n'est bien sûr pas limités aux intervalles ouverts à droite:

  1. On définit de même les fonctions localement intégrables sur \(\lbb a,b\lbb \text{,}\) où \(a\in \mathbb R \cup \{-\infty\}\text{,}\) et leurs intégrales généralisées.

  2. Si \(f: \lbb a,b\rbb \rightarrow \mathbb R\) est localement intégrable, on dit que son intégrale généralisée \(\int_a^bf(t) dt\) converge si, et seulement si, pour \(c\in \lbb a,b\rbb \text{,}\) les deux intégrales généralisées \(\int_a^c f(t) dt\) et \(\int_c^b f(t) dt\) convergent.

Vous l'aurez remarqué, l'analyste aime les limites. Il serait donc assez naturel que, si une suite de fonctions \((f_n)_n\) converge en chaque point vers une fonction \(f\text{,}\) alors l'aire sous la courbe de \(f_n\) converge vers l'intégrale de \(f\text{.}\) En fait, c'est par une procédé de ce genre qu'on a obtenu l'intégrale ! Cependant, pour échanger limite et intégrale, il nous faut en fait une version plus restrictive de la simple convergence en chaque point.

Définition 1.2.9.

Soit \(f:\rbb a,b\lbb \rightarrow \mathbb R\) une fonction, et \((f_n)_n\) une suite de fonctions sur \(\rbb a,b\lbb \text{.}\) On dit que la suite \((f_n)_n\) converge uniformément vers \(f\) sur \(\rbb a,b\lbb \) si

\begin{equation*} \sup_{x \in \rbb a,b\lbb } |f_n(x) - f(x)| \xrightarrow[n\rightarrow \infty]{} 0 \end{equation*}

Avec cette notion renforcée de convergence, on obtient:

et, pour les intégrales généralisées:

mybinder.org/v2/gh/cvernier0/series_bertrand/master?filepath=Riemann.ipynb