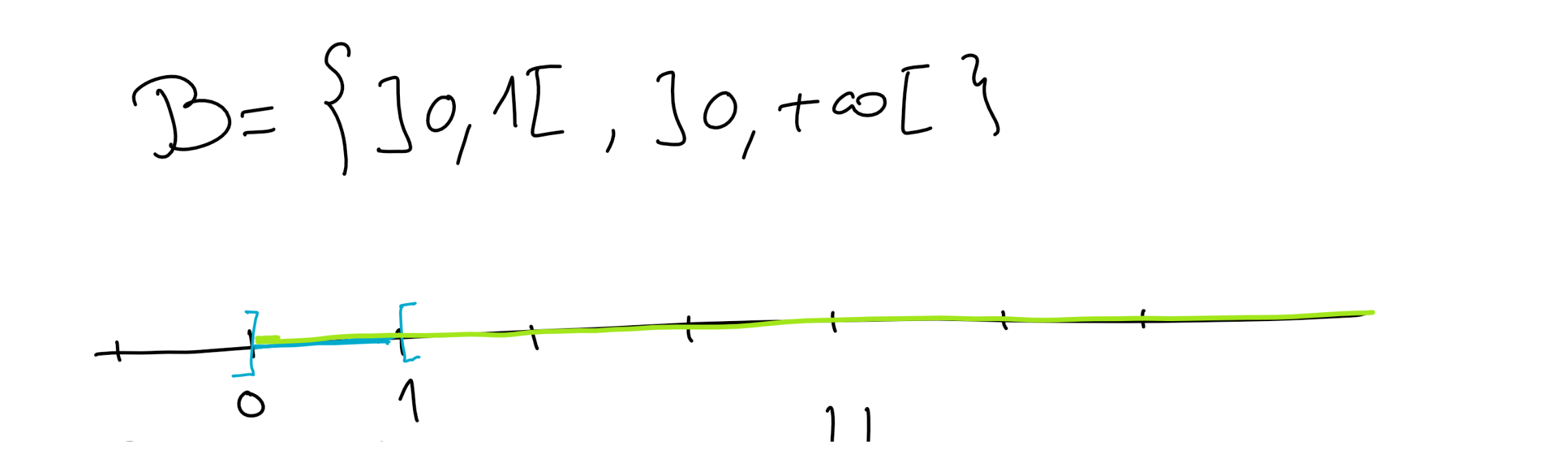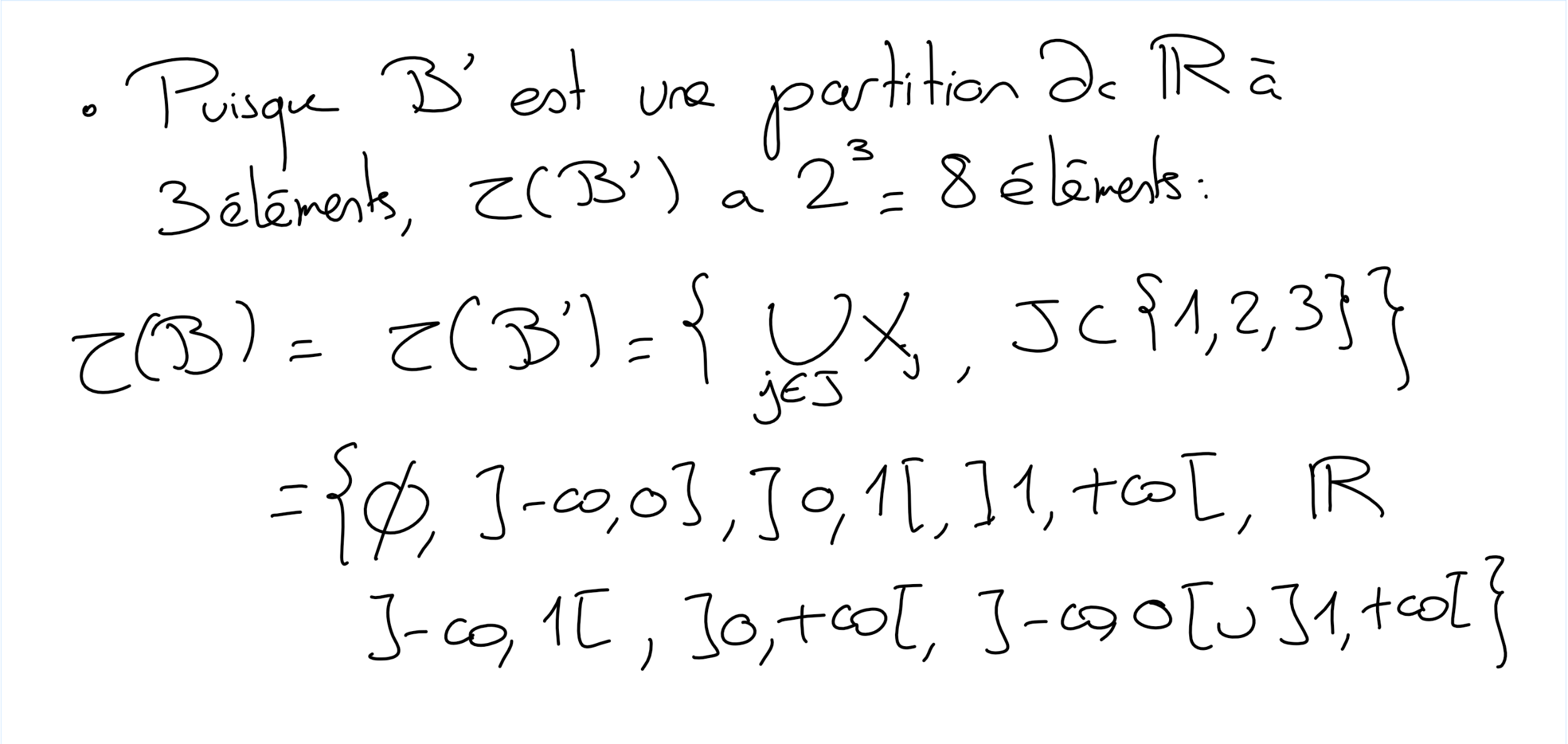Skip to main content

Section 3.2 Tribu engendrée

On a trouvé tout un tas d'exemples de tribus sur un ensemble \(X\text{,}\) cela ne nous avance pas beaucoup dans notre recherche des sous-ensembres mesurables sur \(\R\text{:}\) on a eu l'idée d'élargir notre champ de recherche aux ouverts de \(\R\) (et donc aux fermés, par passage au complémentaire), mais on a vu que, pour un e.v.n. \(E\) quelconque, la famille

\begin{equation*} \mathcal O \cup \mathcal F=\{A\in\mathcal P(E),\ A \text{ ouvert ou } A \text{ fermé}\} \end{equation*}

n'est pas une tribu.

Pour se sortir de là, on voudrait partir d'une famille \(\mathcal F\) d'ensembles intéressants, par exemple la famille des ouverts ou celle des intervalles, qui n'est pas une tribu, et lui ajouter tout ce qui lui manque pour en être une, mais pas plus  1 .

Pour ça, on va prendre toutes les tribus possibles qui contiennent \(\mathcal F\) (même si on ne les connaît pas), et ne garder que ce qu'elles ont de commun:

Exercice 3.2.1. Preuve.

On vérifie que \(\sigma(\mathcal F)\) vérifie les axiomes des tribus:

(a)

Montrer que \(X\in \sigma(\mathcal F)\text{.}\)

Spoiler.

Pour toute tribu \(\mathsrc T\) telle que \(\mathcal F \subset \mathscr T\text{,}\) on a \(X \in \mathscr T\text{,}\) puisque \(\mathscr T\) est une tribu.

Donc \(\emptyset \in \sigma(\mathcal F)\) \(\checkmark\text{.}\)

(b)

Montrer que, pour tout \(A \in \sigma(\mathcal F)\text{,}\) \(A^c \in \sigma(\mathcal F)\text{.}\)

Spoiler.

Soit \(A \in \sigma(\mathcal F)\text{,}\) et soit \(\mathscr T\) une tribu telle que \(\mathcal F \subset \mathscr T\text{.}\)

Alors \(A \in \mathscr T\text{,}\) donc,, puisque \(\mathscr T\) est une tribu, \(A^c \in \mathscr T\text{.}\)

Ceci étant vrai pour toute tribu \(\mathscr T\) contenant \(\mathcal F\text{,}\) on a bien \(A^c\in \sigma( \mathcal F)\text{.}\)

(c)

Montrer que, pour toute suite \((A_n)_n \in \sigma(\mathcal F)^\mathbb N\text{,}\) \(\bigcup A_n \in \sigma( \mathcal F)\text{.}\)

Spoiler.

De même, soit \((A_n)_n \in \sigma(\mathcal F)^\mathbb N\text{,}\) et soit \(\mathscr T\) une tribu telle que \(\mathcal F \subset \mathscr T\text{.}\)

Alors, pour tout \(n\in \mathbb N\text{,}\) \(A_n \in \mathscr T\text{,}\) donc \(\bigcup A_n \in \mathscr T\text{.}\)

Ceci étant vrai pour toute tribu \(\mathscr T\) contenant \(\mathcal F\text{,}\) on a bien \(\bigcup A_n \in \sigma( \mathcal F)\text{.}\)

Remarque 3.2.4.

Méthode: Pour montrer que \(\tau(\mathscr A)=\mathscr S\text{,}\) on procède par double inclusion:

  • \(\boxed{\subset}\) On montre que \(\mathscr S\) est une tribu qui contient \(\mathscr A\text{.}\) Puisque \(\tau(\mathscr A)\) est la plus petite tribu qui contient \(\mathscr A\text{,}\) on a donc \(\tau(\mathscr A)\subset\mathscr S\text{.}\)

  • \(\boxed{\supset}\) On montre que toute tribu qui contient \(\mathscr A\) doit aussi contenir \(\mathscr S\) (en général, en utilisant le fait que les éléments de \(\mathscr S\) sont des unions ou intersections dénombrables, ou encore complémentaires, d'éléments de \(\mathscr A\text{.}\) On a alors

    \begin{gather*} \forall \mathscr T \text{ tribu t.q. } \mathscr A\subset\mathscr T, \mathscr S\subset\mathscr T\\ \text{ donc } \mathscr S \subset \bigcap_{\substack{\mathscr T \text{ tribu} \\ \mathscr A\subset\mathscr T}}\mathscr T=\tau(\mathscr A) \end{gather*}

Exercice 3.2.2. Exemples.

(a)

Dans \(X= \mathbb R\text{,}\) considérons par exemple \(\mathcal F = \{\lbb 0,1\rbb ,\, \lbb 0,\infty\rbb \}\text{.}\) Montrer que

\begin{equation*} \sigma(\mathcal F) = \{\emptyset, \lbb 0,1\rbb ,\, \lbb 0,\infty\rbb , \lbb -\infty, 0\lbb , \rbb 1, \infty\rbb , \lbb -\infty, 0\lbb \cup \rbb 1, \infty\rbb , \lbb -\infty, 1\rbb , \mathbb R \}. \end{equation*}

Exercice 3.2.3. Exemples.

(a)

Déterminer \(\sigma(\emptyset)\) et \(\sigma(\{\emptyset\})\text{.}\)

En déduire qu'une même tribu peut être engendrée par plusieurs familles différentes.

(b)

Soit \(X\) un ensemble et \(A\subset X\text{.}\) Montrer que la tribu

\begin{equation*} \mathscr T_1=\{\emptyset, A, A^c, X\} \end{equation*}

qu'on avait définie l' Exercice 3.1.1 est engendrée par \(\{A\}\subset \mathcal P(X)\text{:}\)

\begin{equation*} \mathscr T_1=\sigma(\{A\}) = \sigma(\{A^c\}). \end{equation*}
Spoiler.

On a déjà croisé cette idée à l'Exercice 3.1.1, mais reformulons-la à l'aide de notre nouvelle notion de tribu engendrée:

(c)

Considérons la famille de parties de \(\mathbb Z\) suivante:

\begin{equation*} \mathscr A=\left\{\{n,n+1,n+2\}, n\in \mathbb Z\right\}\subset \mathcal P(\mathbb Z). \end{equation*}

Montrer que

\begin{equation*} \tau(\mathscr A) = P(\mathbb Z) \end{equation*}
Spoiler.

Exercice 3.2.4. Tribus engendrées par les sous-ensembles finis.

A a fin de l'Exercice 3.1.1, on a introduit la tribu

\begin{equation*} \mathscr T_2 =\{E\subset X, E \text{ au plus dénombrable ou } E^c \text{ au plus dénombrable }\} \end{equation*}

On va voir qu'elle admet tout un tas de familles génératrices, incluant notamment les familles des sous-ensembles finis de différents cardinaux.

(a)

Soit \(X\) un ensemble, et \(\mathscr S\) la famille de tous les singletons de \(X\text{:}\)

\begin{equation*} \mathscr S = \{\{x\}, x\in X\}\subset \mathcal P(X) \end{equation*}

Montrer que la tribu

définie à l est engendrée par \(\mathscr S\text{.}\)

Indice.

Un singleton est un ensemble au plus dénombrable.

Et un ensemble au plus dénombrable \(E\) de \(X\) est une union au plus dénombrable de singletons:

\begin{equation*} E=\bigcup_{x\in E} \{x\} \end{equation*}
Spoiler.

(b)

On suppose que \(X\) a au moins 3 éléments distincts. Considérons maintenant la famille \(\mathscr B\) des sous-ensembles de \(X\) à deux éléments:

\begin{equation*} \mathscr B = \{\{x,y\}, x,y\in X\}\subset \mathcal P(X) \end{equation*}

Montrer que

\begin{equation*} \mathscr T_2=\tau(\mathscr B). \end{equation*}
Indice.

Utiliser la question précédente: montrer que si \(\{x\}\in\mathscr S\) alors \(\{x\}\in \tau(\mathscr B)\) (en l'écrivant comme intersection d'éléments de \(\mathscr B\text{:}\) c'est là qu'il va être utile d'avoir au moins trois éléments différents).

Spoiler.

(c)

Allons plus loin. On maintenant suppose que \(X\) est infini. et on considère la famille \(\mathscr B_n\) des sous-ensembles de \(X\) à \(n\) éléments:

\begin{equation*} \mathscr B_n = \{\{x_1,\ldots,x_n\}, x_i\in X\}\subset \mathcal P(X) \end{equation*}

Montrer que

\begin{equation*} \forall n\in \mathbb N^*,\ \mathscr T_2=\tau(\mathscr B_n). \end{equation*}
Indice.

Utiliser la méthode de la question précédente pour faire marcher un raisonnement par récurrence.

Spoiler.

Exercice 3.2.5. Tribu engendrée par une partition de \(X\).

(a)

Montrer que la famille de parties de \(\mathbb R\) définie par:

\begin{equation*} \mathscr T = \left\{\bigcup_{n\in I} \rbb n,n+1\rbb ,\ I\subset \mathbb Z \right\}\subset \mathcal P(\mathbb R) \end{equation*}

est une tribu de parties de \(\mathbb R\text{.}\)

Indice.
Spoiler.

(b)

Plus généralement, soit \(X\) un ensemble non vide. On considère une partition au plus dénombrable \((X_i)_{i\in I}\) de \(X\text{,}\) autrement dit, \((X_i)_{i\in I}\) est une famille de parties de \(X\) telle que

\begin{equation*} \begin{cases} I \text{ est fini ou dénombrable,}\\ \forall\, i,j\in I \text{ t.q. } i\neq j,\ X_i\cap X_j=\emptyset\\ X=\bigcup_{i\in I}X_i. \end{cases} \end{equation*}

(On suppose de plus, quitte à élaguer, que les \(X_i\) sont non vides)

On définit:

\begin{equation} \mathscr T = \left\{\bigcup_{j\in J}X_j,\ J\subset I\right\}\subset \mathcal P(X)\tag{3.2.1} \end{equation}

Montrer que \(\mathscr T\) est une tribu sur \(X\text{.}\)

Indice.
Ca va ressembler furieusement à la question précédente.
Spoiler.

(c)

Montrer qu'alors la tribu \(\mathscr T\) définie en (3.2.1) est engendrée par les ensembles de la partition:

\begin{equation*} \mathscr T = \tau\left(\{X_i,\ i\in I\}\right) \end{equation*}
Spoiler.

(d)

Supposons que \(I\) est fini. Combien d'éléments y a-t-il dans la tribu \(\mathscr T\) ?
Indice.
Combien y a-t-il de sous ensembles \(J\subset I\) ?
Spoiler.

Considérons l'application:

\begin{align*} \Psi: \mathcal P(I) \amp\rightarrow \mathscr T \\ J\amp \mapsto \bigcup_{j\in J}X_j \end{align*}

Montrons qu'elle est bijective.

  • \(\Psi\) est surjective par définition de \(\mathscr T\text{:}\) pour tout \(A\in\mathscr T\text{,}\) il existe un sous-ensemble \(J\subset I\) tel que \(A= \cup_{j\in J}X_j\text{.}\)

  • \(\Psi\) est injective: si \(J\neq J'\) sont deux sous-ensembles distincts de \(I\text{.}\) Alors soit \(J\setminus J' \neq \emptyset\text{,}\) soit \(J' \setminus J \neq \emptyset\text{.}\) Disons \(J\setminus J' \neq \emptyset\) (l'autre cas est symétrique). Soit donc \(j_0\in J\setminus J'\) et \(x\in X_{j_0}\text{.}\) Alors, puisque les \(X_i,\ i\in I\) sont disjoints, pour tout \(i\neq j_0\text{,}\) \(x\notin X_i\text{.}\) En particulier:

    \begin{equation*} x\in \bigcup_{j\in J}X_j=\Psi(J) \text{ et } x\notin \bigcup_{j\in J'}X_j=\Psi(J') \end{equation*}

    donc \(\Psi(J)\neq \Psi(J')\text{.}\) Donc \(\Psi\) est injective.

Puisque \(\Psi\) réalise une bijection entre \(\mathcal P(I)\) et \(\mathscr T\text{,}\) ces deux ensembles ont le même cardinal, d'où

\begin{equation*} \text{Card}(\mathscr T) = 2^{\text{Card}(I)}. \end{equation*}

(e)

Il est plus facile de trouver la tribu engendrée par une famille finie \(mathscr A\) si cette famille est une partition de \(X\text{:}\) on sait combien d'ensembles la tribu contient, et les intersections et unions sont plus faciles à calculer.

Du coup, en se ramenant à une partition, déterminer sans douleur la tribu sur \(\mathbb R\) engendrée par la famille

\begin{equation*} \mathscr A = \{\rbb 0,2\lbb , \rbb 1,3\lbb \}\text{.} \end{equation*}
Indice.

Trouver une partition \(\mathscr A'=\{X_i, i\in I\}\) de \(\mathbb R\) telle que les \(X_i\) sont dans \(\tau(\mathscr A)\text{:}\) par exemple, des intersections ou complémentaires d'éléments de \(\mathscr A\text{.}\) Puis utiliser les questions précédentes qui décrivent \(\tau(\mathscr A')\text{.}\)

Spoiler.

(f)

Toujours suivant cette ligne de raisonnement, déterminer la tribu sur \(\mathbb R\) engendrée par la famille

\begin{equation*} \mathscr B = \{\lbb 0,1\rbb , \lbb 0,+\infty\rbb \}\text{.} \end{equation*}
Indice.

Même topo: on peut chercher une partition finie \(\mathscr B'\) de \(\mathbb R\) obtenue via des intersections/complémentaires/union d'éléments de \(\mathscr B\text{.}\) Puis utiliser les questions précédentes qui décrivent \(\tau(\mathscr B')\text{.}\)

Spoiler.

(g)

Plus généralement, soit \(X\neq \emptyset\) et soient \(A,B \in \mathcal P(X)\) tels que \(A\subset B\text{.}\) Déterminer \(\tau(\{A,B\})\text{.}\)
Indice.
C'était la situation à l'exemple précédent. Comment généraliser la partition qu'on a utilisée ?
Spoiler.

Subsection 3.2.1 Image réciproque d'une tribu engendrée

On a vu précedemment que, si on a une tribu \(\mathscr S\) sur un ensemble \(Y\) et une fonction \(f:X\rightarrow Y\text{,}\) alors on peut "tirer en arrière" la tribu \(\mathscr S\) à l'aide de la fonction \(f\) pour obtenir une tribu sur \(X\text{:}\) la tribu image réciproque, notée \(f^{-1}(\mathscr S)\text{,}\) de \(\mathscr S\) par \(f\text{.}\)

S'il se trouve qu'on connaît une famille \(\mathscr E\) qui engendre \(\mathscr S\text{,}\) alors on peut aussi tirer en arrière cette famille avec \(f\text{,}\) et ça nous donnera une famille qui engendre \(f^{-1}(\mathscr S)\text{:}\)

Sinon, on peut toujours prendre la tribu \(\P(X)\) qui contient tous les sous-ensembles...mais on a vu que ça ne marchait pas.