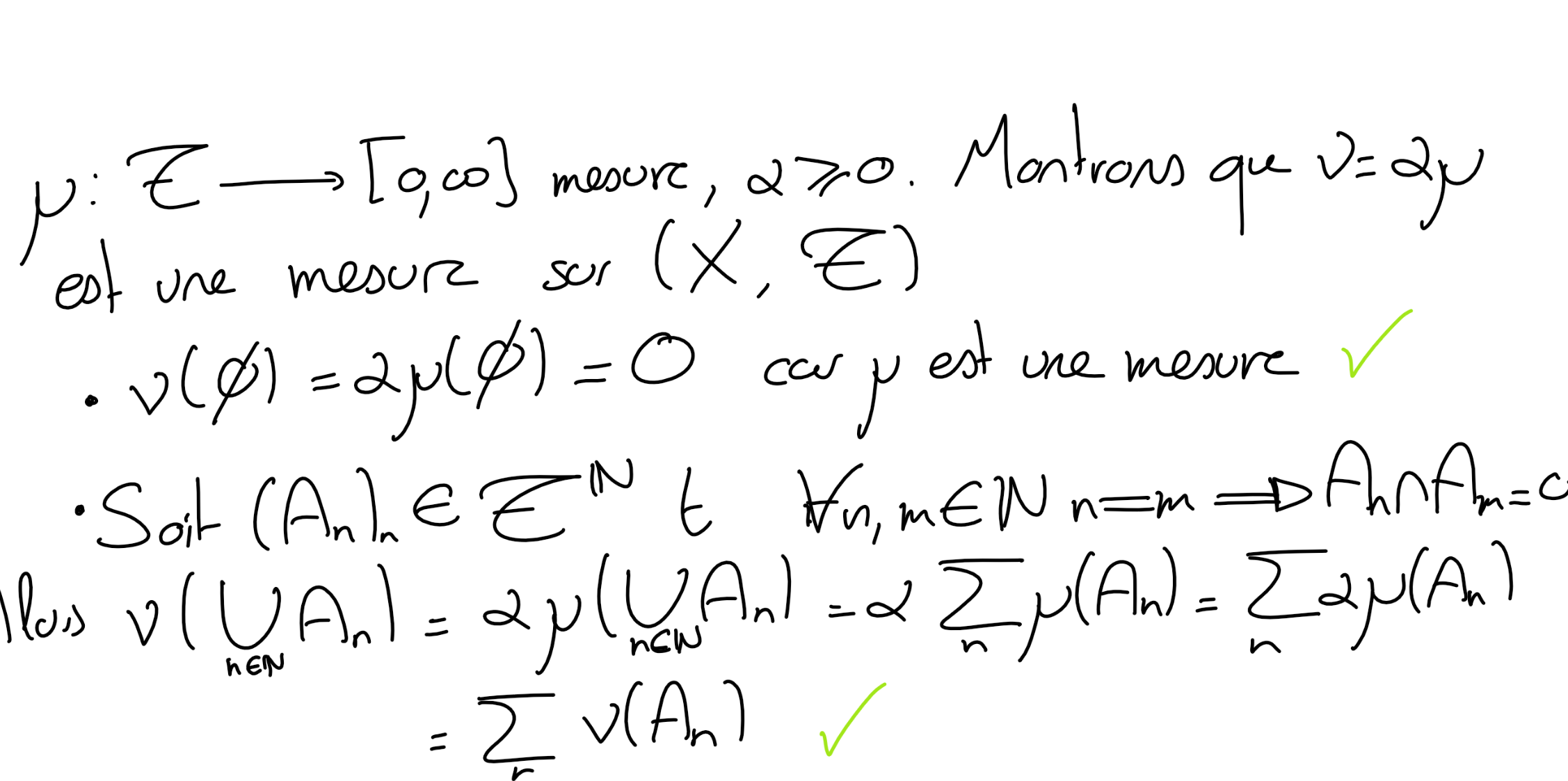Skip to main content

Section 4.2 Exemples de mesures

Exercice Mesure condtionnelle.

Soit \((X,\mathscr T,\mu)\) un espace mesuré, et soit \(B\in \mathscr T\) tel que \(\mu(B)\gt 0\text{.}\) Montrer que l'application:

\begin{align*} \mu(\,\cdot\, |B):\mathscr T \amp \rightarrow \rbb 0,\infty\lbb \\ A \amp \mapsto \frac{\mu(A\cap B)}{\mu(B)} \end{align*}

définit une mesure sur \((X,\mathscr T)\text{.}\)

Spoiler.

Exercice 4.2.1. La mesure de Dirac.

Soit \(X\) un ensemble, \(a\in X\text{,}\) on définit l'application

\begin{align*} \delta_a: \mathcal P(X) \amp \rightarrow \rbb 0,+\infty\lbb \\ A \amp \mapsto \begin{cases} 0 \text{ si } a\notin A\\ 1 \text{ si } a \in A \end{cases} \end{align*}

(a)

Montrer que \(\delta_a\) est une mesure sur \((X,\mathcal P(X))\text{.}\) On l'appelle mesure de Dirac en a 1 .

(b)

Montrer que \(\delta_a\) est une mesure finie.

Exercice 4.2.2. Somme de mesures et multiplication par une constante positive.

(a)

Soit \((X,\mathscr T, \mu)\) un espace mesuré, et soient \(\mu_1,\mu_2:\mathscr T \rightarrow \rbb 0,+\infty\lbb \) deux mesures sur \((X,\mathscr T, \mu)\text{.}\) Montrer que \(\mu_1+\mu_2\) est une mesure sur \((X,\mathscr T, \mu)\text{.}\)

(b)

Plus généralement, soit \((\mu_n)_n\) une suite de mesures positives sur \((X,\mathscr T, \mu)\text{.}\) Montrer que \(\mu=\sum_{n\in\N} \mu_n\) est aussi une mesure que \((X,\mathscr T, \mu)\text{.}\)

Spoiler.

(c)

Soit \((X,\mathscr T, \mu)\) un espace mesuré, \(\alpha \geq 0\text{.}\) Montrer que \(\nu = \alpha \mu\) est une mesure sur \((X,\mathscr T)\text{.}\)

Spoiler.

Armé de ces deux propriétés, on a donc:

Exercice 4.2.3. Mesure de comptage sur \((X, \mathcal P(X))\).

(a)

Montrer que l'application:

\begin{align*} \mu: \mathcal P(X)\amp \rightarrow \rbb 0,+\infty\lbb \\ A \amp \mapsto \begin{cases} \text{Card}(A) \text{ si } A \text{ fini,}\\ +\infty \text{ sinon.} \end{cases} \end{align*}

définit une mesure sur \((X, \mathcal P(X))\text{.}\)

Remarque: C'est la mesure qu'on utilise le plus souvent sur \((\N,\mathcal P(N))\text{,}\) et plus généralement sur les ensembles finis ou dénombrables  2 .

Spoiler.

(b)

Montrer que \(\mu = \sum_{n\in \mathbb N} \delta_n\text{.}\)
Spoiler.

(c)

Soit \((a_n)_n \in (\R^+)^\N\) une suite de réels positifs.

Montrer que

\begin{equation*} \mu_a : A\subset \N \mapsto \sum_{n\in\N}a_n\delta_n \end{equation*}

est une mesure sur \((\N,\mathcal P(\N))\text{.}\)

Montrer que \(\mu\) est \(\sigma\)-finie, et que \(\mu\) est finie ssi \((a_n)_n\) est le terme général d'une série convergente.

Spoiler.

Soit \(w:\mathbb N \rightarrow \rbb 0,+\infty\rbb \) une fonction positive. Montrer que l'application

\begin{equation*} \mu_w: E\in \mathcal P(\mathbb N) \mapsto \sum_{n\in E} w(n) \end{equation*}

définit une mesure sur \((\mathbb N,\mathcal P(\mathbb N)).\)

En particulier, si

\begin{equation*} w:n\in \mathbb N \mapsto \frac{\lambda^n}{n!}e^{-\lambda}, \end{equation*}

on obtient une mesure de probabilité: la loi de Poisson sur \(\mathbb N\text{.}\)

En fait, toutes les mesures sur \((\mathbb N, \mathcal P(\mathbb N))\) peuvent s'exprimer de manière similaire:

Montrer que si \(\mu\) est une mesure sur \((\mathbb N, \mathcal P(\mathbb N))\text{,}\) alors il existe une suite \((u_n)_n\in (\overline R_+)^\mathbb{N}\) telle que

\begin{equation*} \mu = \sum_{n\in \mathbb N}u_n\delta_n \end{equation*}
Spoiler.
Parenthèse culturelle: l'idée de la mesure de Dirac a des ancêtres dans les travaux de Fourier et Cauchy, et représente, en physique, une charge électrique ou une masse concentrée en un seul point. La notation \(\delta_p\) fut introduite par le physicien Paul Dirac, un des fondateurs de la mécanique quantique, comme une généralisation ``continue'' des symboles de Kronecker \(\delta_{ij}\text{.}\)
En anglais, ces ensembles s'appellent "countable sets". Ceux qu'on peut compter, donc. D'où l'idée...de compter.