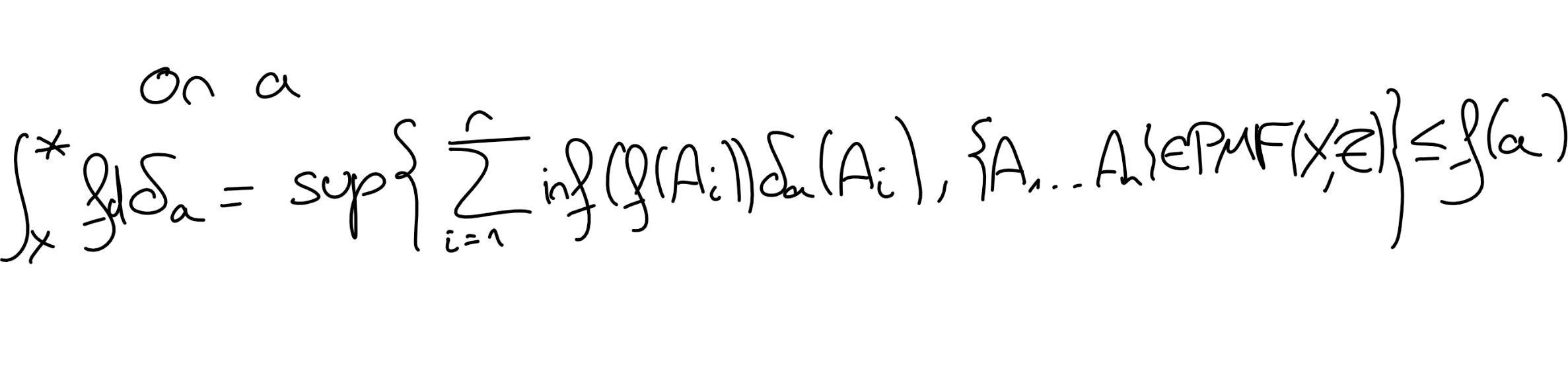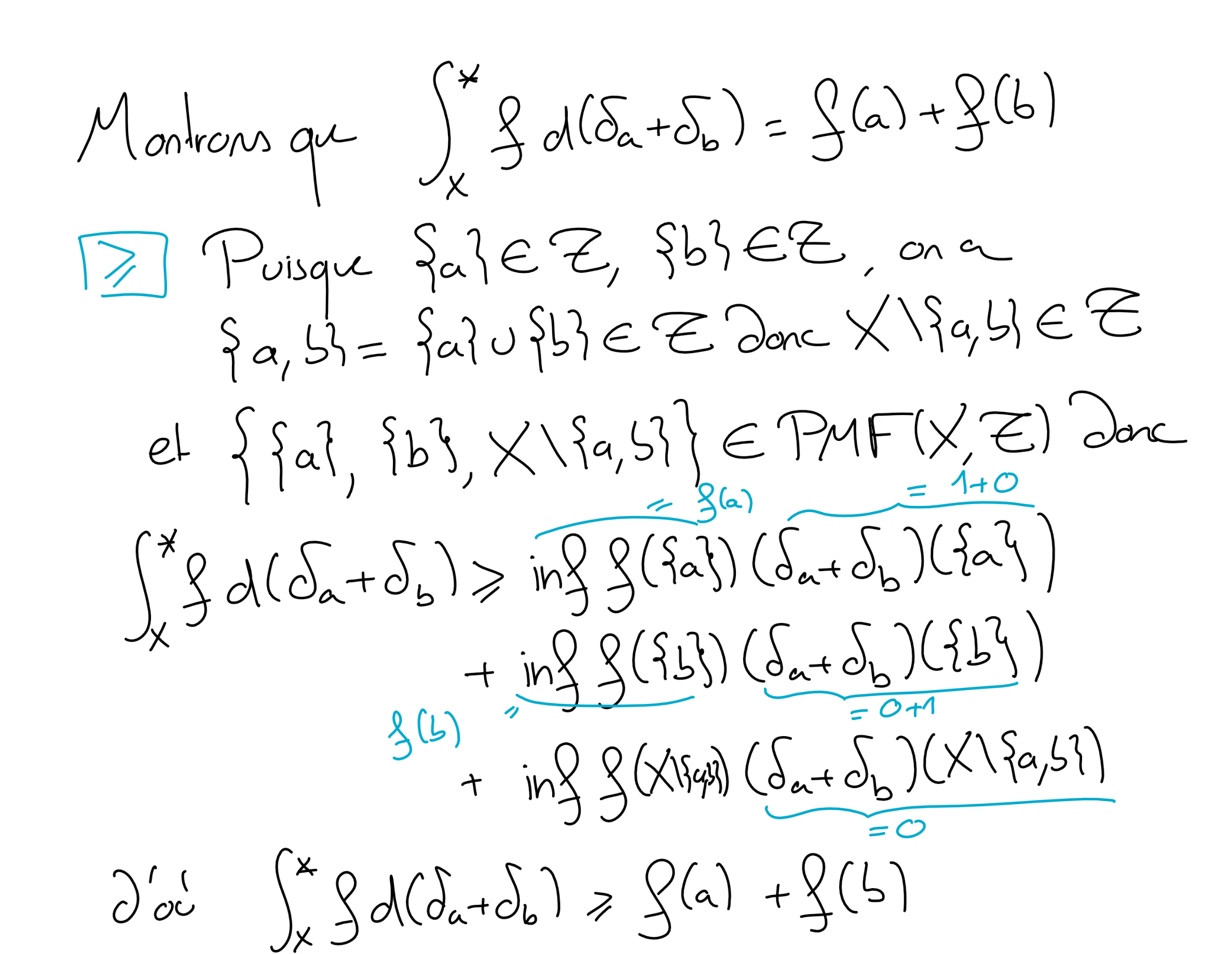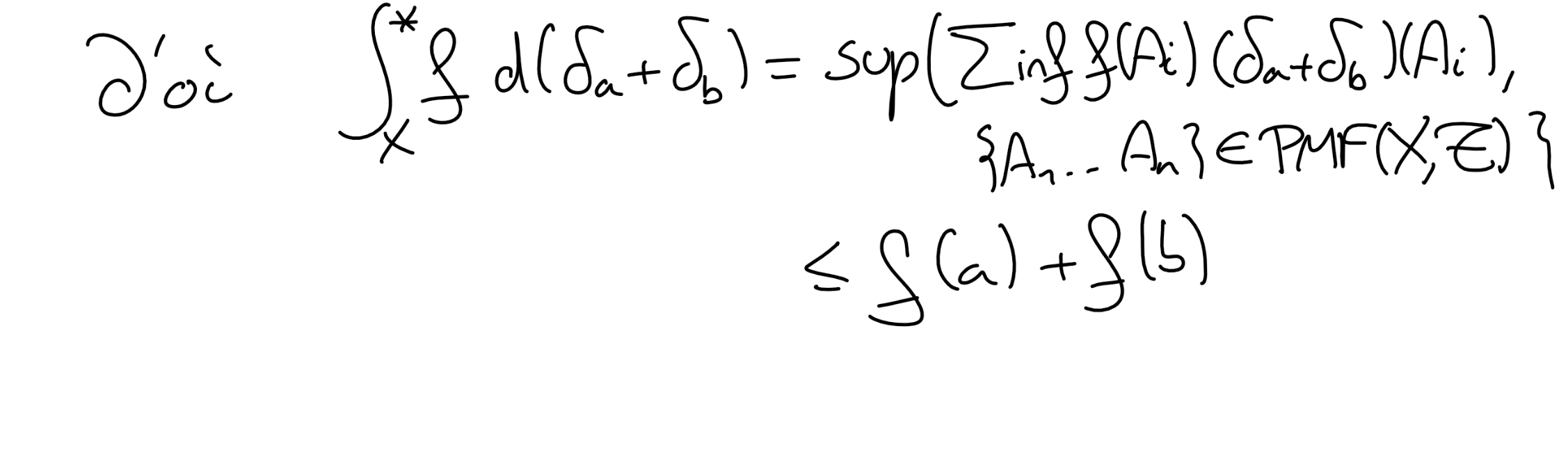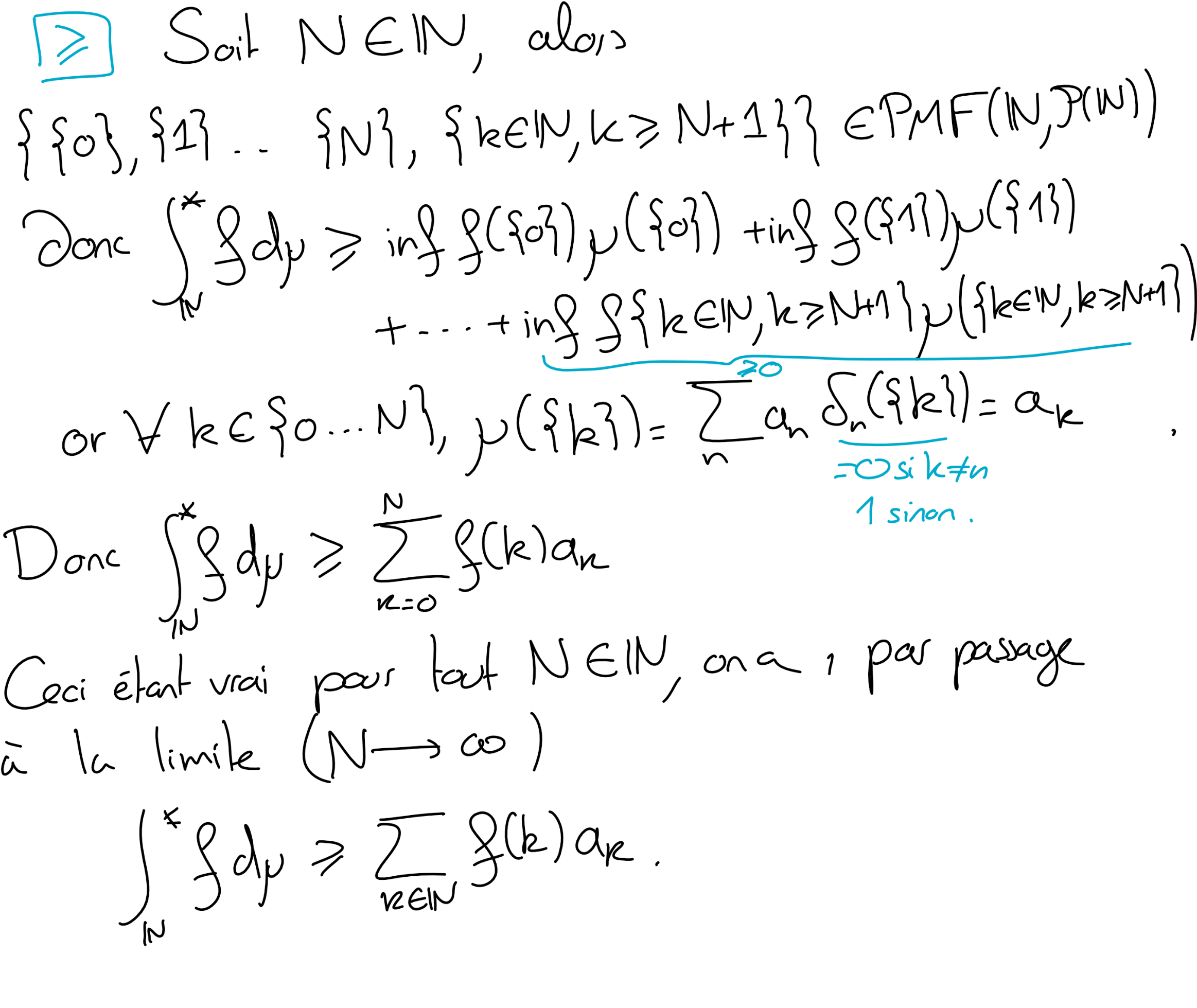Exemples de calculs d'intégrales

Section 7.4 Exemples de calculs d'intégrales

Exercice 7.4.1. Intégration par rapport à la masse de Dirac.

(a)

Soit \((X,\mathscr T)\) un ensemble mesurable, \(a\in X\) tel que \(\{a\} \in \mathscr T\text{.}\) On munit \((X,\mathscr T)\) de la mesure de Dirac \(\delta_a\) en \(a\) (voir Exercice 4.2.1). Soit \(f\in \mathcal L^0((X,\mathscr T), (\rbb 0,+\infty\lbb , \mathscr B(\rbb 0,+\infty\lbb )))\text{.}\) Montrer que

\begin{equation*} \int_X^* fd\delta_a = f(a) \end{equation*}

Indice.

Procéder par double inégalité: puisque la définition de l'intégrale supérieure fait intervenir un sup, c'est plus pratique.

Spoiler.

(b)

Soit \(b\in X\) un autre point tel que tel que \(\{b\} \in \mathscr T\text{.}\) Montrer que

\begin{equation*} \int_X^* fd(\delta_a+\delta_b) = f(a)+f(b) \end{equation*}

Indice.

Pour l'une des inégalités, il peut être utile de considérer une PMF \(\{A_1,\ldots,A_n\}\) de \((X,\mathscr T)\text{,}\) et de séparer les cas selon si \(a\) et \(b\) sont dans le même \(A_{i_0}\) ou dans deux \(A_i\) différents.

Spoiler.

Exercice 7.4.2. Intégrales sur \(\mathbb N\).

(a)

Soit \((a_n)_n \in (\mathbb R_+)^{\mathbb N}\) une suite de réels positifs, on considère la mesure sur \((\mathbb N, \mathcal P(\mathbb N))\) définie par

\begin{equation*} \mu =\sum_{n\in \mathbb N}a_n \delta_n. \end{equation*}

Soit \(f\in \mathcal L^0(\mathbb N, \mathcal P(\mathbb N);\overline{\mathbb R}_+)\text{.}\) Montrer que

\begin{equation*} \int_{\mathbb N}^* fd\mu= \sum_{n\in\mathbb N} a_n f(n). \end{equation*}

Spoiler.

(b)

On a vu à l'Exemple 4.2.1 que, si \(w:\mathbb N \rightarrow \rbb 0,+\infty\rbb \) une fonction positive, alors \(\mu_w: E\in \mathcal P(\mathbb N) \mapsto \sum_{n\in E} w(n)\) définit une mesure sur \((\mathbb N, \mathcal P(\mathbb N))\text{.}\)

Soit \(f: \mathbb N \rightarrow \rbb 0,\infty\lbb \text{.}\) Montrer que

\begin{equation*} \int_{\mathbb N} f d\mu_w = \sum_{n\in\mathbb N}f(n)w(n) \end{equation*}